UNE FORTUNE SUR UN ECHIQUIER

Posons 1 centime sur la première case d'un échiquier, 2 sur la case suivante, puis 4, puis 8 et ainsi de suite en doublant chaque fois la mise.

Question : Combien possèderons-nous sur la dernière case ?

Réponse : A partir de la deuxième case on doublera 63 fois le contenu de la case précédente. Ce qui donnera sur la dernière case 2 puissance 63 soit 9 milliards de milliards de centimes. Même en centimes, le total est plus que tout l'argent du monde !

UN TRES GRAND NOMBRE : L'INFINI

Le mathématicien David de Hilbert inventa un hôtel imaginaire pour représenter l'infini mathématique. Supposons qu'il y ait une infinité de chambres dans cet hôtel, mais toutes occupées. Un client se présente et demande une chambre. Le propriétaire réfléchit une minute puis demande à tous les occupants de déménager dans la chambre voisine. Le client de la chambre 1 s'installera dans la chambre 2, celui de la chambre 2 dans la 3, etc. Le nouveau client aura ainsi sa chambre.

Le lendemain arrive un bus infiniment long rempli d'un nombre infini de nouveaux clients. Le propriétaire demande alors à tous les occupants de déménager dans la chambre dont le numéro est le double de la leur. Ils s'installeront ainsi tous dans une chambre portant un numéro pair, et l'infinité des chambres portant un numéro impair deviendra libre.

LA CELEBRE SUITE DE LEONARDO FIBONACCI

Regardez bien cette suite imaginée par le mathématicien italien Leonardo Fibonacci (né en 1175 à Pise) : chaque terme de cette suite est la somme des deux termes précédents.

Habituellement, les marguerites ont 34, 55 ou 89 pétales. Ces nombres appartiennent à la série de Fibonacci. Il en est de même pour le tournesol. Le nombre de pétales d'une fleur est très souvent un terme de la série de Fibonacci. En comptant le nombre de branches d'un arbre autour du tronc sur un tour complet (en décrivant une hélice) on tombe souvent sur un terme de la série de Fibonacci. Il en est de même du nombre de spirales des pommes de pin, des brocolis, des choux-fleurs ou de l'écorce des ananas.

POURQUOI ? Certainement parce que les nombres de la série de Fibonacci fournissent aux graines, aux pétales, aux feuilles, aux branches, ... le meilleur moyen d'utiliser l'espace, sans trop d'écarts et sans se chevaucher.

1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, ...

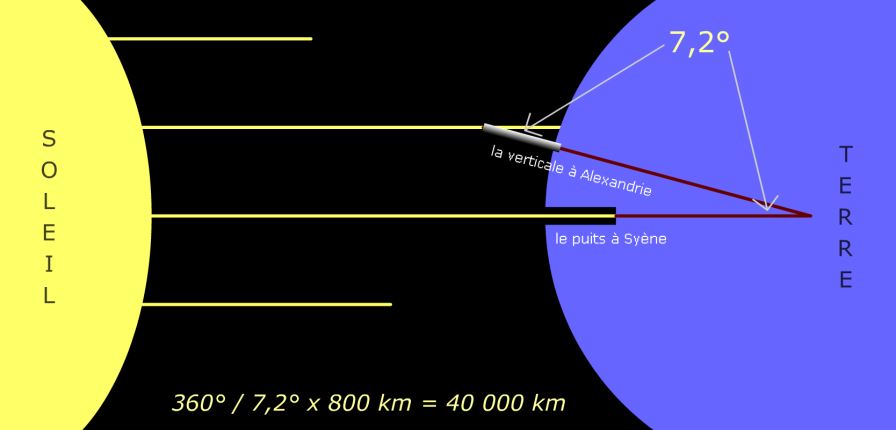
LA CIRCONFERENCE DE LA TERRE EN 250 AVANT JC

Vers 250 avant Jésus-Christ, Eratosthène (mathématicien et philosophe égyptien) avait entendu dire que le jour du solstice d'été le jour le plus long de l'année) à Syène (Assouan), au sud de l'Egypte, les rayons du Soleil parvenaient à toucher le fond d’un puits étroit et profond à midi.

Le même jour à Alexandrie, situé à 5 000 stades (800 km) au nord de Syène, il mesura l'angle que faisaient les rayons du Soleil avec la verticale. Il mesura un angle de 7,2 degrés qu'il attribua à la courbure de la Terre. Comme 7,2 est un cinquantième de 360 degrés, il multiplia la distance entre Syène et Alexandrie par 50 et détermina la circonférence de la Terre (40 000 km). VOIR L'ILLUSTRATION CI-DESSUS.

KARL GAUSS CALCULAIT TRES VITE !

Combien fait la somme des nombres de 1 à 100 ?

Karl Gauss (1777-1855) avait ajouté le premier et le dernier nombre (1+100) ce qui fait 101. Puis le deuxième et l'avant-dernier (2+99) ce qui donne également 101. Il comprit qu'il pouvait procéder de cette manière 50 fois. La réponse est donc :

           la somme des nombres de 1 à 100 = 50 x 101 = 5 050

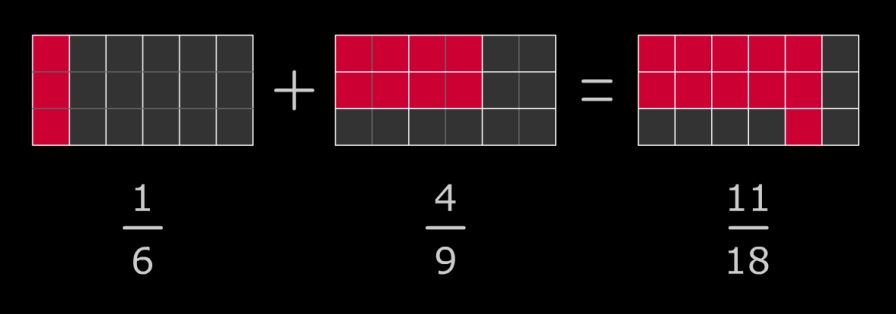
L'ALGEBRE GEOMETRIQUE

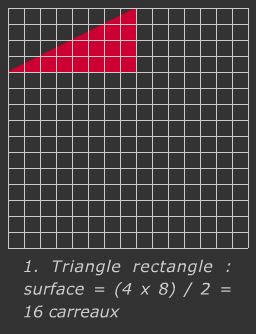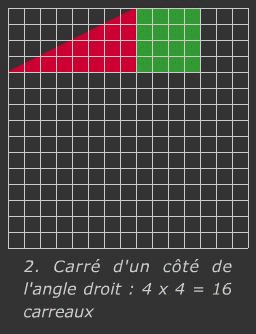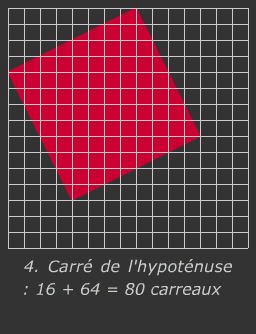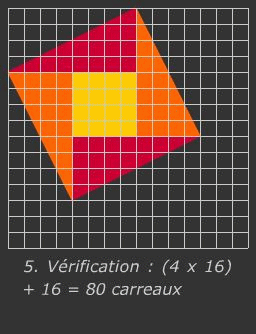
A titre pédagogique, dans l'antiquité, les grecs utilisaient des méthodes géométriques pour faire des calculs. Voyez ci-dessus l'exemple de l'addition de 2 fractions n'ayant pas le même dénominateur.

Et voyez ci-contre une démonstration par la géométrie du Théorème de Pythagore. Rappel du théorème : Dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des côtés de l’angle droit.