

 page créée le 15 juillet 2017 et modifiée le 11 novembre 2018
page créée le 15 juillet 2017 et modifiée le 11 novembre 2018
Le but de cette page est de comprendre ce que signifie E = mc² et ce qu'on peut découvrir derrière cette formule.
Pour bien appréhender cette célèbre formule d'Albert EINSTEIN (1879-1955), voici les 9 différentes sections, en 2 parties (les bases et les fondamentaux), qui seront abordées dans cette page (c'est la progression pédagogique que je propose):
PARTIE I (les bases)
1. MASSE et POIDS
2. VITESSE DE LA LUMIÈRE
3. PARTICULES
4. ÉNERGIE CINÉTIQUE
5. ÉNERGIE DE MASSE ... ou ... E = mc²
6. ÉNERGIE CINÉTIQUE + ÉNERGIE DE MASSE
7. LES FORCES NUCLÉAIRES
8. CONCLUSION
PARTIE II (les fondamentaux)
9. DERNIÈRE QUESTION
AVERTISSEMENT: cette page n'est pas un copié-collé d'articles trouvés sur Internet ou ailleurs (cela aurait si peu d'intérêt). Seuls certains documents photographiques ont été récupérés sur la toile. J'ai voulu comprendre ce que signifiait E=mc² et mon but fut alors de développer cette page y rassembler mes éléments d'analyse. Cependant, en lisant ce qui suit, vous constaterez peut-être des inexactitudes et je vous invite à ne pas hésiter à me transmettre vos remarques ou corrections nécessaires (rappel de mon adresse électronique: gilles.febvrel@gmail.com).
1

1 . M A S S E E T P O I D S
Il ne faut pas confondre masse et poids. Saviez-vous que le poids est égal à la masse multiplié par la gravitation (unité d'accélération)? Cela s'écrit ainsi: P = mg. Ce n'est pas compliqué et comme une image vaut mieux que mille mots, je vous propose trois dessins que j'ai réalisés.
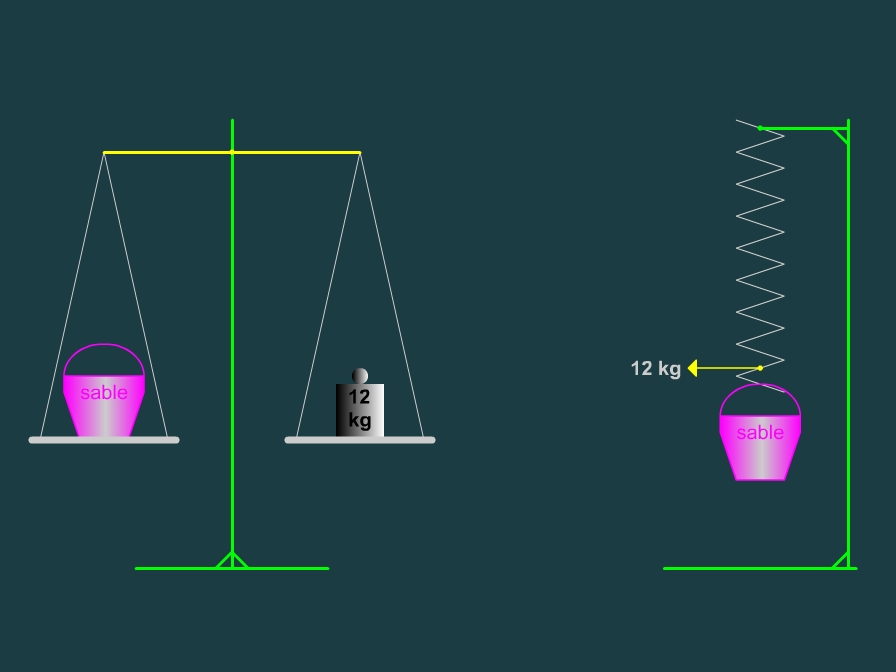
Ci-dessous: nous sommes sur Terre et nous pesons un seau rempli de sable avec une balance à poids (une balance à colonne) et une balance à ressort (un dynamomètre).
Nous voyons dans les deux pesées que le seau rempli de sable pèse 12 kilogrammes. C'est normal.
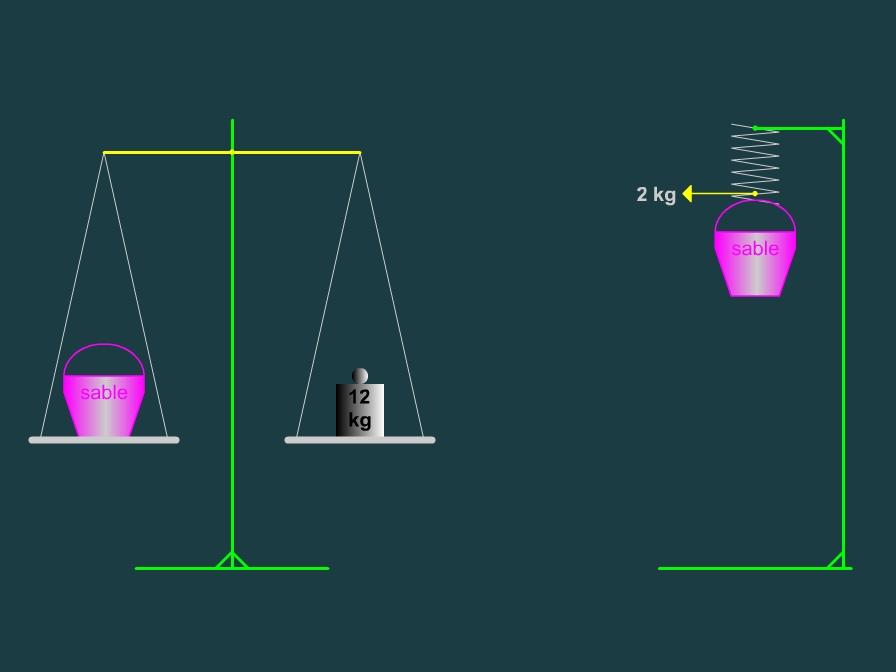
Je vous propose maintenant de prendre les deux balances, le seau de sable et le poids de 12 kilogrammes et d'aller sur la Lune. Regardez ce qui se passe sur le dessin ci-dessous.
On constate, sur la Lune, que notre seau rempli de sable pèse toujours 12 kilogrammes sur la balance à colonne. Mais le même seau affiche 2 kilogrammes sur le dynamomètre. Et là aussi c'est normal car le dynamomètre tient compte d'un facteur dont se "moque" la balance à colonne: la pesanteur. La Lune étant plus petite que la Terre, sa force gravitationnelle est six fois moindre. Le dynamomètre affiche donc 2 kilogrammes (12/6).
Aussi, les 12 kilogrammes constatés sur la pesée avec la balance à colonne représentent la MASSE du seau rempli de sable. LA MASSE EST STABLE ET INVARIABLE quelque soit son référentiel (Terre, Lune, Mars, espace loin de tout objet céleste, ...).
La masse a comme unité le kilogramme.
Le POIDS, quant à lui, VARIE EN FONCTION DE LA GRAVITATION et a comme unité le newton (N). (Pour information: 1 newton est la force capable de communiquer à une masse de 1 kilogramme une accélération de 1 mètre par seconde au carré (note: il s'agit de seconde au carré et non pas de seconde car il est ici question d'accélération et non pas de vitesse). Pour des raisons pédagogiques le dynamomètre de mon dessin affiche des kilogrammes alors qu'il devrait afficher des newtons. Les 12 kilogrammes, masse du seau rempli de sable, font 117,67 newtons sur la Terre et 19,61 newtons sur la Lune, soit six fois moins.
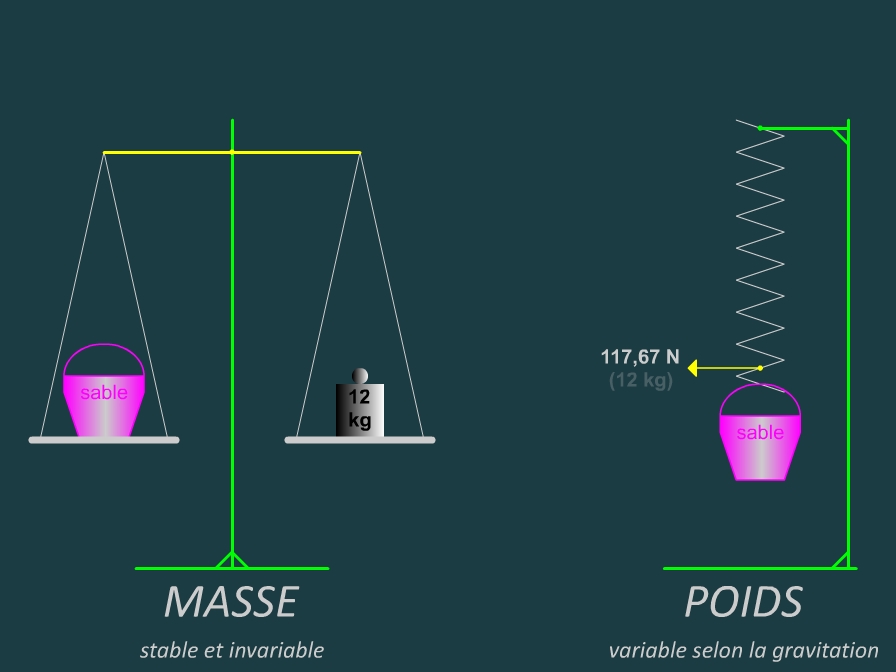
Conclusion:
Quand nous parlons de poids dans la vie courante (celui que nous lisons sur un pèse-personne par exemple) nous devrions parler de masse. Ce n'est pas très grave de parler de poids au lieu de masse dans la vie quotidienne mais en physique il y a lieu de ne pas confondre masse et poids.
Je vous disais au début de cette section que P = mg (Poids = masse multiplié par la gravitation). La gravitation (g) sur la Terre est égale à 9,81 newtons pour 1 kilogramme. Si nous multiplions les 9,81 newtons par la masse du seau rempli de sable (12 kilogrammes) nous obtenons bien les 117,67 newtons qu'affiche le dynamomètre sur la Terre. Voir le dessin ci-dessous.
2

2 . V I T E S S E D E L A L U M I È R E
Avant de parler de la vitesse de la lumière, il est bon de rappeler que la lumière est un ensemble d'ondes visibles par l'oeil humain. Pourquoi un ensemble d'ondes? Car une onde se caractérise par sa longueur (*) et qu'à chaque longueur d'onde correspond une des sept couleurs fondamentales: le violet, l'indigo, le bleu, le vert, le jaune, l'orangé et le rouge.
Note (*): tout à la fin de cette page je propose une explication plus approfondie sur les ondes de la lumière. Cependant, ces explications ne sont pas indispensables pour comprendre la suite du sujet traité dans cette page.
Dans le vide, la vitesse de la lumière est de 299 792 458 mètres par seconde. Ce qui fait, en arrondissant un peu, 300 mille kilomètres par seconde.
A titre d'exemple, pour parcourir les 150 millions de kilomètres qui nous séparent du Soleil, sa lumière met 8 minutes et 22 secondes pour arriver à la surface de la Terre.
Autre exemple: à certains endroits de Toulouse on peut voir, par temps clair, la cime des Pyrénées qui est à 60 kilomètres plein sud. L'image des sommets enneigés (en toute saison) met un cinq millième de seconde pour arriver à nos yeux.
Note: pour les très longues distances on utilise une unité appelée année-lumière (al). Une année-lumière est la distance que parcourt dans le vide la lumière en une année. Ce qui représente 10 000 milliards de kilomètres. En conséquence, une lumière située à une année-lumière de la Terre mettra une année pour arriver sur la surface de la Terre.
Dernier exemple: si aujourd'hui (en 2018) se produit dans l'univers une supernova (c'est l'explosion d'une étoile avec dégagement très important de lumière avant son extinction totale) située à 2 000 années-lumière de la Terre, elle sera observable à l'oeil nu depuis le plancher des vaches en 4018: on verra alors sa forte luminosité et son extinction alors que l'étoile n'existe déjà plus depuis longtemps (depuis 2 000 ans).
Avant de conclure cette section sachez que la vitesse de la lumière est symbolisée par la lettre c, c comme célérité (en physique, la célérité est la vitesse d'une onde).
3

3 . P A R T I C U L E S
La matière qui nous entoure, quelle soit vivante (un humain, un arbre, une fleur, un poisson, ...) ou quelle soit inerte (une pierre, un verre, une chaise, ...) est constituée d'atomes.
Un atome à la taille d'un millimètre divisé par dix milliards (soit 0,0000000001 millimètre).
Les atomes sont regroupés en molécules (*).
(*) Note: Les molécules comprenant du carbone sont également appelés molécule organique ou plus fréquemment composé organique. Le carbone est un atome très répandu. Par exemple, près de 99% de la masse du corps humain sont représentés par seulement six éléments: l'oxygène, le carbone, l'hydrogène, l'azote, le calcium et le phosphore.
Pour les matières vivantes, et seulement pour celles-là, les molécules sont, en plus, regroupées en cellules.
Il existe, à ce jour, 118 atomes dans l'univers, du plus léger (l'hydrogène) au plus lourd (l'uranium) en passant par le fer, le cuivre, le zinc, l'argent, etc. Sachez également que l'on utilise très souvent l'expression "élément chimique" à la place du mot "atome".
Un atome (ou un élément chimique) est constitué d'un noyau autour duquel gravitent des électrons. Le noyau est composé de protons et de neutrons. Il y a toujours le même nombre de protons que d'électrons. Ce nombre variant d'un atome à l'autre (ainsi que le nombre de neutrons). Exemples:
- 1 atome d'hydrogène comprend 1 proton, 1 électron et aucun neutron,
- 1 atome d'oxygène comprend 8 protons, 8 électrons et 8 neutrons,
- 1 atome d'uranium comprend 92 protons, 92 électrons et 146 neutrons.
L'eau est une matière composée de molécules. Chaque molécule d'eau comprend 2 atomes d'hydrogène et 1 atome d'oxygène.
Les électrons, protons et neutrons sont des PARTICULES (*).
(*) Note: En réalité les protons et les neutrons renferment des particules appelées quarks. Elles sont indissociables. On ne peut pas les séparer.
Les particules sont si petites que l'espace vide entre le noyau et les électrons est grand (comparativement). Un atome est donc essentiellement constitué de vide. Les électrons se déplacent dans ce vide à la vitesse de la lumière. Si un atome était grand comme un terrain de football, le noyau de cet atome serait un petit pois posé quelque part au centre de ce terrain.
Voici un petit dessin que j'ai réalisé pour tout résumer (une image vaut mieux que mille mots):
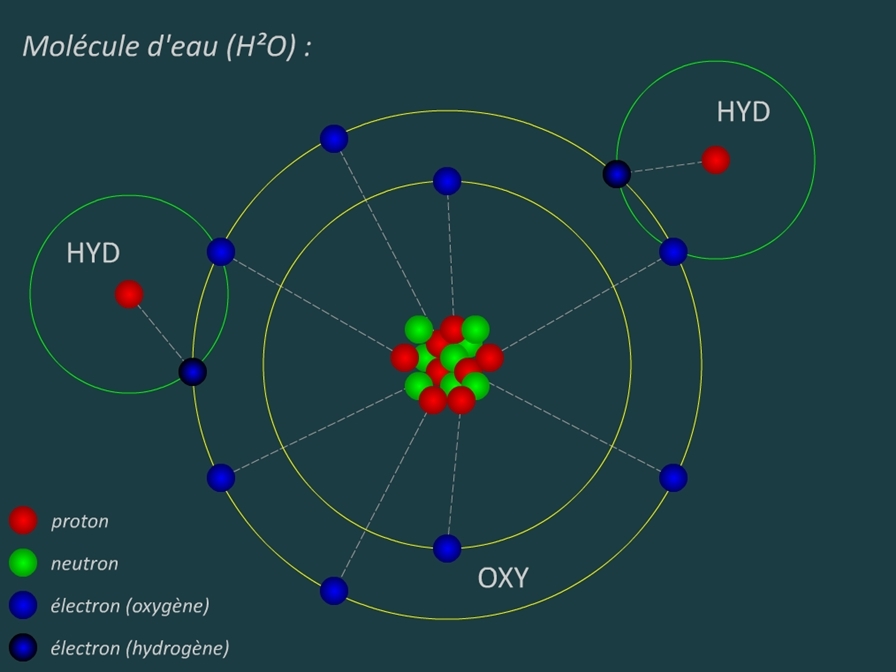
Note: le dessin (ci-dessus) montre bien les 8 protons et les 8 neutrons du noyau de l'atome d'oxygène ainsi que les 8 électrons "associés" à ce noyau. On voit également les 2 atomes d'hydrogène qui comprennent qu'un seul proton dans le noyau (et aucun neutron) et un électron. IMPORTANT: les 2 atomes d'hydrogène sont liés à l'atome d'oxygène du fait que l'électron de chacun des atomes de l'hydrogène croise l'orbite de l'atome d'oxygène. C'est ainsi que l'association hydrogène (2 atomes) et oxygène (1 atome) est constituée dans une molécule d'eau.
Pour conclure cette section dédiée aux particules, il est bon de se rappeler pour la suite de cette page, que la matière est constitué d'atomes dans lesquels il y a des particules qui se déplacent dans le vide à la vitesse de la lumière.
4

4 . É N E R G I E C I N É T I Q U E
Pour être le plus clair possible, je vous propose de définir ce qu'est l'énergie cinétique par un exemple concret: imaginez une voiture circulant à grande vitesse sur une autoroute. Si nous coupons soudainement l'énergie de la voiture (sans plus accélérer du tout, par exemple, et sans freiner) la voiture va continuer à rouler. Cette énergie porte le nom d'ÉNERGIE CINÉTIQUE. Elle correspond d'ailleurs exactement à l'énergie nécessaire pour stopper la voiture.
L'énergie cinétique est la quantité de travail que peut produire un corps par suite du mouvement dont il est animé.
Il n'est pas difficile de comprendre que l'énergie cinétique de la voiture de notre exemple ci-dessus dépendra de sa masse (en kilogrammes) et de sa vitesse. En effet, plus le véhicule sera lourd et sa vitesse importante, plus son énergie cinétique sera grande.
On pourrait donc écrire que l'énergie cinétique (Ec) est égale à la masse (m) multipliée par la vitesse (v).
C'est presque juste car en réalité nous devons considérer le demi-produit de la masse avec le carré de la vitesse.
On aura donc:
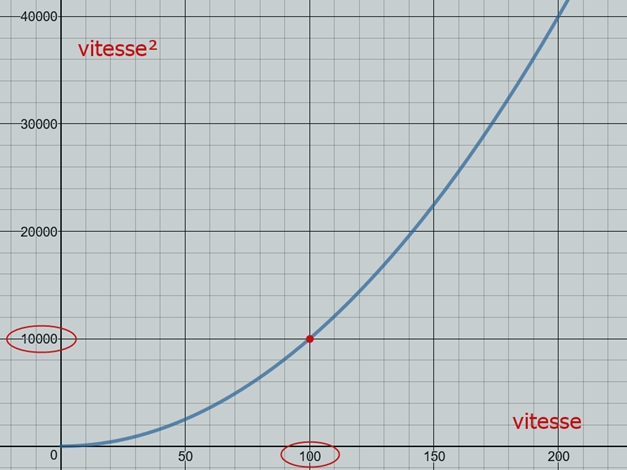
Note: la vitesse est portée au carré dans cette formule car (exemple) une bille en acier projetée à 50 km/h dans un mur en terre glaise s'enfoncera dans celui-ci et la même bille projetée dans les mêmes conditions à une vitesse de 100 km/h ne s'enfoncera pas deux fois plus profondément mais quatre fois plus. L'impact est exponentiel (voir la courbe de v² ci-dessous) et non pas linéaire. Autre approche pour bien comprendre: il faudra 4 fois plus d'énergie pour lancer un objet à 20 km/h qu'à 10 km/h. En conséquence, réduire la vitesse de moitié c'est diviser par quatre son énergie cinétique. Et enfin cet autre exemple: la distance de freinage d'un véhicule croît plus rapidement que la vitesse du véhicule (si ce véhicule roule 3 fois plus vite alors sa distance de freinage sera 9 fois (3 au carré) plus longue). Quant à la division par 2, elle trouve son origine dans les équations initiales d'où découle la formule.
Exemple concret d'un calcul d'énergie cinétique:
Note préalable: l'unité utilisée pour quantifier Ec s'appelle JOULE , et ...
- comme m est la masse qui s'exprime en kilogramme,
- comme v est la vitesse qui s'exprime en mètres par seconde,
- mv² donneront des kilogrammes mètre carré par seconde au carré,
- et donc 1 joule = 1 kilogramme mètre carré par seconde au carré.
Quelle est l'énergie cinétique d'un camion d'une tonne qui roule à 100 km/h?
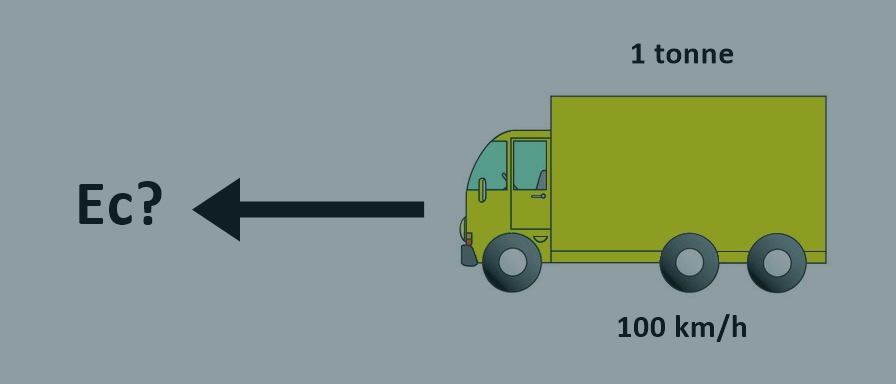
• en physique, la vitesse s'exprime en mètres par seconde (m/s):
- 1 heure --> 1 kilomètre
- 3600 secondes --> 1 kilomètre
- 3600 secondes --> 1000 mètres
- 1 seconde --> 1000 / 3600 = 0,28 mètre
- conclusion: 1 km/h = 0,28m/s
- exemple: 100 km/h = 0,28 x 100 = 28 m/s
• dans la formule Ec = ( m x v² ) / 2, l'énergie cinétique Ec s'exprime en joules (c'est-à-dire en kilogramme mètre carré par seconde au carré),
• on sait que 100 km/h = 28 m/s (voir ci-dessus),
• on sait que 1 tonne = 1000 kg,
• appliquons la formule: Ec = (1000 × (28)²) / 2 = 392000 Joules = 392 Kilojoules,
• l'énergie cinétique développée par un camion d'une tonne à 100 km/h est donc de 392 kJ.
AUTRES EXEMPLES:
• Une balle de tennis qui a une masse de 58 grammes (0,058 kg) développe à la vitesse de 200 km/h (56 m/s) une énergie de 91 Joules.
• Un ballon de football qui a une masse de 450 grammes (0,45 kg) développe à la vitesse de 150 km/h (42 m/s) une énergie de 397 Joules. À 50 km/h (14 m/s) ce ballon de football développerait une énergie de 44 Joules.
Pour conclure cette section dédiée à l'énergie cinétique, il est bon de rappeler, pour la suite de cette page, que la formule "Ec = mv² /2" permet de CONVERTIR UNE VITESSE EN ÉNERGIE.

5

5 . E = m c 2
Avant de poursuivre sachez que tout ce qui a une masse est de la matière. Et par le terme "matière", comprenez tout ce qui compose les corps qui nous entourent, c'est-à-dire tout ce qui a une masse et un volume.
Une pierre posée sur le sol ne dégagera aucune énergie cinétique car cette pierre n'est pas en mouvement.
Si cette pierre est lancée par un humain, projetée par une explosion ou si elle subit une chute due à un éboulement, cette pierre dégagera une énergie cinétique car elle sera en mouvement.
Une pierre (ou une roche) est un matériau de l'écorce terrestre. C'est habituellement un solide composé d'un assemblage de minéraux. Comme toute matière, un minéral est un assemblage d'atomes. Dans la section PARTICULES de cette page on a vu qu'un atome est un noyau autour duquel gravitent des électrons qui se déplacent à la VITESSE DE LA LUMIÈRE.
Sachant que l'on peut convertir de la vitesse en énergie (voir la précédente section), sachant que la vitesse de la lumière est de 300 millions de mètres par seconde et en considérant, par exemple, 1 grain de sable (extrait de notre roche) de 1 gramme, nous pouvons calculer (en appliquant la formule E=mc² où "E" est l'énergie, "m" est la masse et "c" est la célérité c'est-à-dire la vitesse de la lumière):
a) le carré de la vitesse de la lumière:
• (300 000 000 m/s) au carré = (3 x 10 puissance 8) au carré = (9 x 10 puissance 16) m2/s2
b) le produit de la masse (1 gramme) avec la vitesse au carré:
• 1 gramme = (1 x 10 puissance -3) kilogramme = 0,001 kg
• 0,001 kg x (9 x 10 puissance 16) m2/s2 = (9 x 10 puissance 13) joules
L'énergie contenue dans un grain de sable de 1 gramme est donc de 90 000 000 000 (90 milliards) de kilojoules, ce qui est CONSIDÉRABLE!
On peut dire qu'un grain de sable d'un gramme projeté à 100 km/h développera une énergie cinétique de 0,39 joules; ce même grain contenant par ailleurs (et en permanence) une énergie interne de 90 milliards de kilojoules.
Cette énergie interne est appelée énergie de masse, alors que celle développée par le déplacement d'un objet est appelée énergie cinétique.
ÉNERGIE CINÉTIQUE (une automobile en mouvement)

ÉNERGIE DE MASSE (un grain de sable inerte)

Énergie de masse:
L'énergie de masse d'un objet est une énergie interne considérable qui devient apparente à condition de "casser" le noyau de l'atome. Nous verrons dans une section ci-dessous que la fission (action de fendre, de casser) de l'atome est le processus utilisé dans les bombes atomiques et dans les centrales nucléaires. On verra également que la fission de l'atome peut être un phénomène naturel observé dans les étoiles (dans l'étoile Soleil, par exemple).
• Attention: la combustion (du bois par exemple) n'est pas une fission de l'atome et n'entraîne donc pas une "libération" de l'énergie de masse contenu dans la matière que l'on brûle. La combustion entraîne une réaction chimique au cours de laquelle se produit un transfert d'électrons et qui porte le nom de réaction d'oxydoréduction.
• Exemple du bois: le bois est principalement constitué d'atomes de carbone, d'hydrogène et d'oxygène. Il y a aussi d'autres éléments. Quand quelque chose brûle, les atomes se combinent avec l'oxygène dans l'air. Le carbone devient du dioxyde de carbone, l'hydrogène devient de l'eau et les atomes d'oxygène deviennent des molécules d'oxygène. Ce sont tous ces gaz qui, mélangés avec l'air, donnent l'impression que le bois disparaît.
• Loi fondamentale de << conservation des masses >>: la masse peut être considérée comme la quantité de matière dans un objet. La loi de << conservation des masses >> affirme que la masse est toujours conservée. Autrement dit, quoique que nous faisons avec la matière, telle un système fermé, nous aurons toujours la même quantité de substance à la fin. Par exemple, si nous brûlons une bûche, le bois deviendra plus léger car le "carburant" qu'il contient est utilisé. Cependant, si nous rassemblons les cendres, toutes les petites particules de fumée et la vapeur d'eau produite par le processus de combustion, et que nous pesons le tout, nous constaterons que la masse est exactement égale à la masse de la bûche qui a brûlé. Autrement dit: même après combustion, la somme des masses des matières (cendres, fumée, vapeur d'eau, ...) sera strictement égale aux masses des matières de la bûche avant qu'on la brûle. Déjà, Antoine LAVOISIER (1743-1794), chimiste, philosophe et économiste français, avait confirmé que << rien ne se perd, rien ne se crée, tout se transforme >>.
• Dernier exemple pour bien matérialiser la loi fondamentale de << conservation des masses >>: l'eau en gelant augmente de volume mais sa masse ne change pas. Faites l'expérience: vous mettez 1 litre d'eau liquide dans votre congélateur (1 litre d'eau pèse 1 kilogramme). Vous aurez donc mis dans le congélateur un volume de 1 litre d'eau (liquide) qui fait une masse de 1 kilogramme. Le lendemain vous constaterez que le bloc d'eau gelé fait toujours un poids de 1 kilogramme mais que son volume a augmenté et fait maintenant 1,1 litres (soit 10% de plus, ... environ). En conséquence, dans un volume de 1 litre, le poids de l'eau gelé sera inférieur au poids de l'eau liquide ... et ceci explique pourquoi les glaçons ou les icebergs flottent.

6

6 . É N E R G I E C I N É T I Q U E + É N E R G I E D E M A S S E
Une boule de 15 kilogrammes est posée sur une table (ci-dessous, image de gauche) ...
• son énergie cinétique est nulle: 0 joule,
• son énergie de masse est très importante: 15 mille fois le grain de sable de l'exemple ci-dessus.
La boule chute sur le sol (ci-dessous, image de droite) ...
• son énergie cinétique n'est plus nulle et fait: 147 joules (*),
• son énergie de masse demeure inchangée et fait donc: 15 mille fois 90 milliards de kilojoules.
(*) Note: pour calculer les 147 joules on a appliqué la formule Ec = mv²/2 où la vitesse est, dans notre exemple, celle de la chute d'un corps. La formule pour calculer la vitesse d'un corps en chute libre est la racine carrée du double de la gravitation multipliée par la hauteur, soit v = sqrt(2gh) (**) où "sqrt" signifie "racine carrée" ("square root" ou "sqrt" en anglais). La gravitation terrestre étant égale à 9,80665 mètres par seconde carrée, la vitesse en chute libre de notre boule est donc égale à 4,43 mètres par seconde, et l'énergie cinétique (Ec) est égale à 147 joules.
(**) Note informative mais non indispensable pour la bonne compréhension de cette page: l'origine de la formule "v = sqrt(2gh)" s'explique ainsi: l'énergie cinétique (Ec), vue plus haut, intervient aussitôt qu'il y a mouvement de l'objet mais l'objet au repos possède une énergie appelée énergie potentielle (Ep) qui est le produit de la masse multipliée par la gravité, multipliée par la hauteur (distance qui sépare l'objet du sol); cela s'écrit "Ep = mgh" et comme Ep devient Ec aussitôt que l'objet se met en mouvement (chute), on peut dire que "Ep = Ec" ou encore "mgh = mv²/2"; comme la masse n'intervient plus dans la chute libre d'un corps (ce sera expliqué plus tard dans la page) "mgh = mv²/2" devient "gh = v²/2"; si on multiplie chaque terme de cette formule par 2 on obtient "2gh = v²"; et si on porte à la racine carrée chaque terme de cette formule on obtient "sqrt(2gh) = v" ou encore "v = sqrt(2gh)".
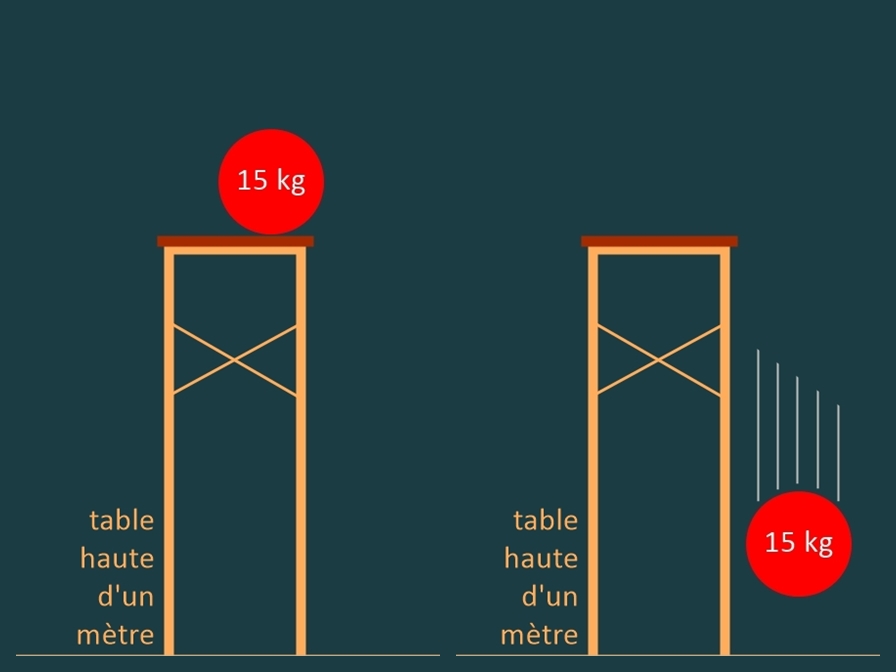
Combien même on ne souhaite pas recevoir sur nos pieds une boule de 15 kilogrammes tombant d'une hauteur de 1 mètre, la partie énergie cinétique est INSIGNIFIANTE comparée à la partie énergie de masse de cette boule (147 joules d'un côté et 15 mille fois 90 milliards de kilojoules de l'autre). Pour autant, ces deux énergies se cumulent.
Une balle de tennis de table, qui pèse 2,7 grammes, ne nous ferait, quant à elle, aucun mal si elle retombait sur nos pieds d'une hauteur de 1 mètre. Son énergie cinétique serait de 0,03 joules. Cependant, son énergie de masse s'élèverait quand même à 243 milliards de kilojoules.
Tant d'énergie de masse que nous ne ressentons pas, que nous ne voyons pas! POURQUOI?
Oui, pourquoi?
Pourquoi, alors que la balle de ping-pong tombe sur nos pieds, ne ressentons-nous que les 3 centièmes de joule de l'énergie cinétique de celle-ci et non pas les 243 milliards de kilojoules de son énergie de masse?
Cette colossale énergie, bien que présente, n'est pas visible car dans les conditions habituelles même une accélération ou une transformation comme une combustion ou une rupture (*) ne pourront pas libérer cette énergie.
Pour voir cette énergie se libérer il faut passer par des forces inhabituelles, qui n'existent qu'au milieu des noyaux des atomes, et qu'on appelle les FORCES NUCLÉAIRES.
(*) Note: nous avons déjà vu précédemment (mais il n'est pas inutile de le rappeler) que la transformation d'une matière par la combustion ne détruit pas de matière car, dans l'exemple d'une bûche, si nous rassemblons les cendres, toutes les petites particules de fumée et la vapeur d'eau produite par le processus de combustion, et que nous pesons le tout, nous constaterons que la masse est exactement égale à la masse de la bûche avant qu'elle brûle. Et si je casse un caillou en deux, je divise la masse en deux ... sans en perdre. Dans ces deux exemples (bûche et caillou) c'est la loi fondamentale de la conservation des masses.

La section suivante (avant-dernière section) concerne cette FORCE NUCLÉAIRE qui peut libérer de l'énergie de masse.
7

7 . L E S F O R C E S N U C L É A I R E S
Rappel: nous venons de voir que l'énergie de masse est gigantesque du seul fait que même une toute petite masse comme celle d'un grain de sable voit son énergie égale au produit de cette masse avec le carré de la vitesse de la lumière. Mais cette énergie de masse est inerte.
Question: peut-on libérer cette énergie de masse de sorte qu'elle ne soit plus de l'énergie inerte? Et qu'elles en seraient les conséquences? Et pour quelles applications?
Réponse: oui, par la fission de l'atome (fission signifie action de fendre, de casser, de diviser). La fission d'un noyau d'uranium ou de plutonium (*) libérera une très grande quantité d'énergie. Ce dégagement est dû à une variation de l'énergie interne (énergie de masse) des noyaux. La fission de l'atome peut avoir des origines tout à fait naturelles comme, par exemple, dans une étoile que nous connaissons bien: le Soleil. La réaction nucléaire et permanente dans le Soleil fournit une énergie colossale qui nous éclaire et nous chauffe. Le Soleil est un objet céleste 109 fois plus grand que la Terre (et distant de 150 millions de kilomètres de celle-ci). La très grande gravité du Soleil a pour conséquence de générer en son centre une température gigantesque (15 à 20 millions de degrés celsius, comparativement celle de la Terre est entre 6 et 6,5 mille degrés Celsius). C'est cette température très élevée du Soleil qui provoque une réaction nucléaire (fission de l'atome) permanente et fait d'elle une étoile (lumière et chaleur).
(*) Note: l'uranium et le plutonium contiennent des atomes fissiles c’est-à-dire des atomes dont le noyau a la capacité de se casser (de se fendre, de se diviser). L'uranium est un métal assez répandu dans le sous-sol de la Terre. Il est contenu dans des minerais (**), qui sont extraits de gisements à ciel ouvert ou en galeries souterraines. Ces gisements se trouvent essentiellement en Australie, aux États-Unis, au Canada, en Afrique du Sud et en Russie. Et un peu en France (peut-être que les gisements ne sont plus en activité): Massif Central, Vendée, Bretagne et Alsace.
(**) Note: les minerais sont des roches contenant des minéraux. Un minéral (singulier de minéraux) est un coprs solide naturel homogène avec une structure atomique bien ordonnée (***) comme, par exemple, le quartz ou la galène ou l'émeraude, etc.
(***) Note: une structure atomique bien ordonnée caractérise tout corps solide homogène composé d’atomes (ou de molécules) dont l’organisation dans l’espace est géométrique (très régulière et très ordonnée).
Conséquences: la fission s’accompagne d’un très grand dégagement d’énergie sous 3 formes:
• explosion (souffle),
• rayonnement thermique (chaleur),
• rayonnement nucléaire (radioactivité).
Applications: bombe atomique et centrale nucléaire. La première application repose sur une volonté de destruction. La deuxième sur un mode de fabrication de l'électricité. Une centrale nucléaire est-elle donc une bombe contenue?
Non! Et voici pourquoi ...

... une bombe atomique a besoin d'une réaction en chaîne: la fission du noyau de l'atome d'uranium libère des neutrons qui vont à leur tour fendre d'autres noyaux d'uranium (dans un espace où ont été concentrés beaucoup de noyaux d'uranium) et ainsi de suite;
... une centrale nucléaire limite considérablement la réaction en chaîne: seulement 3% des noyaux d'uranium concentrés dans un espace sont fissibles (*) et le tout est plongé dans l'eau (piscine) pour limiter les dangers;
la radioactivité reste cependant un danger dans les deux applications.
(*) Note: pour une réaction en chaîne, il faut des noyaux d'uranium fissible et c'est le cas de l'uranium 235 utilisé dans une bombe atomique. Dans une centrale nucléaire seuls 3% d'uranium 235 sont utilisés, le reste étant de l'uranium 238 qui est non fissible. Les 3% d'uranium fissible suffisent à dégager la chaleur nécessaire pour générer de l'électricité.
8

8 . C O N C L U S I O N
Derrière la formule E = mc² il faut lire trois choses:
1) le gigantesque potentiel en énergie qu'il y a dans la matière, même dans un grain de sable;
2) l'énergie peut se transformer en matière et inversement comme dans les centrales nucléaires où de la matière disparaît pour créer de l’énergie;
3) l'énergie "enfermée" dans la matière est restée inerte jusqu'au jour où l'homme a utilisé la découverte d'Albert EINSTEIN en fendant (cassant) le coeur de l'atome pour libérer des forces gigantesques dont les premières applications rappellent le nom de deux villes japonaises: Nagasaki et Hiroshima.
9

9 . D E R N I È R E Q U E S T I O N
J'ai ajouté une section intitulée "dernière question" après la conclusion, tel un épilogue qui serait la conclusion de la conclusion pour poser l'ultime question sans laquelle cette page ne dirait pas tout et certainement pas l'essentiel sur E = mc².
Pour être abordable et compréhensible, la lecture de cette dernière section exige une "préparation du terrain", indispensable, obtenue par la lecture des 8 sections précédentes.
Cette question est la suivante:
Cette question est le titre d'un article de trois pages publié en Allemagne par Albert EINSTEIN en 1905 dans la revue scientifique berlinoise (créée en 1790) "Annalen der Physik" dont le titre original est "Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?" qui se traduit pas "L'inertie d'un corps dépend-elle de l'énergie qu'il contient?".
Il existe une traduction en anglais de cet article intitulé: "Does the inertia of a body depend upon its energy content?".
Albert EINSTEIN avait souhaité publier cet article, sous la forme d'une question, afin de produire la réponse qui démontre que l'inertie d'un corps dépend bien de l'énergie qu'il contient.
QUE DIT OU SOUS-ENTEND CET ARTICLE (3 POINTS)?:
Les 3 points abordés ci-dessous sont: la masse, la vitesse de la lumière et l'inertie.
Afin de mieux appréhender ces 3 points, il est utile de se rappeler:
- que tout corps possède une masse,
- que la masse est la quantité de matière (*) de ce corps,
- que les atomes sont les constituants élémentaires (fondamentaux) de la matière,
- que les atomes sont de l'énergie (dite de masse, voir section 5),
- que, en conséquence de ce qui précède, la masse est du contenu en énergie,
et donc bien se rappeler que la masse est du contenu en énergie, qui est le principal enseignement laissé par Albert EINSTEIN quand il disait que "la masse n'est qu'une mesure de l'énergie d'un corps".
(*) Note: la matière se présente sous la forme de quatre états (les plus communs): l'état solide, l'état liquide, l'état gazeux et l'état plasma. Juste pour information, l'état plasma est un gaz ionisé dans lequel certains électrons sont libres et ne sont plus attachés à un atome ou à une molécule.
Premier point:

♦ La masse est du contenu en énergie. La formule E = mc² peut également s'écrire m = E/c² et ainsi confirme que la masse est bien la mesure totale de l'énergie contenue dans un corps. Illustration avec l'image ci-dessous: la petite bille ne fera pas bouger d'un iota la lourde boule de pétanque mais, au contraire, la lourde boule de pétanque n'aura aucun mal à projeter la bille. Pourquoi? Parce que la boule de pétanque contient beaucoup plus d'énergie que la bille. Cette grande énergie est directement liée à la masse (m = E/c²) et dans la vie quotidienne une boule de pétanque possède davantage de masse qu'une bille en verre. Il en serait exactement de même dans le vide absolu en absence de toute gravitation. L'énergie contenu dans tout corps (sa masse!) n'est en rien liée à la gravitation. La boule de pétanque pourrait être "posée" dans l'espace interstellaire (gravitation quasi-nulle) et être frappée par une bille en mouvement, le constat serait le même que celui observable sur la Terre. Enfin, ne jamais confondre poids et masse: une boule de pétanque aura la même masse sur la Terre comme sur la Lune , mais en tombant sur le pied de la même hauteur elle sera 6 fois plus douloureuse sur Terre que sur la Lune (80 fois moins massive que la Terre) car son poids est lié à la gravitation (la masse, jamais!).
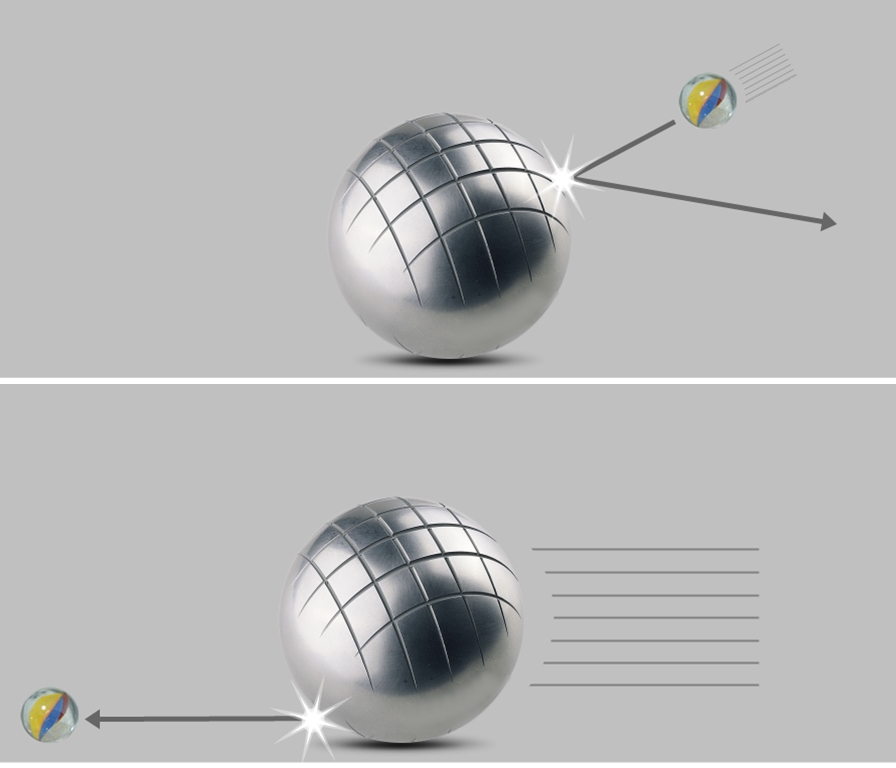
Deuxième point:

♦ La vitesse de la lumière DANS LE VIDE est une constante. Elle est fixe. Elle ne varie pas. Elle est un axiome (*). Le terme c² (rappel: "c" comme célérité ou vitesse de la lumière, portée au carré) est une constante physique. Sa valeur est donc invariable. La présence ou l'absence de gravitation n'ont aucune incidence sur la vitesse de la lumière. Ces points sont fondamentaux car ainsi la masse d'un corps (et donc son énergie) reste constante quand il est isolé. Un corps est dit "isolé" quand il n'échange avec l'extérieur ni matière, ni chaleur et ni travail.
Albert EINSTEIN dit exactement ceci (c'est un postulat): "La vitesse de la lumière est, dans tout référentiel, une constante et est indépendante du mouvement de la source de lumière". Autour de nous, tout est en perpétuel mouvement et peut donc influencer toutes les observations:
a) notre planète tourne sur elle-même,
b) notre planète tourne autour du Soleil,
c) et le tout est en mouvement car notre galaxie (la Voie Lactée) tourne aussi sur elle-même,
aussi avons-nous besoin d'un référentiel. Aussitôt que l'on parle de mouvement, les notions trajectoire et vitesse viennent à l'esprit. Il y a cependant une troisième notion indispensable que l'on appelle "référentiel" c'est-à-dire un ensemble de points fixes nécessaires pour mesurer ce mouvement. Et une même mesure sera différente en fonction du référentiel choisi. Un exemple pour comprendre: un observateur qui regarde depuis sa fenêtre un train qui passe le verra passer à une certaine vitesse. Un autre observateur dans une automobile qui roule parallèlement à la voie ferrée à la même vitesse et dans le même sens que le train ne verra pas ce train passer à la vitesse constatée par l'observateur à sa fenêtre mais verra un train "immobile". Car les deux observateurs ne sont pas dans le même référentiel. Les notions de "mouvement" et d' "immobilité" n'ont de sens que relativement à un référentiel donné (notez que la notion d'immobilité absolue n'existe pas).
Par contre, la vitesse de la lumière est la même dans tous les référentiels. Constat (postulat (*) d'EINSTEIN) par un exemple: sur une route en ligne droite, un piéton voit une voiture qui, de loin, arrive vers lui (elle roule à 80 km/h). Il voit également une autre voiture stationnée sur le bas-côté, chauffeur au volant mais moteur arrêté. Les phares des deux voitures sont éteints et orientés vers le piéton. Au moment précis où la voiture qui roule passe au même niveau que celle stationnée sur le bas-côté, son chauffeur fait un appel de phares (éclair de lumière). De même, au moment précis où la voiture stationnée sur le bas-côté voit passer, à sa hauteur, la voiture qui roule, son chauffeur fait également un appel de phares (éclair de lumière). Les deux appels de phares des deux voitures ont été déclenchés exactement au même moment, à la seconde près, au millième de seconde près. Le piéton devrait voir l'appel de phares de la voiture qui roule avant celui de la voiture stationnée. Il n'en est rien. Le piéton voit les deux appels de phares exactement au même instant. Il en aurait été de même si la voiture qui roule avait fait du 200 km/h. Pourquoi? Parce que si on ajoutait, en toute logique, à la vitesse de la lumière, la vitesse du véhicule, on dépasserait alors la vitesse de la lumière, ce qui est impossible! Note: le postulat, en quoi la vitesse de la lumière ne peut jamais être dépassée, est la base de la Relativité Restreinte, théorie formelle élaborée par Albert EINSTEIN. Les implications de la Relativité Restreinte (1905) et plus tard de la Relativité Générale (1915) sont très nombreuses mais débordent du sujet traité ici. Pour revenir à l'exemple ci-dessus il faut surtout retenir que la vitesse de la lumière est la même dans tous les référentiels.
(*) Note: un axiome est un postulat ou un principe, considéré comme évident en soi, indémontrable, utilisé comme fondement d’un raisonnement ou d’une théorie mathématique. C'est un constat qui ne connait pas d'exceptions (pas de contradictions). Axiome célèbre en géométrie euclidienne (géométrie sur un plan): "Par un point extérieur à une droite, on ne peut mener qu'une et une seule parallèle à cette droite". Par contre, "Dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés" n'est pas un axiome mais un théorème (dont l'auteur est Pythagore) car cette affirmation peut être démontrée (**).
(**) Note: la démonstration du théorème de Pythagore est simple (rapide et "amusante") et consultable en cliquant ici → voir (•_•) ← même si cela n'a pas de lien direct avec le contenu de cette page.
Troisième point:

♦ Tout d'abord il faut définir ce qu'on appelle l'inertie, mot qui n'a pas encore été utilisé dans cette page (jusqu'ici).
Première définition proposée: l'inertie est la propriété qu'ont les corps de ne pouvoir d'eux-mêmes changer l'état de repos ou de mouvement où ils se trouvent.
Deuxième définition proposée: l'inertie est la résistance passive qu’opposent les corps du fait de leur masse au changement de l’état de repos ou de mouvement dans lequel ils se trouvent.
Ces deux définitions sont parfaitement correctes mais un peu absconses et un exemple concret devrait apporter toute la lumière:
On sait que la vitesse de la chute d'un corps ne dépend pas de sa masse. Dans le vide, une boule de pétanque et une plume d'oiseau tomberont à la même vitesse et toucheront donc le sol en même temps. Cette expérience est difficile à vérifier dans son jardin car l'air ambiant sera un élément de résistance pour la plume (qui va voltiger). Mais au lieu d'une plume d'oiseau, on peut faire l'expérience concluante avec une balle de tennis par exemple, qui offrira une résistance négligeable à l'air. Une boule de pétanque pèse environ 700 grammes alors qu'une balle de tennis pèse un peu moins de 60 grammes (elle est donc 11 fois plus légère).
Question: pourquoi deux objets de masse différente vont-ils tomber à la même vitesse, en même temps (bien parallèlement) et en touchant le sol en même temps?
Cette question a un sens car la boule de pétanque est bien plus lourde sur la balance qui montre qu'elle subit une force gravitationnelle de 700 grammes alors que sur la même balance le poids de la balle de tennis subit une force gravitationnelle de seulement 60 grammes.
Réponse:
Surprenant? Certes!
Contre-intuitif? Oui, car cela va à l’encontre des apparences.
Et pourtant c'est la base de la théorie d'Albert EINSTEIN appelée Relativité Générale (1915). Après plus d'un siècle, toutes les observations et découvertes ont confirmé cette thèse. C'est un constat. La Terre, de tous les points de la Terre, est en PERMANENTE ACCÉLÉRATION qui est de 10 mètres par seconde (environ) et qui porte le nom de "g" comme gravité.
Comment une sphère (la Terre!) peut-elle être en accélération "rayonnante" sans ... "exploser"? Comment un objet (un corps) peut-il être en constante accélération sans atteindre, avec le temps, des vitesses vertigineuses? Il est très difficile de conceptualiser un tel constat car l'homme a besoin de modéliser des comportements pour les comprendre et les expliquer.
Un siècle plus tard (en 2017) le satellite français Microscope (c'est son nom) est allé vérifier que dans le vide 2 objets de masse différente dans le même champ gravitationnel "tombent" en même temps (donc parallèlement et à la même vitesse). La différence d'impact (temps écoulé entre le moment d'impact du premier objet et le moment d'impact du deuxième objet) est de 1 pour 0,5 multiplié par 10 puissance 14.
Pour mieux comprendre ce qui précède (en 5 images):





Il n'y a aucune expérience physique qui permettrait à la personne dans la fusée en accélération de savoir si elle est sur Terre ressentant alors les effets de la gravitation terrestre ou si elle est dans l'espace ressentant alors les effets de l'accélération.
L'effet d’un mouvement accéléré est localement impossible à distinguer de celui produit par une force de gravitation.
Albert EINSTEIN a appelé ce postulat ...
LE PRINCIPE D'ÉQUIVALENCE
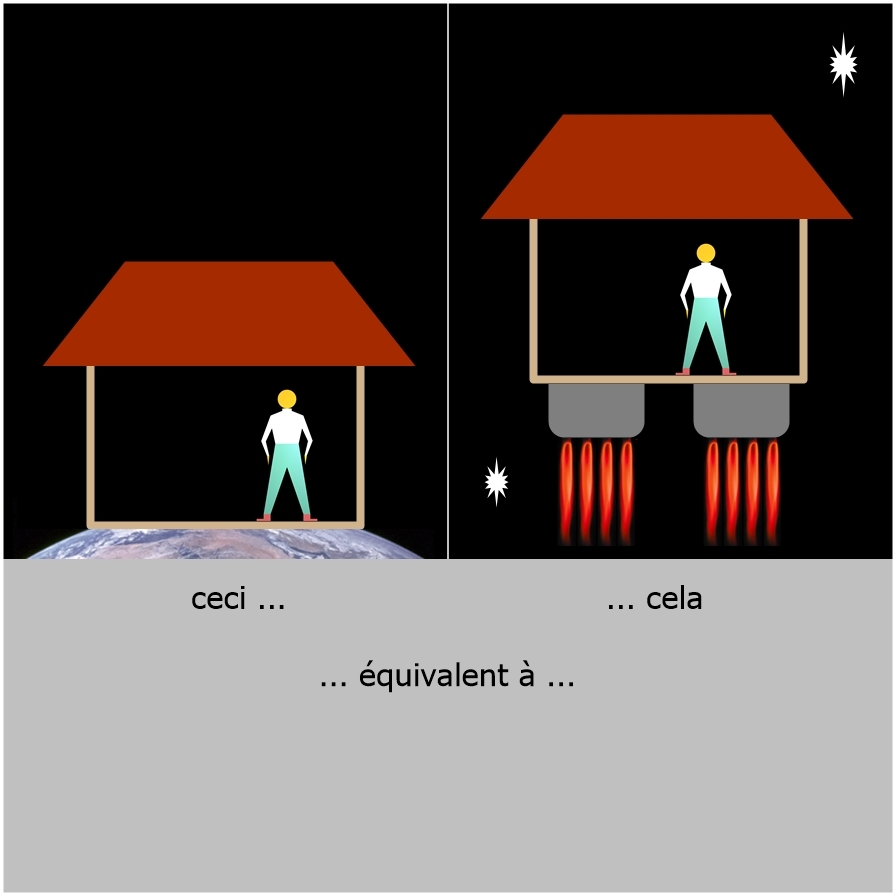
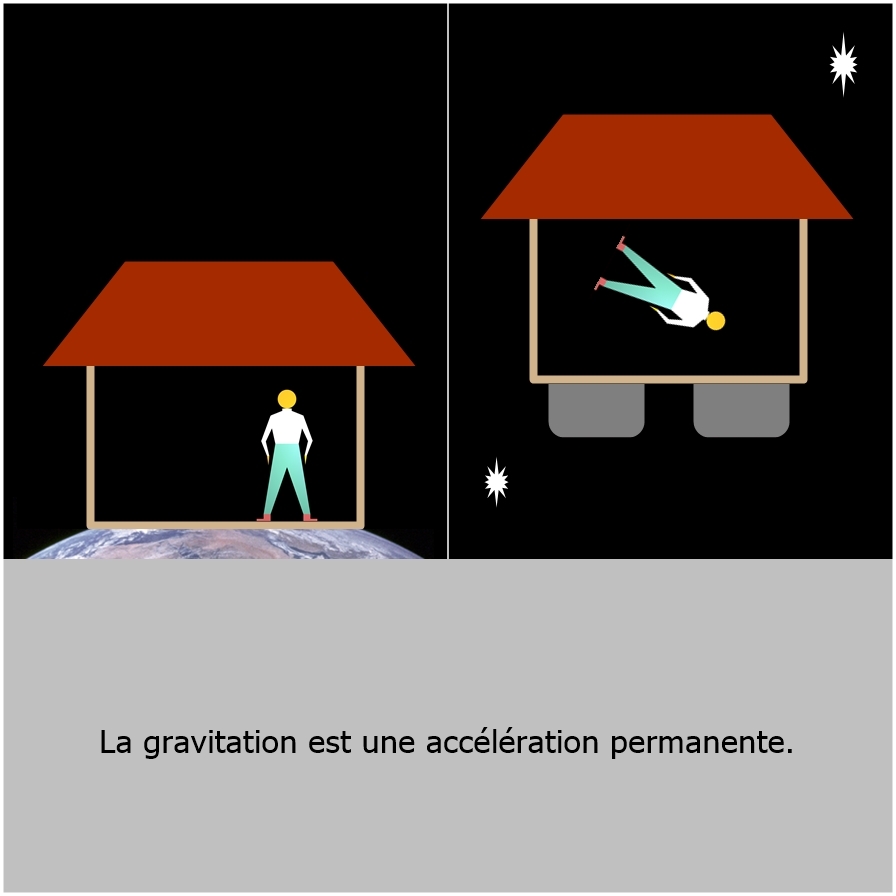

Extrait (mot pour mot) de propos d'un exposé en vidéo sur Internet du physicien et philosophe français Étienne KLEIN ("Si la relativité générale m’était contée" consultable sur YouTube):
Au mois de mai 1907, à l'époque EINSTEIN est ingénieur à l'Office Général de la Propriété Intellectuelle, et un après-midi, après le déjeuner, il rêvasse - il le raconte lui-même - et lors de cette rêverie semi-éveillée il a, dit-il, l'idée la plus heureuse de sa vie. Alors, qu'elle est cette idée? Il le dit: "J'ai compris qu'une personne en chute libre ne sent pas son propre poids. Ça a provoqué en moi une très forte émotion, dit-il, qui m'a conduit quelques années plus tard à une nouvelle théorie de la gravitation", fin de citation. Que veut-il dire par là? Eh bien, si vous tombez en chute libre, les choses qui tombent avec vous, par exemple votre parapluie ou votre chapeau, tombent comme vous puisque nous savons que tous les corps tombent à la même vitesse dans le vide. Donc, le poids qui est la cause de votre chute fait que pendant la chute les objets qui tombent avec vous tombent comme vous, c'est-à-dire que par rapport à vous ils ne tombent pas. Quand vous tombez, les objets qui tombent avec vous, vous semblent être en apesanteur et donc l'effet de votre poids, qui est la chute, semble annuler la cause de votre chute qui est le poids. Et donc ce qu'il comprend c'est que finalement une accélération, celle que provoque la chute, semble annuler sa cause qui est la gravitation. Et cela l'amène à formuler, tout de suite après, ce qu'il appelle LE PRINCIPE d'ÉQUIVALENCE entre la gravité et l'accélération. Ça veut dire quoi? Ca veut dire que si vous êtes dans une capsule, hermétique, vous ne savez pas ce qu'il y a à l'extérieur, vous ne pouvez pas faire la différence selon que l'on met la capsule sur la Terre dans un champ de gravité cette capsule étant immobile, c'est-à-dire qu'elle est dans un champ de pesanteur - vous pouvez lancer des balles et observer que leurs trajectoires sont celles que l'on observe habituellement, une trajectoire parabolique par exemple - et puis si au contraire la capsule est dans le vide absolu loin de toute masse donc en dehors de tout champ de gravitation mais accélérée par je ne sais quel Titan qui tirerait sur la capsule pour lui donner une accélération égale à l'accélération de la pesanteur, cette capsule accélérée, si vous êtes dedans, vous allez lancer des balles sur le sol et vous allez voir les mêmes lois physiques que celles qu'il y aurait si vous étiez sur Terre. Donc, pour EINSTEIN les deux situations sont PARFAITEMENT ÉQUIVALENTES et la physique doit se faire l'écho de cette équivalence.
Et l'inertie dans tout cela?
Il suffit d'un bac à sable comme dans l'image ci-dessous, pour voir l'inertie (constat de visu)!
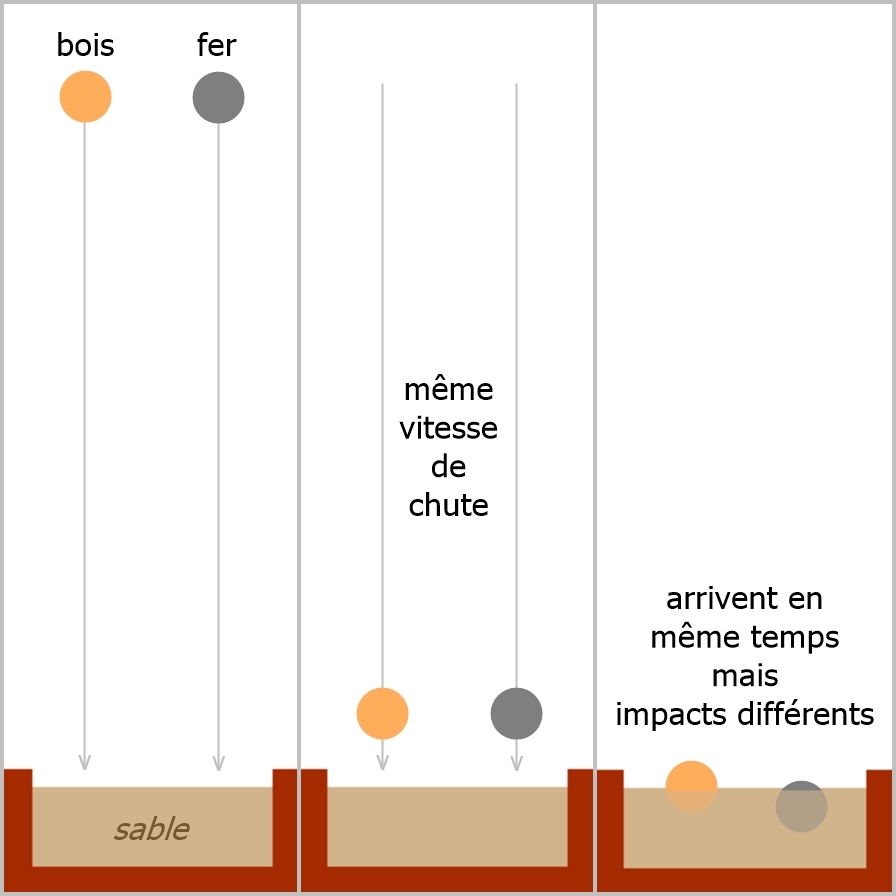
Comme déjà abordé dans la section 4 (énergie cinétique) l'impact sur le sol d'un objet sera fonction de sa masse. Ainsi, 2 boules de même volume (voir image ci-dessus) mais de masse différente, lâchées en même temps de la même hauteur et donc touchant le sol à la même vitesse, ne s'enfonceront pas dans le sable à la même profondeur.
La définition de l'inertie (déjà mentionnée un peu plus haut dans cette section) était: l'inertie est la résistance passive qu’opposent les corps du fait de leur masse au changement de l’état de repos ou de mouvement dans lequel ils se trouvent. Ainsi, la résistance qui s'opposera au mouvement des 2 corps (boule en bois et boule en fer de l'exemple ci-dessus) quand ils rencontreront le sol (donc le bac à sable) se traduira par une force d'inertie visible par la différence de pénétration dans le sable due à la différence de masse des 2 objets. Plus l'objet à une masse importante, plus il aura d'inertie et plus il faudra de force pour l'arrêter.
On peut alors écrire:
Il sera plus difficile pour Popeye de déplacer un objet lourd qui est immobile tout comme il lui sera plus difficile d'arrêter (image ci-dessus) un objet lourd qui est en mouvement.
Et également constater que l'inertie est directement liée à la masse de l’objet: plus cette dernière est élevée, et plus l’inertie est grande De plus, comme la masse est la mesure de l'énergie d'un corps, le pas est vite franchi pour associer directement inertie et énergie: plus l'énergie est élevée, et plus l'inertie est grande.
Ainsi, la question d'Albert EINSTEIN,
• l'inertie d'un corps dépend-elle de l'énergie qu'il contient?
est bien l'affirmation
• l'inertie d'un corps dépend de l'énergie qu'il contient.

