des
cubes en bois
pour des
carrés en maths
cubes en bois
pour des
carrés en maths
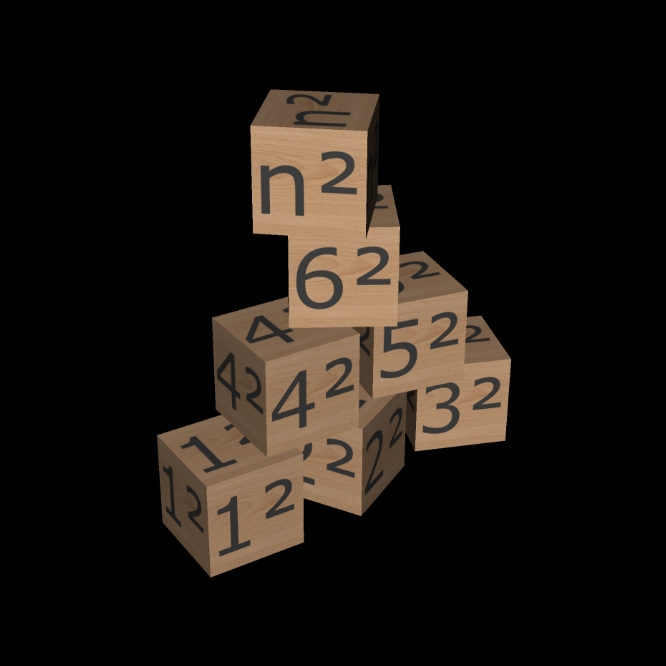

|

|

|
SOMME DES CARRÉS
D'UNE SUITE DES NOMBRES ENTIERS DE 1 À N
Explication d'une formule
La formule pour calculer la somme des carrés d'une suite des nombres entiers de 1 à n est la suivante:
• (voir image ci-dessous)
• (voir image ci-dessous)
--=O=--
Une petite démonstration avec de simples cubes permet très aisément de comprendre comment la formule a été élaborée (ci-après, en plusieurs étapes).
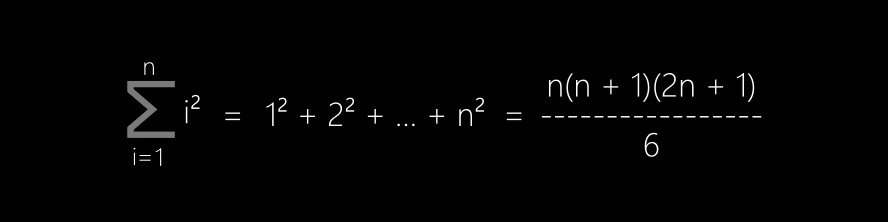
01
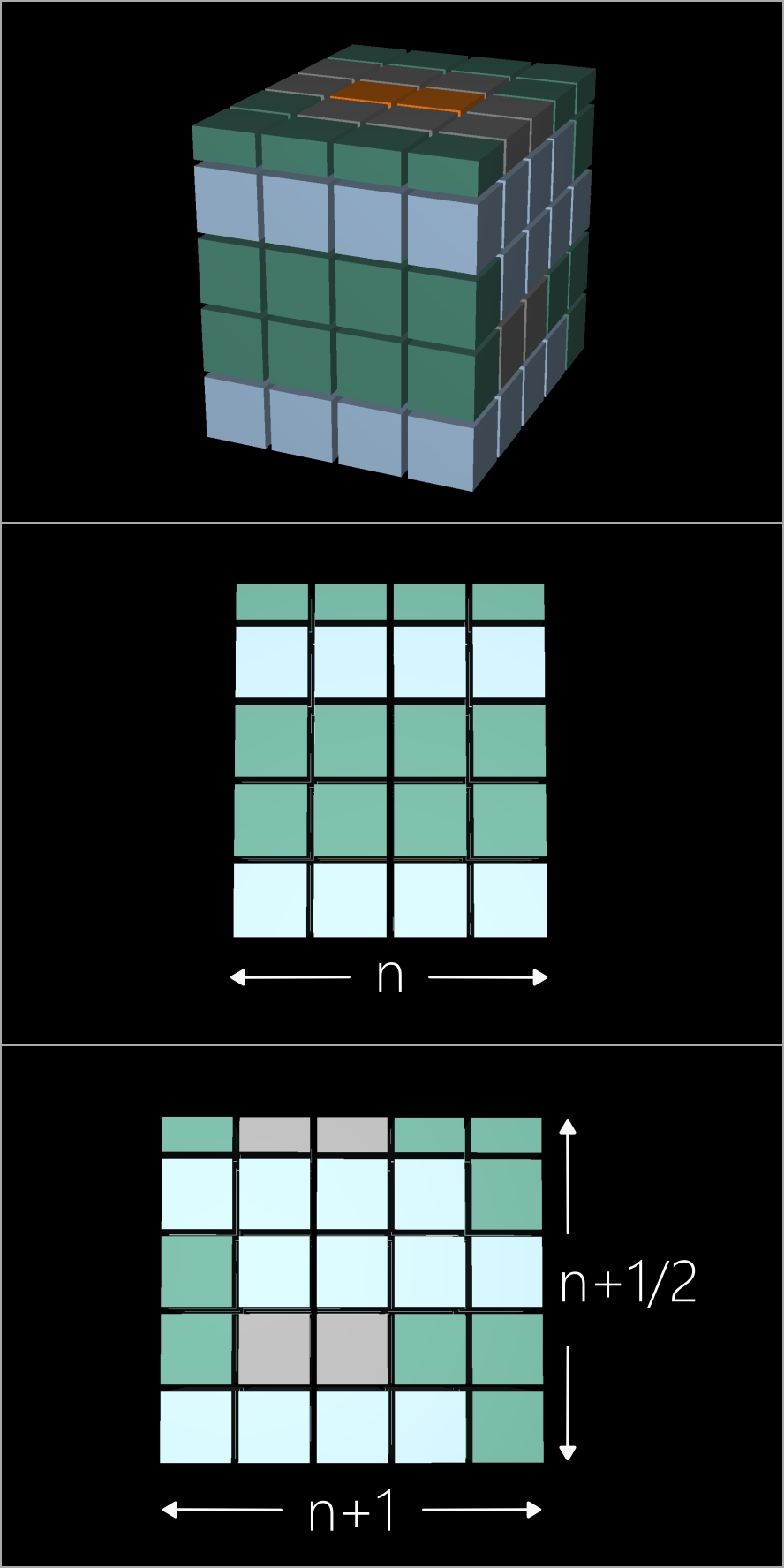
La construction ci-dessous est réalisée avec un cube (orange) monté sur 4 cubes (brun) montés sur 9 cubes (vert) montés sur 16 cubes (bleu).
Sachant que:
• le cube (orange) = 1²
• les 4 cubes (brun) = 2²
• les 9 cubes (vert) = 3²
• les 16 cubes (bleu) = 4²
Ces cubes matérialisent:
• la somme des carrés de 1 à n avec, pour l'exemple, n = 4
Sachant que:
• le cube (orange) = 1²
• les 4 cubes (brun) = 2²
• les 9 cubes (vert) = 3²
• les 16 cubes (bleu) = 4²
Ces cubes matérialisent:
• la somme des carrés de 1 à n avec, pour l'exemple, n = 4

02
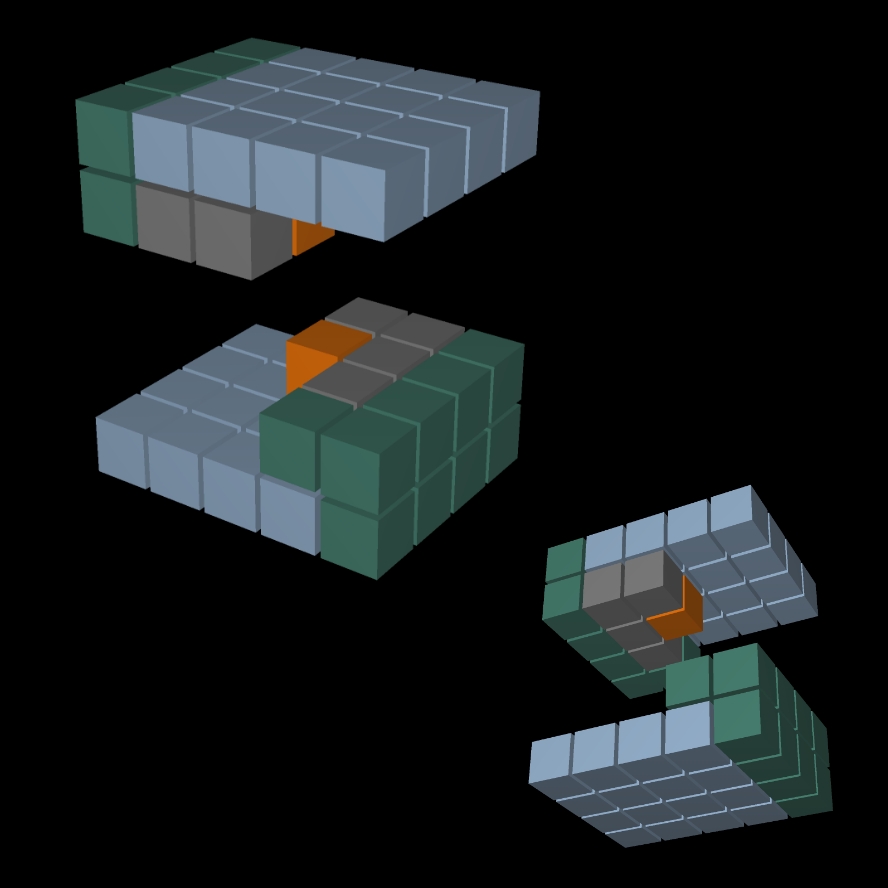
Les cubes sont regroupés sur une base de n sur n+1 cubes (donc 4 sur 5).

03
Le jeu constitué de 30 cubes (1²+2²+3²+4²=30) est dupliqué.
04
On obtient ainsi un bloc de 2 fois 30 cubes.

05
Un troisième, et dernier, jeu de 30 cubes est constitué ...
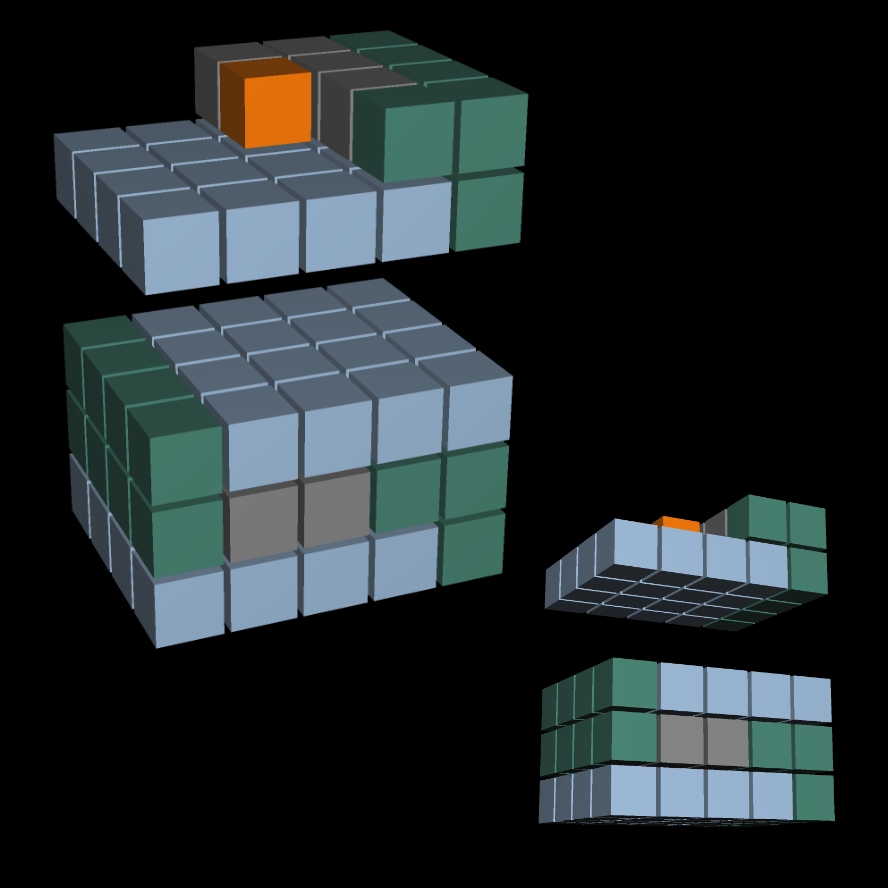
06
... pour former un bloc de 90 cubes.
Ainsi, ce bloc comprend donc:
• 3 fois la suite 1²+2²+3²+4²
Ainsi, ce bloc comprend donc:
• 3 fois la suite 1²+2²+3²+4²

07
On peut procéder à un nivellement des 10 cubes du haut car ils occupent la moitié de la surface (20 cubes).
Ainsi, ces 10 cubes deviennent 20 demi-cubes.
Ainsi, ces 10 cubes deviennent 20 demi-cubes.

08
En conséquence, les dimensions du bloc final sont:
• bloc final = 4 sur 5 sur 4+(1/2)
Comme 4 = n, on peut donc écrire:
• bloc final = n * n+1 * n+(1/2)
• bloc final = 4 sur 5 sur 4+(1/2)
Comme 4 = n, on peut donc écrire:
• bloc final = n * n+1 * n+(1/2)
09
C O N C L U S I O N
Le bloc final est constitué de 3 fois la suite 1²+2²+3²+n²,
et comme ce bloc a pour dimensions n, n+1 et n+(1/2),
en conséquence, on peut écrire:
• 3*(1²+2²+3²+n²) = n*(n+1)*(n+(1/2))
et comme n+(1/2) = (2n/2)+(1/2) = (2n+1)/2
alors:
n*(n+1)*(2n+1)
• 3*(1²+2²+3²+n²) = ----------------
2
ou encore (en divisant les 2 termes par 3):
n*(n+1)*(2n+1)
• 1²+2²+3²+n² = ----------------
6
et comme ce bloc a pour dimensions n, n+1 et n+(1/2),
en conséquence, on peut écrire:
• 3*(1²+2²+3²+n²) = n*(n+1)*(n+(1/2))
et comme n+(1/2) = (2n/2)+(1/2) = (2n+1)/2
alors:
n*(n+1)*(2n+1)
• 3*(1²+2²+3²+n²) = ----------------
2
ou encore (en divisant les 2 termes par 3):
n*(n+1)*(2n+1)
• 1²+2²+3²+n² = ----------------
6
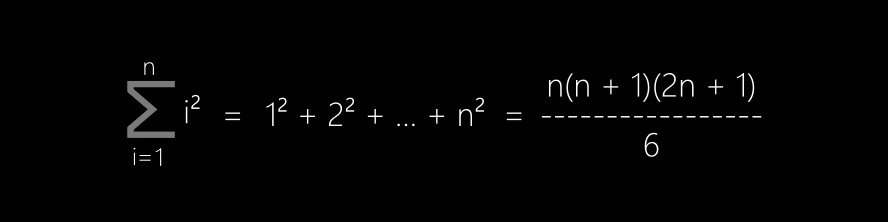
10
Note: la démonstration avec des cubes vaut, bien entendu, pour n'importe quel cas:
• par exemple, 3 fois 140 cubes auraient été nécessaires pour une démonstration avec la suite 1²+2²+3²+4²+5²+6²+7²=140
• le bloc final aurait été constitué de 420 cubes (3*140) sur une base de 7*8 (56 cubes) et une hauteur de 7,5 cubes.
• par exemple, 3 fois 140 cubes auraient été nécessaires pour une démonstration avec la suite 1²+2²+3²+4²+5²+6²+7²=140
• le bloc final aurait été constitué de 420 cubes (3*140) sur une base de 7*8 (56 cubes) et une hauteur de 7,5 cubes.

11

|

|

|
