six
pyramides
dans un
parallélépipède
pyramides
dans un
parallélépipède


|

|

|
VOLUME
D'UNE PYRAMIDE
D'UNE PYRAMIDE
Explication d'une formule
Dans les images qui suivent, la pyramide considérée est une pyramide régulière car ses faces latérales
sont identiques et formées chacune d'un triangle isocèle (ou équilatéral).
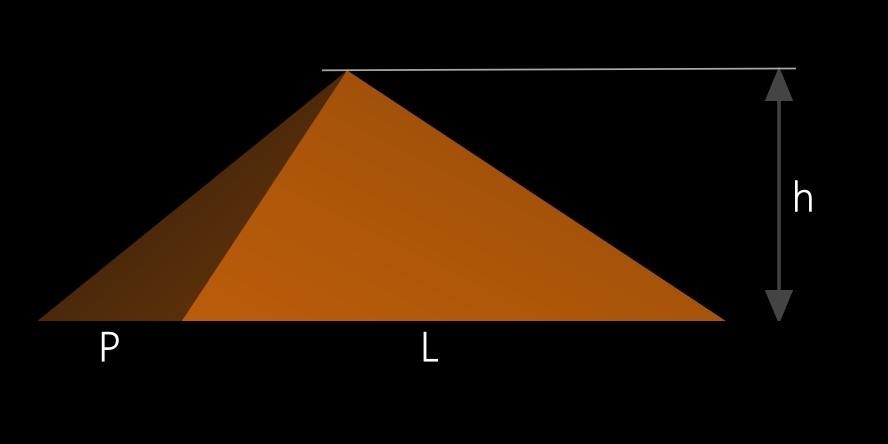
La pyramide considérée ici est une pyramide à base rectangulaire (ou carrée).
La pyramide considérée ici est une pyramide à base rectangulaire (ou carrée).

01
Soit:
• L = longueur de la pyramide
• P = profondeur de la pyramide
• h = hauteur de la pyramide
la formule pour calculer le volume est:

Les images ci-après illustrent une élaboration de cette formule.
• L = longueur de la pyramide
• P = profondeur de la pyramide
• h = hauteur de la pyramide
la formule pour calculer le volume est:

Les images ci-après illustrent une élaboration de cette formule.
02
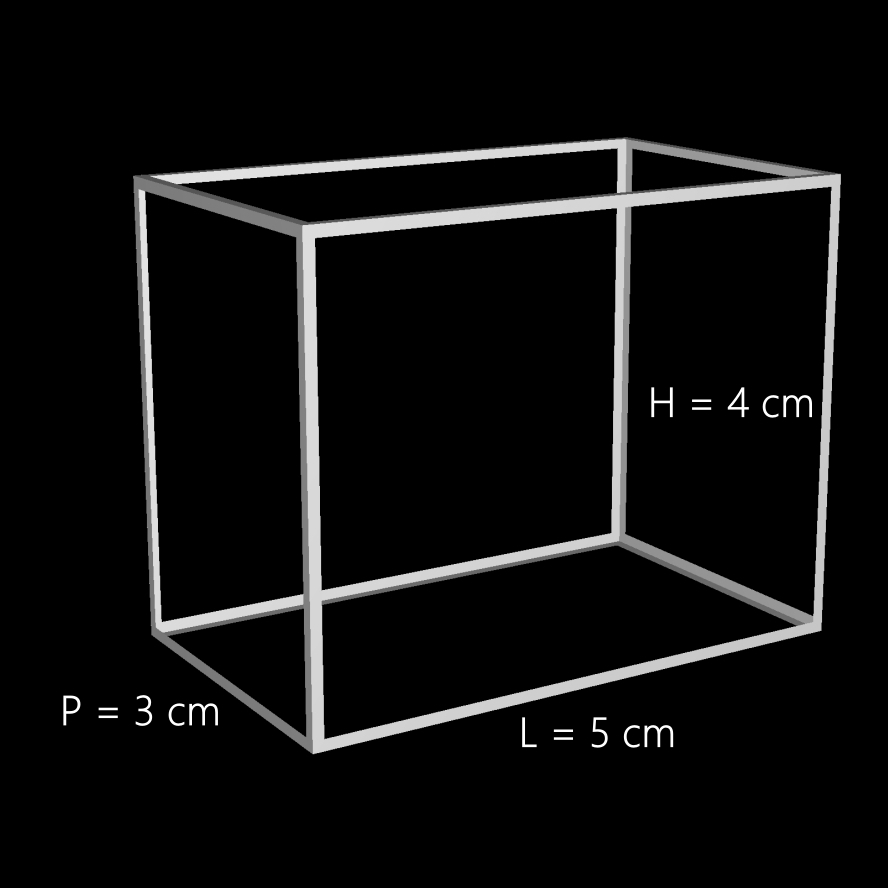
Soit un parallélépipède rectangle (appelé aussi prisme droit) de 5 cm de longueur, 4 cm de hauteur et 3 cm de profondeur ...

03
04
Soit les diagonales de ce parallélépipède: elles sont au nombre de 4 reliant 2 à 2 (de manière opposée) les 8 sommets que compte la figure ...

05
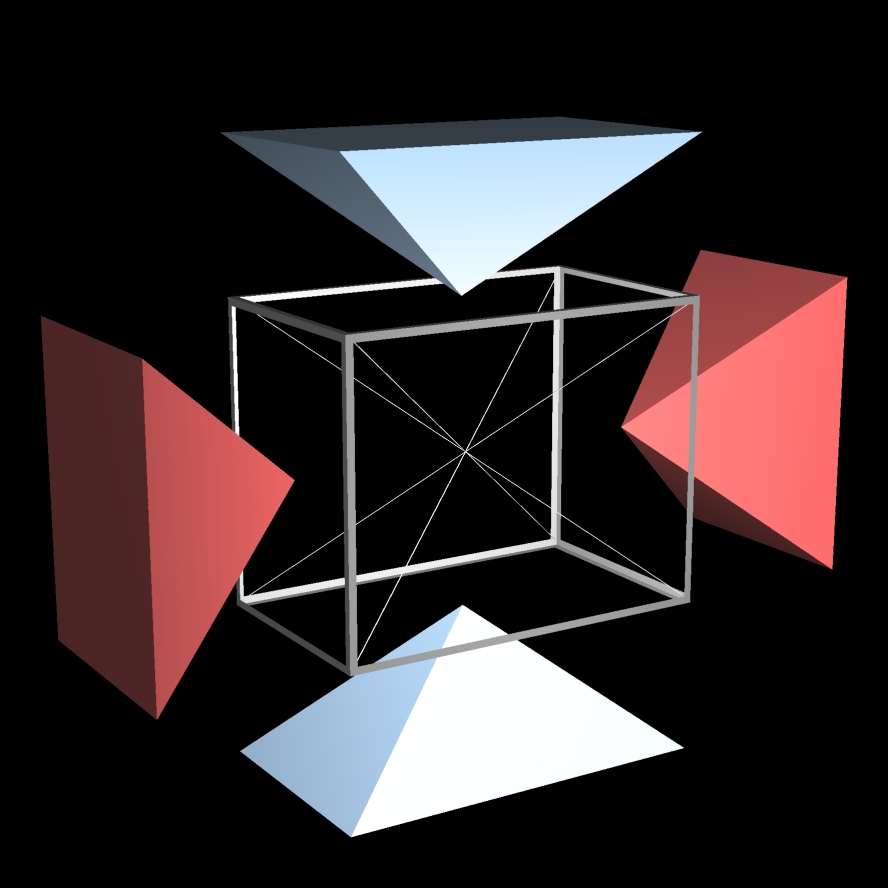
Les diagonales "découpent" le parallélépipède en 6 pyramides (une par face):
• 2 pyramides pour les faces situées à gauche et à droite;
• 2 pyramides pour les faces du dessous et du dessus;
...
• 2 pyramides pour les faces situées à gauche et à droite;
• 2 pyramides pour les faces du dessous et du dessus;
...
06
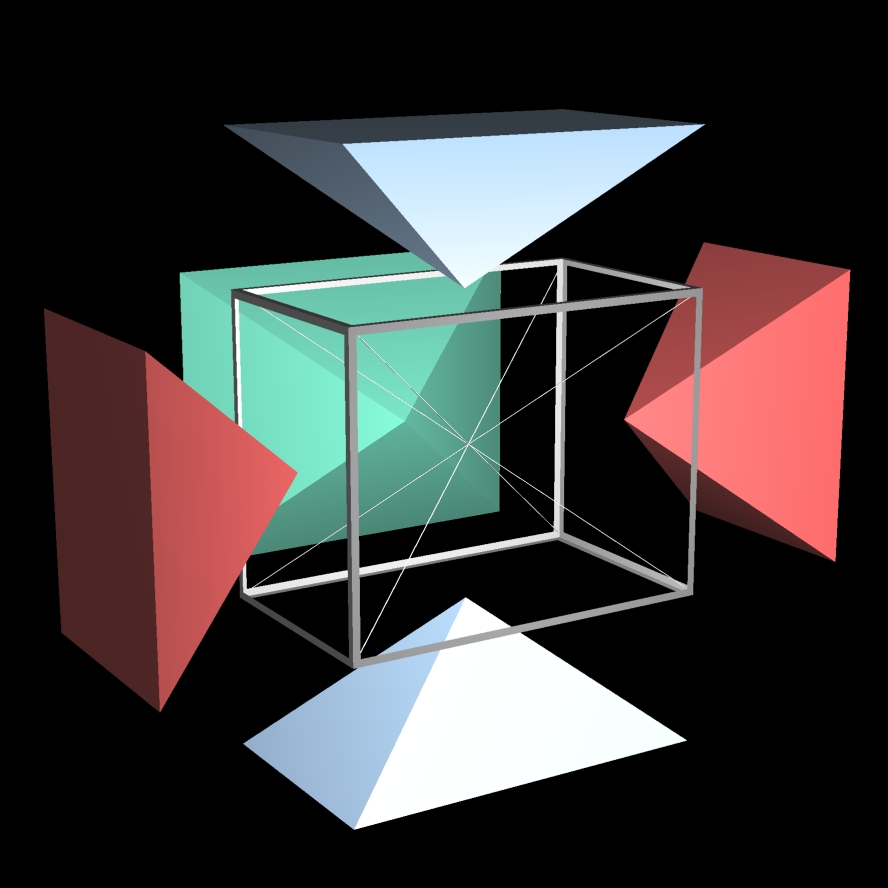
• 2 pyramides pour les faces avant et arrière;
Note: la pyramide de la face avant n'est pas représentée, ici sur l'image, pour des raisons de présentation.
Note: la pyramide de la face avant n'est pas représentée, ici sur l'image, pour des raisons de présentation.
07
Les somments des pyramides convergent vers le milieu du parallélépipède (point d'intersection des diagonales) ...

08
... sans omettre la pyramide de la face avant ...

09
... afin de "reconstituer" le parallélépipède.
• 5 cm * 4 cm * 3 cm = 60 cm³
--=O=--
Le volume du parallélépipède est:
• 5 cm * 4 cm * 3 cm = 60 cm³

10
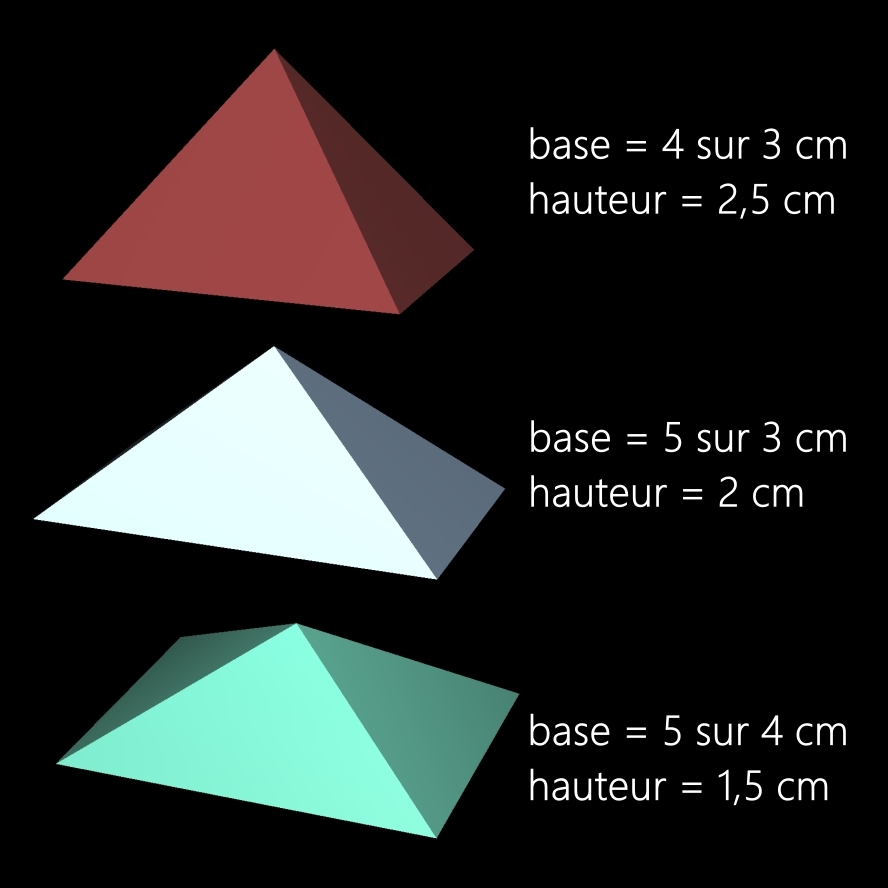
Volume de la pyramide de la face gauche (ou droite):
• (4 cm * 3 cm * 2,5 cm) / 3 = 10 cm³
Volume de la pyramide de la face du dessus (ou du dessous):
• (5 cm * 3 cm * 2 cm) / 3 = 10 cm³
Volume de la pyramide de la face avant (ou arrière):
• (5 cm * 4 cm * 1,5 cm) / 3 = 10 cm³
• (2 * 10 cm³) + (2 * 10 cm³) + (2 * 10 cm³) = 60 cm³
• résultat équivalent au volume du parallélépipède (60 cm³)
• (4 cm * 3 cm * 2,5 cm) / 3 = 10 cm³
Volume de la pyramide de la face du dessus (ou du dessous):
• (5 cm * 3 cm * 2 cm) / 3 = 10 cm³
Volume de la pyramide de la face avant (ou arrière):
• (5 cm * 4 cm * 1,5 cm) / 3 = 10 cm³
--=O=--
Volume total de l'ensemble des 6 pyramides:
• (2 * 10 cm³) + (2 * 10 cm³) + (2 * 10 cm³) = 60 cm³
• résultat équivalent au volume du parallélépipède (60 cm³)
11
C O N C L U S I O N
Les 6 pyramides ont le même volume et le total des 6 volumes est équivalent à celui du parallélépipède rectangle.
On peut donc écrire:
• volume d'1 pyramide = (volume du parallélépipède)/6
• volume d'1 pyramide = (L*P*H)/6
• soit h = la hauteur de la pyramide
• soit H = la hauteur du parallélépipède
• alors h = H/2 ou encore H = 2h
Ainsi, le calcul du volume de la pyramide:
• volume = (L*P*H)/6 devient (L*P*2h)/6 ou encore (L*P*h)/3

On peut donc écrire:
• volume d'1 pyramide = (volume du parallélépipède)/6
• volume d'1 pyramide = (L*P*H)/6
--=O=--
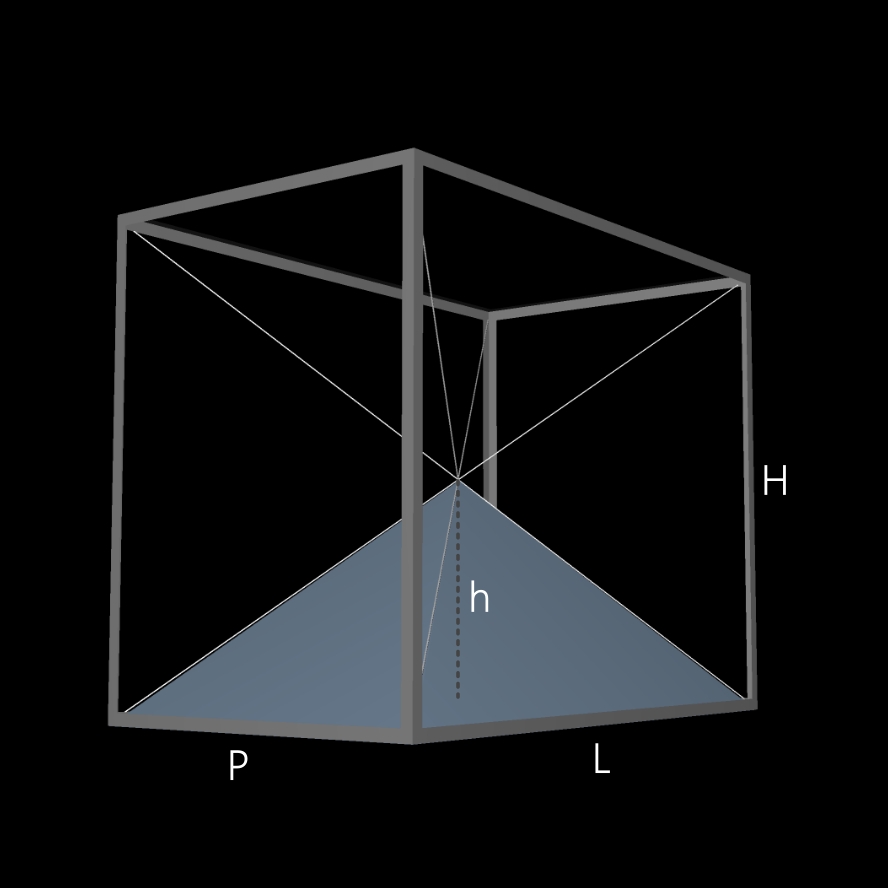
En prenant exemple sur la pyramide située en bas du parallélépipède (voir image ci-dessous), on fait le constat suivant:
• soit h = la hauteur de la pyramide
• soit H = la hauteur du parallélépipède
• alors h = H/2 ou encore H = 2h
Ainsi, le calcul du volume de la pyramide:
• volume = (L*P*H)/6 devient (L*P*2h)/6 ou encore (L*P*h)/3

--=O=--
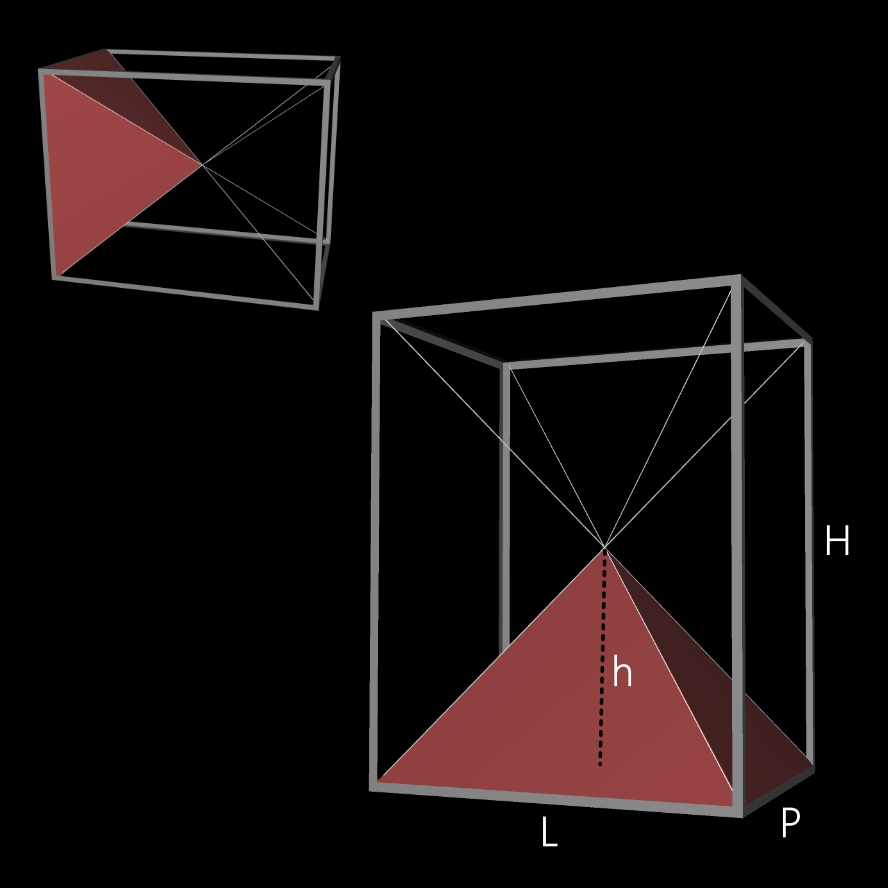
Raisonnement qui s'applique, bien entendu, à TOUTES les pyramides régulières à base rectangulaire ou carrée (voir image ci-dessous-dessous).
--=O=--
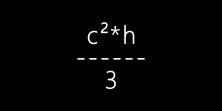
Dans le cas des pyramides régulières à base carrée, la formule est (avec c = côté de la base):

12
13

|

|

|
