l'aire
d'un polygone
pour
l'aire
d'un disque
d'un polygone
pour
l'aire
d'un disque

|

|

|
POLYGONE
Polygone régulier convexe:
Pour calculer la surface (ou aire) d'un disque on utilise la formule Pi*r² (où r est le rayon).
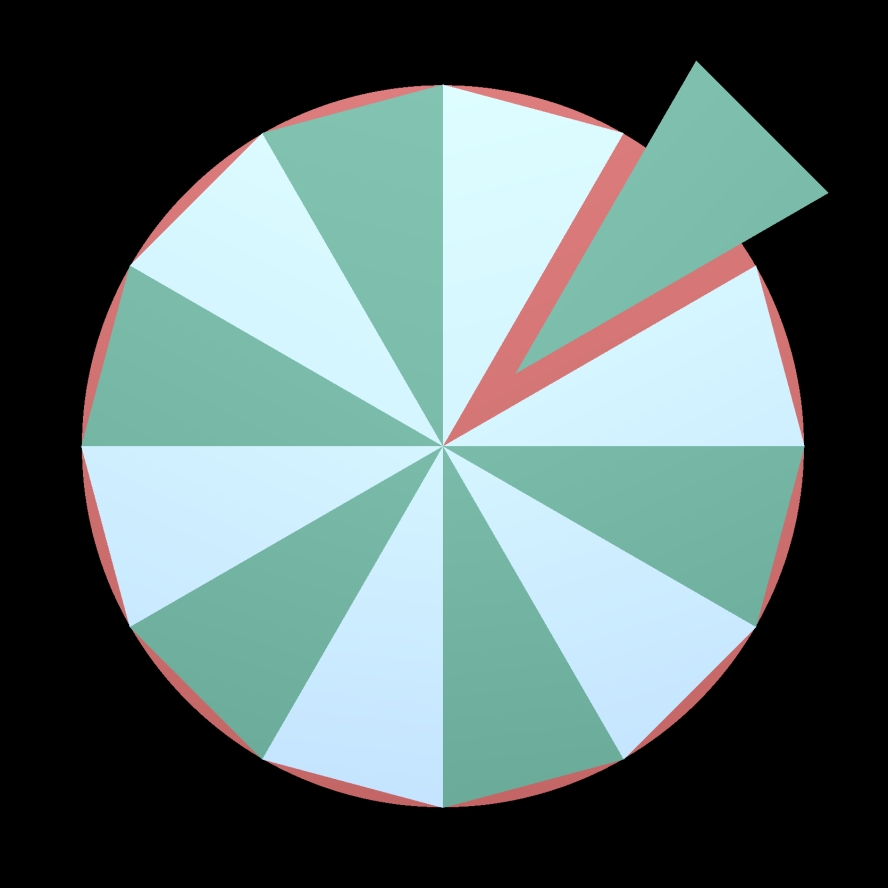
A titre d'exercice, on pourrait calculer la surface de ce disque en calculant la surface d'un polygone régulier (et convexe) circonscrit.
Un polygone régulier est soit convexe, soit étoilé. Dans cette page, seul le polygone convexe est concerné.
A titre d'exercice, on pourrait calculer la surface de ce disque en calculant la surface d'un polygone régulier (et convexe) circonscrit.
--=O=--
Un polygone régulier est un polygone à la fois équilatéral (tous ses côtés ont la même longueur) et équiangle (tous ses angles ont la même mesure).
Un polygone régulier est soit convexe, soit étoilé. Dans cette page, seul le polygone convexe est concerné.

Polygone circonscrit:
Chacun des sommets du polygone passe sur la circonférence du disque. Le polygone est circonscrit (donc contenu à l'intérieur du disque).

Côté, apothème et rayon:
Le polygone est constitué de côtés de même longueur. Chaque côté est également la base d'un triangle isocèle (section du polygone).
L'apothème désigne les segments tracés perpendiculairement des côtés du polygone au centre du polygone.
L'apothème est également la hauteur du triangle isocèle.
L'apothème désigne les segments tracés perpendiculairement des côtés du polygone au centre du polygone.
L'apothème est également la hauteur du triangle isocèle.
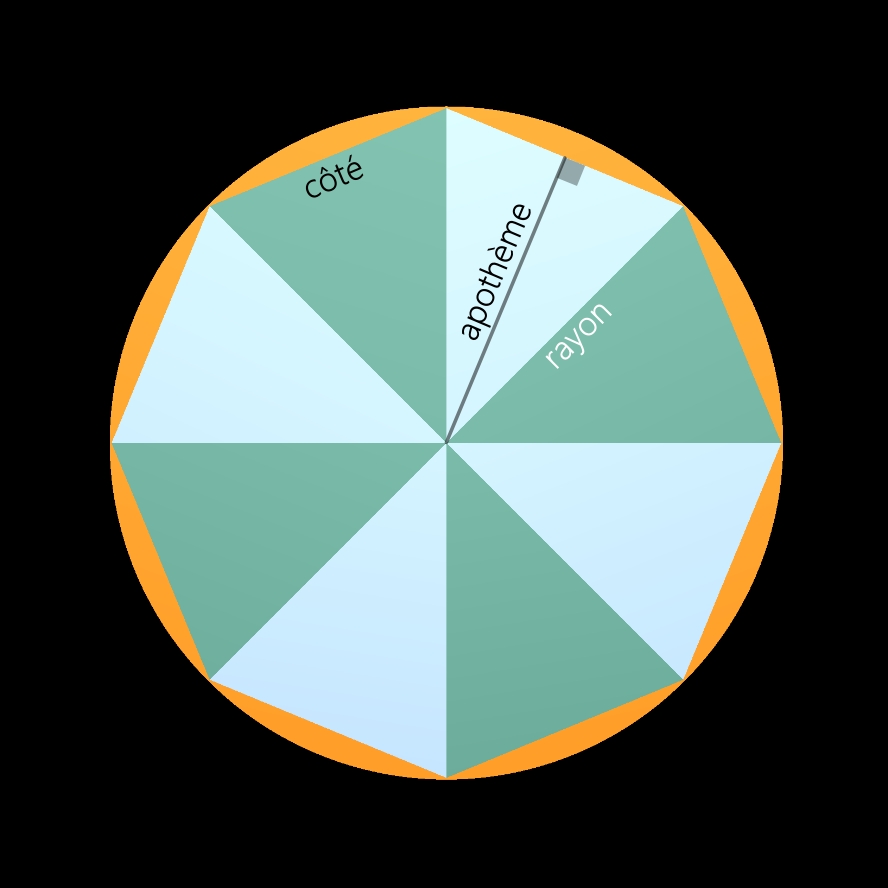
L'apotème presqu'égal au rayon:
Plus les côtés seront petits et plus l'apothème viendra égaliser le rayon.
La surface de l'ensemble des triangles isocèles (et donc du polygone) couvrira la surface totale du disque.
La surface de l'ensemble des triangles isocèles (et donc du polygone) couvrira la surface totale du disque.


|

|

|
AIRE DU POLYGONE
=
AIRE DU DISQUE
=
AIRE DU DISQUE
Calcul infinitésimal:
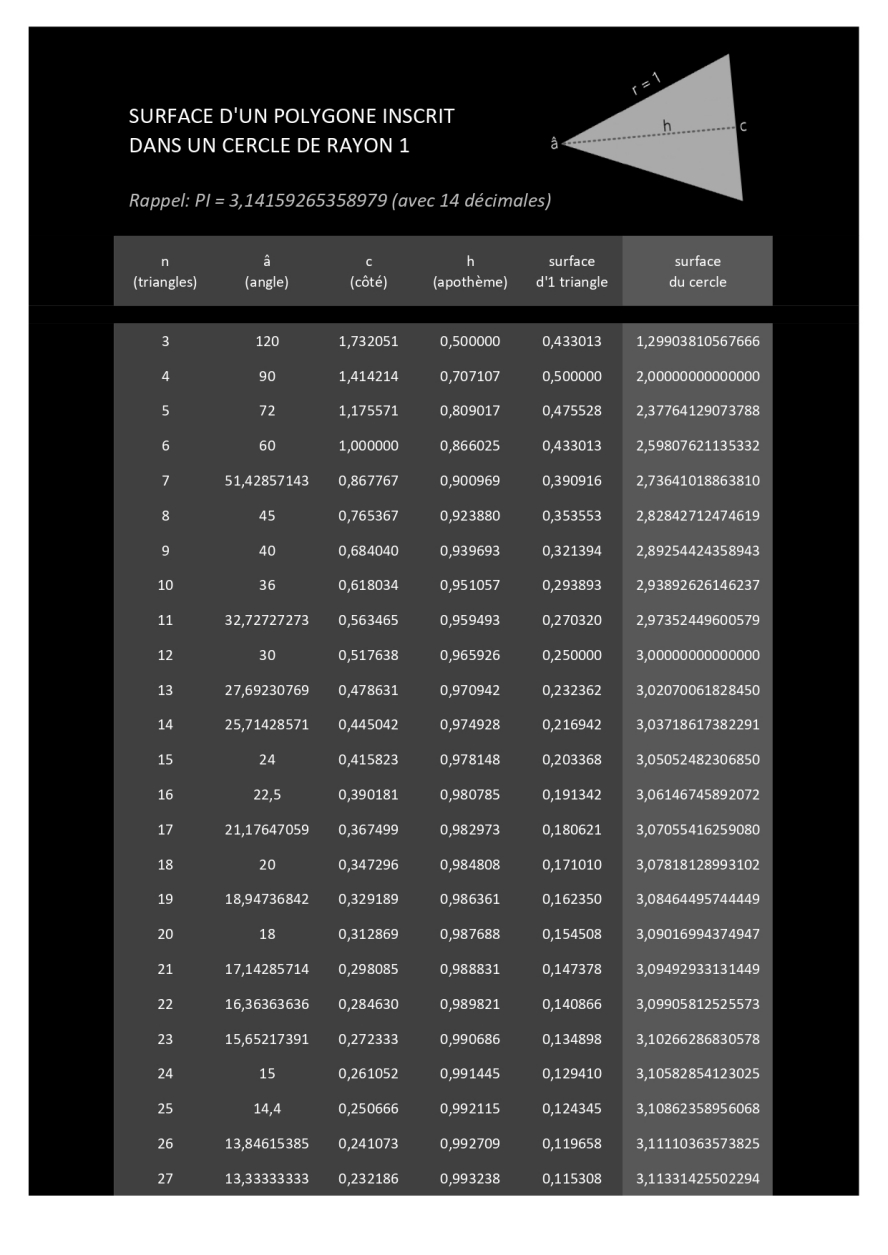
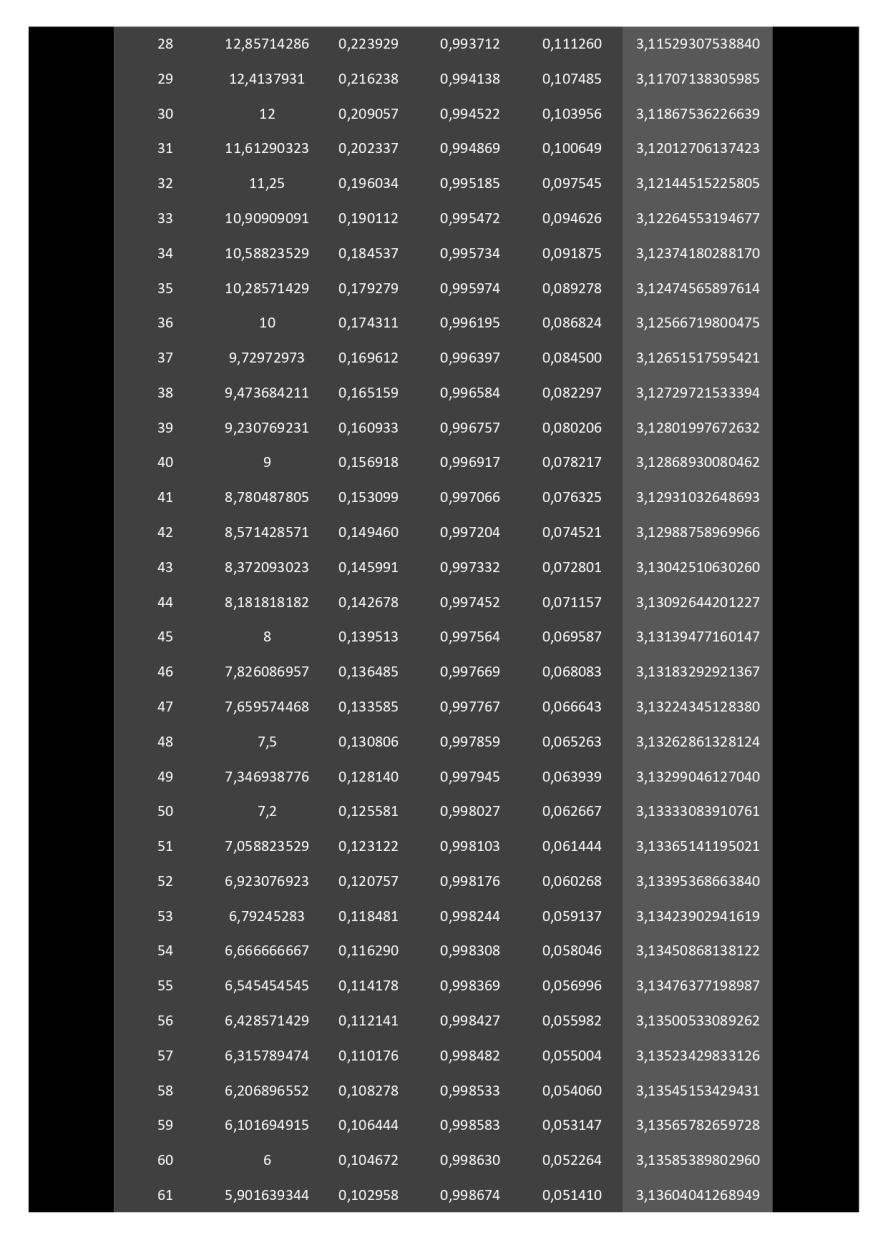
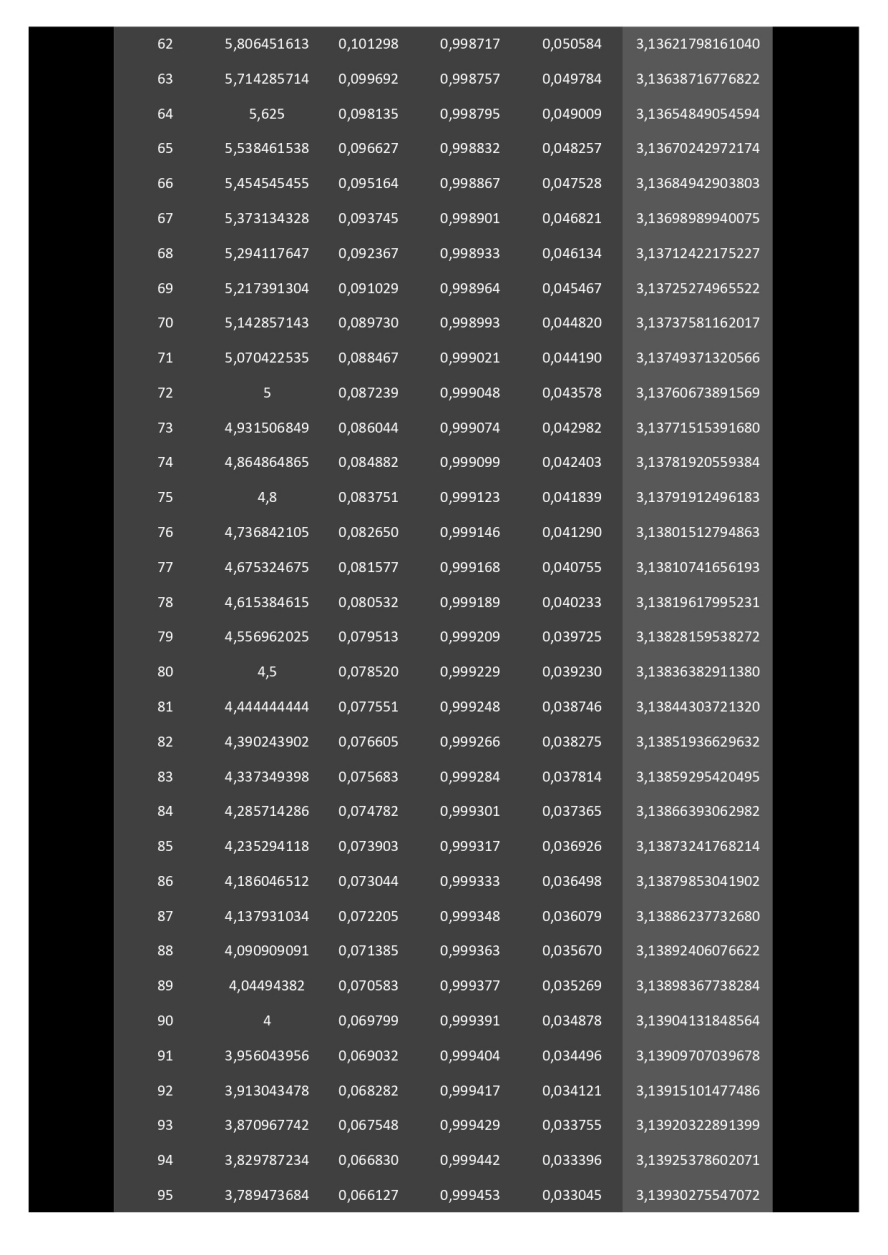
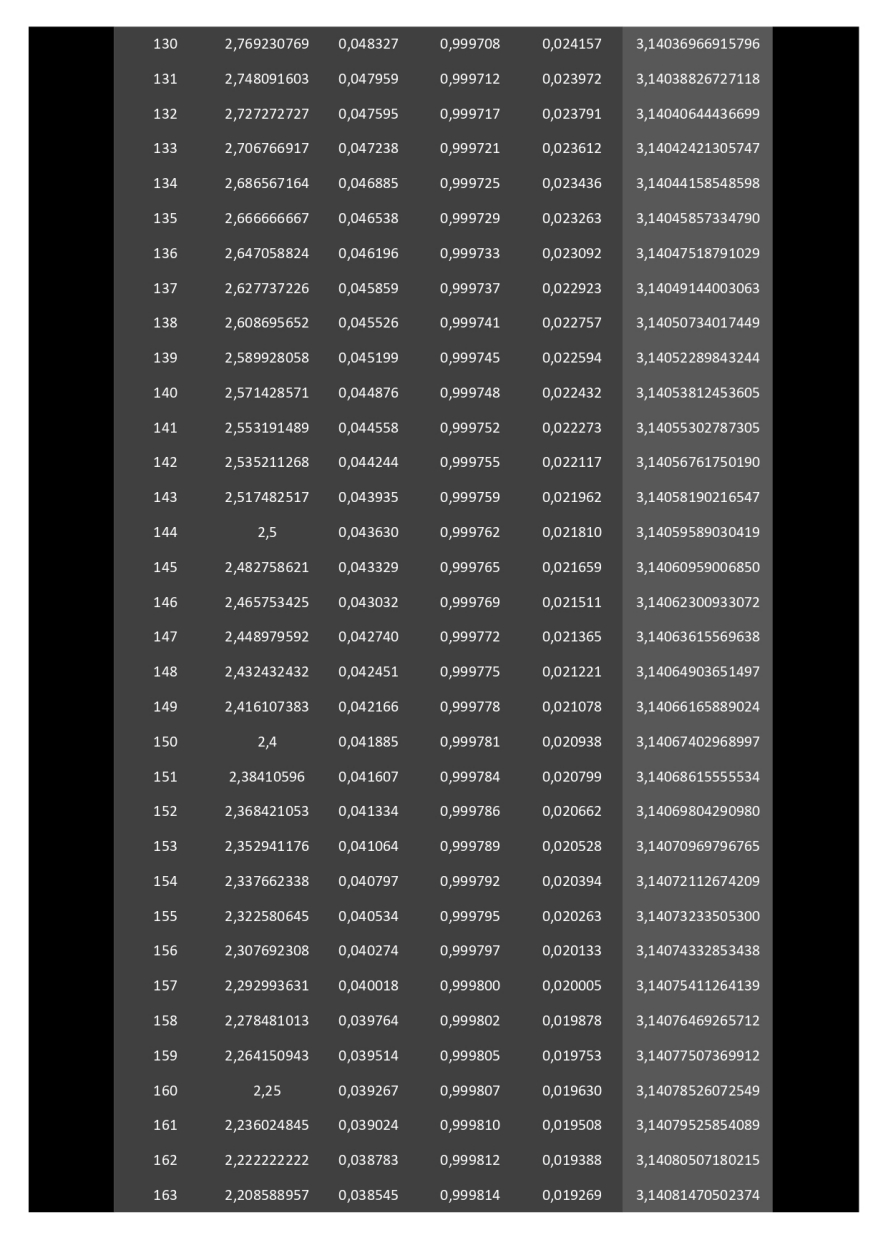
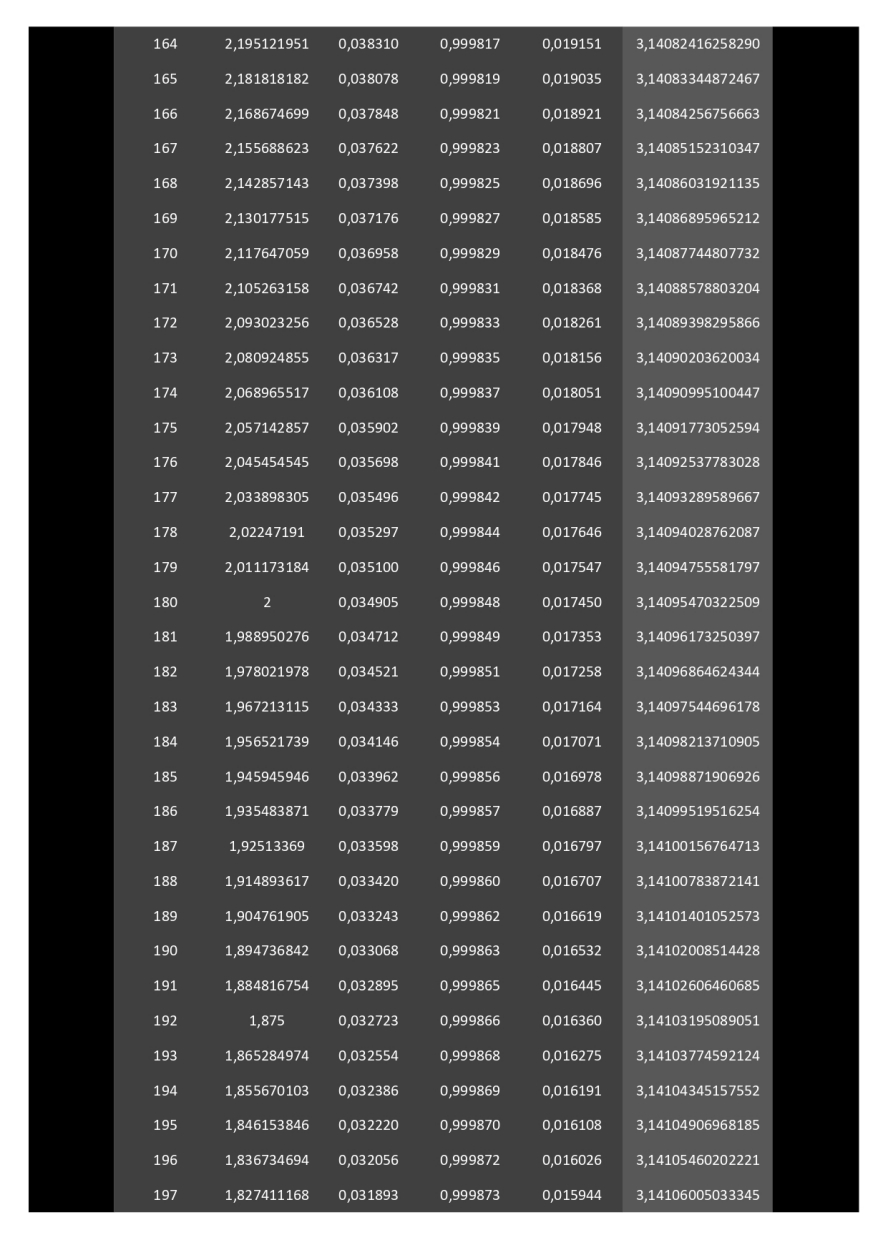
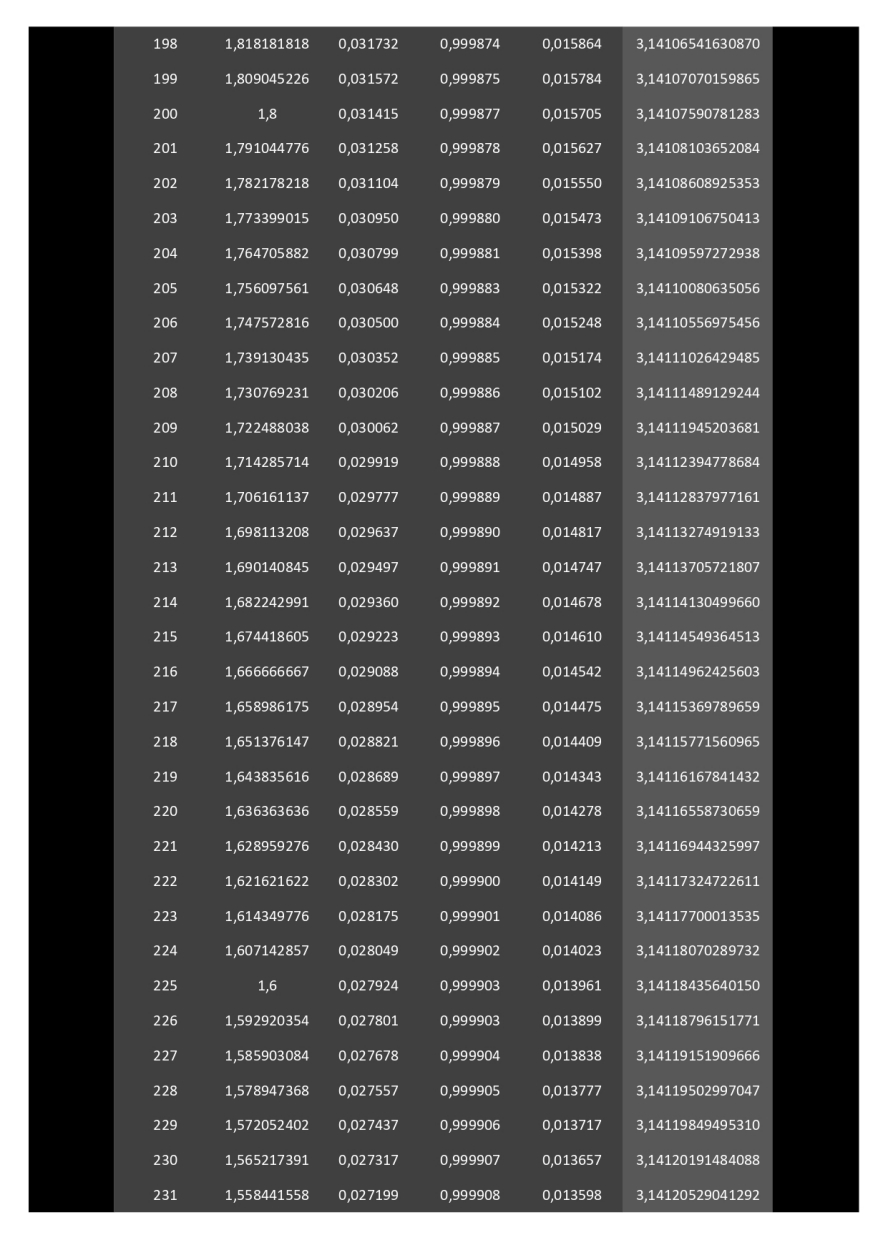
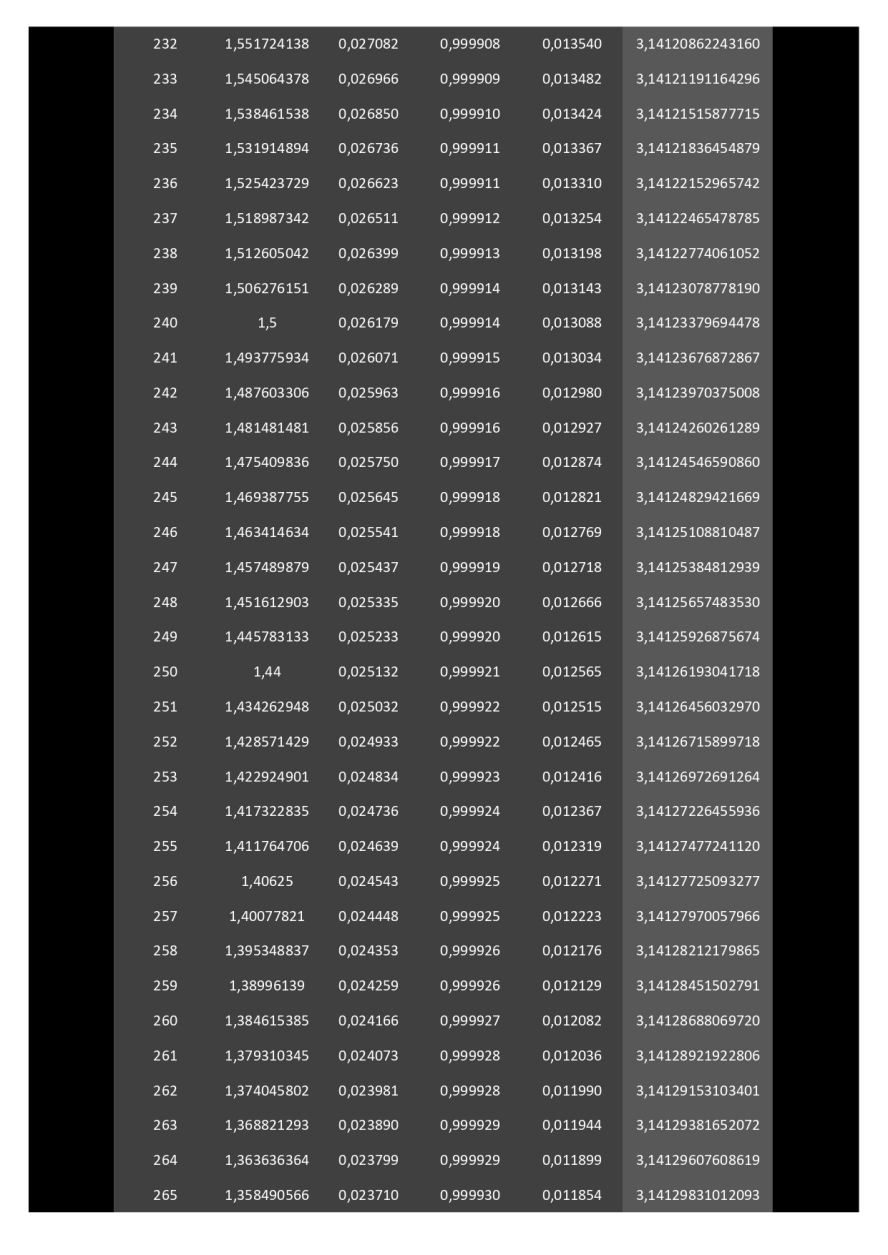
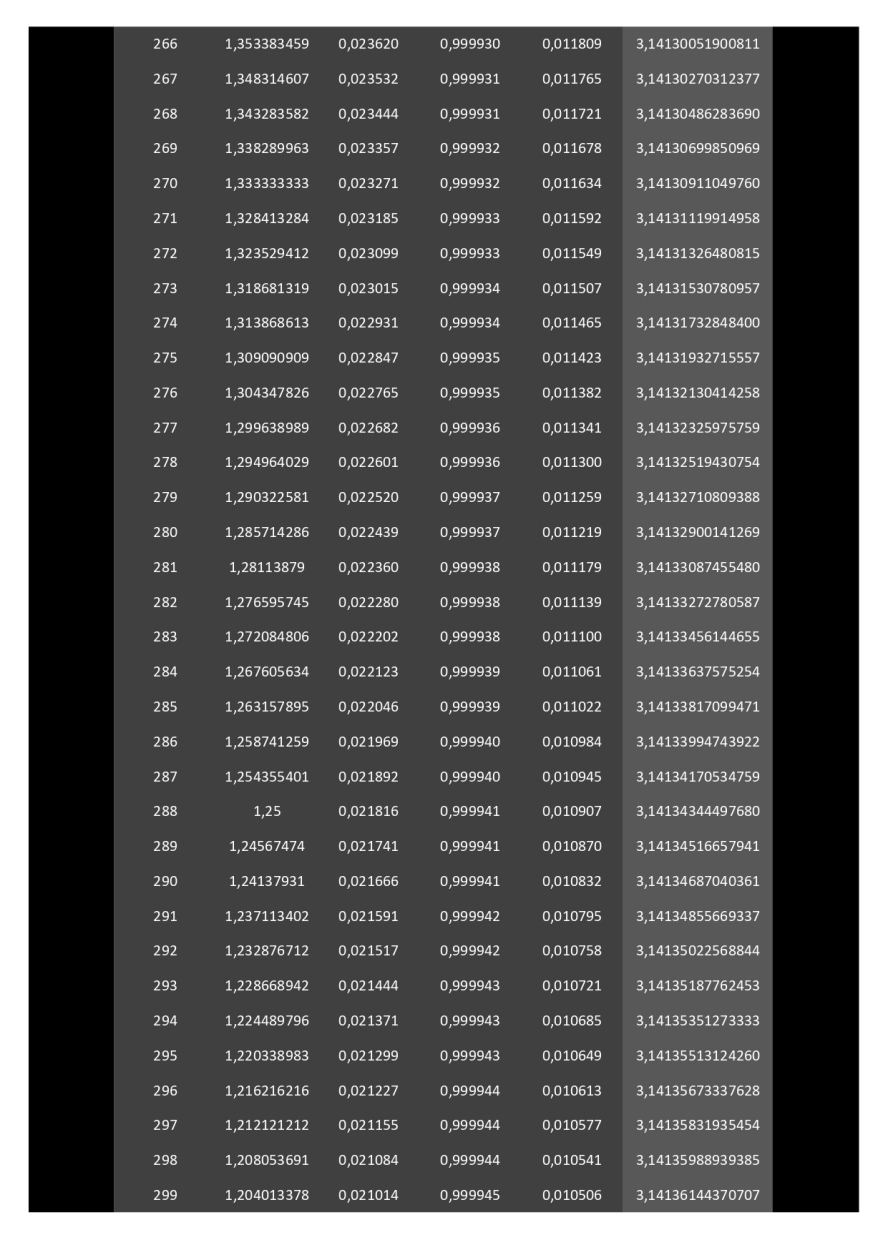
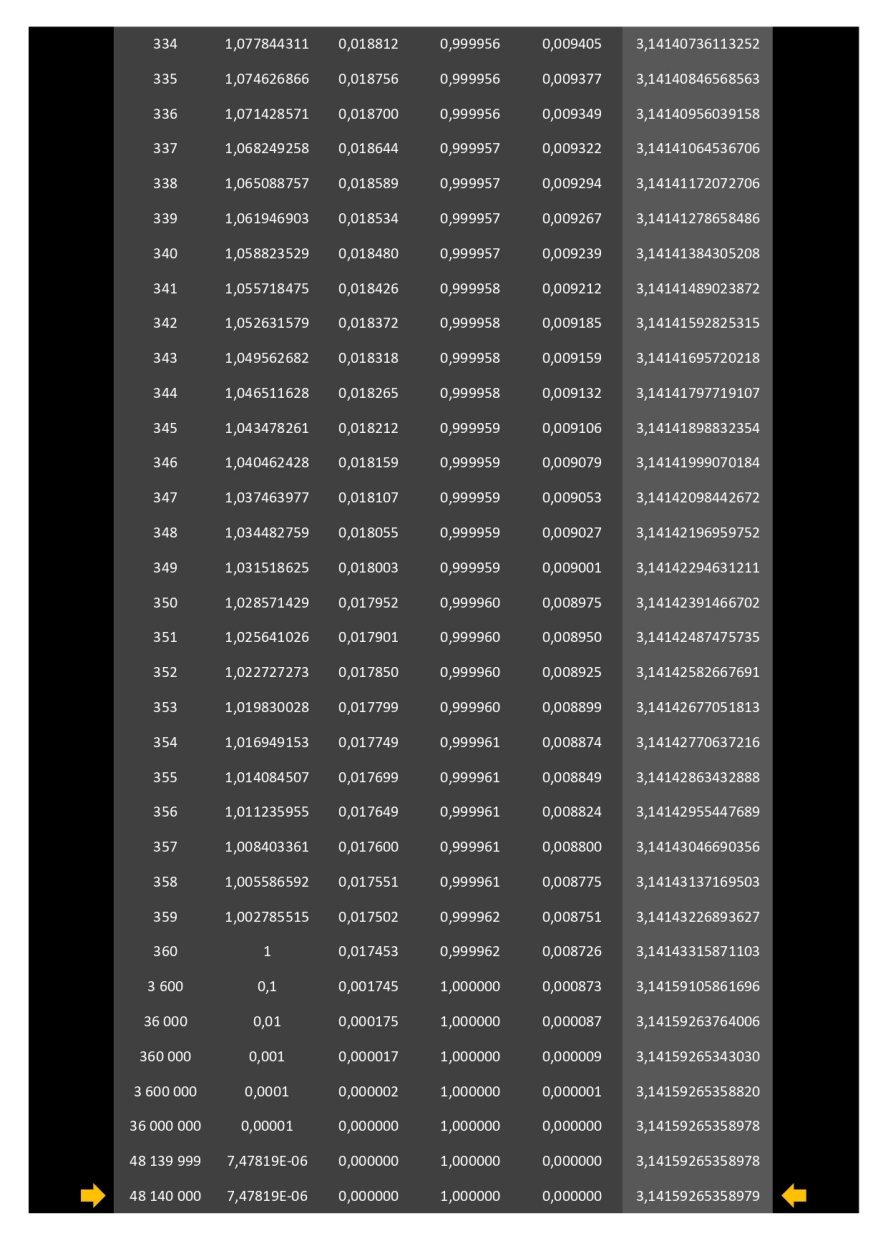
Ci-dessous, développé sur 11 pages, le calcul de la surface de polygones (à partir de 3 côtés) circonscrits dans un cercle de rayon 1.
• r = 1 (rayon du cercle)
• n = nombre de côtés du polygone (de 3 à 50 400 000)
• â = angle (en degrés) au sommet de chaque triangle
= 360/n
• c = longueur de chaque côté
= 2*r*sinus(â/2)
• h = hauteur de chaque triangle (apothème du polygone)
= racine_carrée(r²-(c/2)²)
• s = surface d'1 triangle
= (c*h)/2
• S = surface du polygone (tous les triangles)
= s*n
Note: comme r (rayon) = 1, alors
• c = 2*sinus(â/2)
• h = racine_carrée(1-(c/2)²)
--=O=--
Étapes des calculs:
• r = 1 (rayon du cercle)
• n = nombre de côtés du polygone (de 3 à 50 400 000)
• â = angle (en degrés) au sommet de chaque triangle
= 360/n
• c = longueur de chaque côté
= 2*r*sinus(â/2)
• h = hauteur de chaque triangle (apothème du polygone)
= racine_carrée(r²-(c/2)²)
• s = surface d'1 triangle
= (c*h)/2
• S = surface du polygone (tous les triangles)
= s*n
Note: comme r (rayon) = 1, alors
• c = 2*sinus(â/2)
• h = racine_carrée(1-(c/2)²)
--=O=--
C O N S T A T
C O N S T A T
Il faudra un polygone à 114 côtés pour donner l'aire du disque avec une précision de 2 chiffres après la virgule (3,14).
Il faudra un polygone à 48140000 côtés (quarante-huit millions cent quarante mille côtés) pour donner l'aire du disque avec une précision de 14 chiffres après la virgule (3,14159265358979).
Il faudra un polygone à 48140000 côtés (quarante-huit millions cent quarante mille côtés) pour donner l'aire du disque avec une précision de 14 chiffres après la virgule (3,14159265358979).
01
02
03

04
05
06
07
08
09

10
11

|

|

|
