
la loi
des cosinus
par le théorème
d'al-Kashi
des cosinus
par le théorème
d'al-Kashi

Le théorème d'al-Kashi (mathématicien et astronome perse né vers 1380 et mort en 1429) permet de généraliser le théorème de Pythagore aux triangles non rectangles (donc à tous les triangles).
Voici l'explication en images et commentaires.

Soit un triangle quelconque ABC:
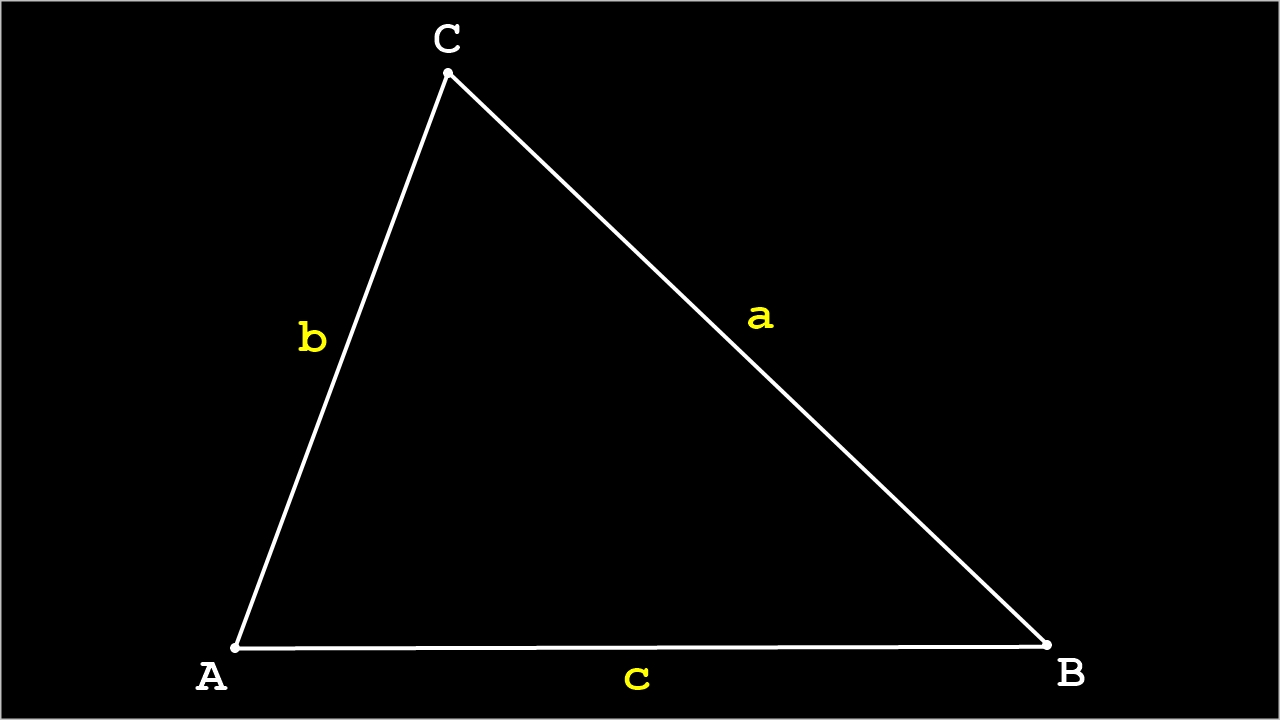
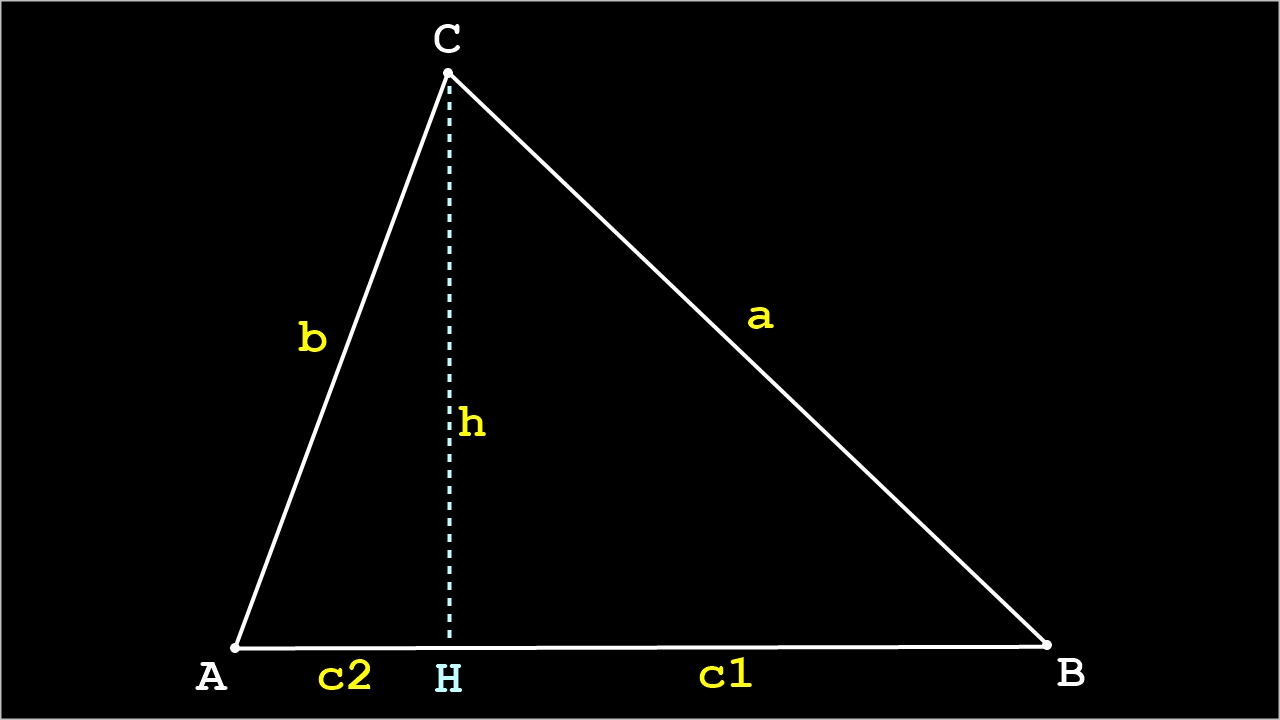
La hauteur depuis le sommet C divise le triangle quelconque en 2 triangles rectangles:
- le triangle BHC, rectangle en H et ayant a comme hypoténuse,
- le triangle AHC, rectangle en H et ayant b comme hypoténuse.
Le côté c, devient le côté c1 pour le triangle rectangle BHC et devient le côté c2 pour le triangle rectangle AHC (c1+c2=c).
Ce qui donne:
L'objectif est de calculer le côté a (ou BC).
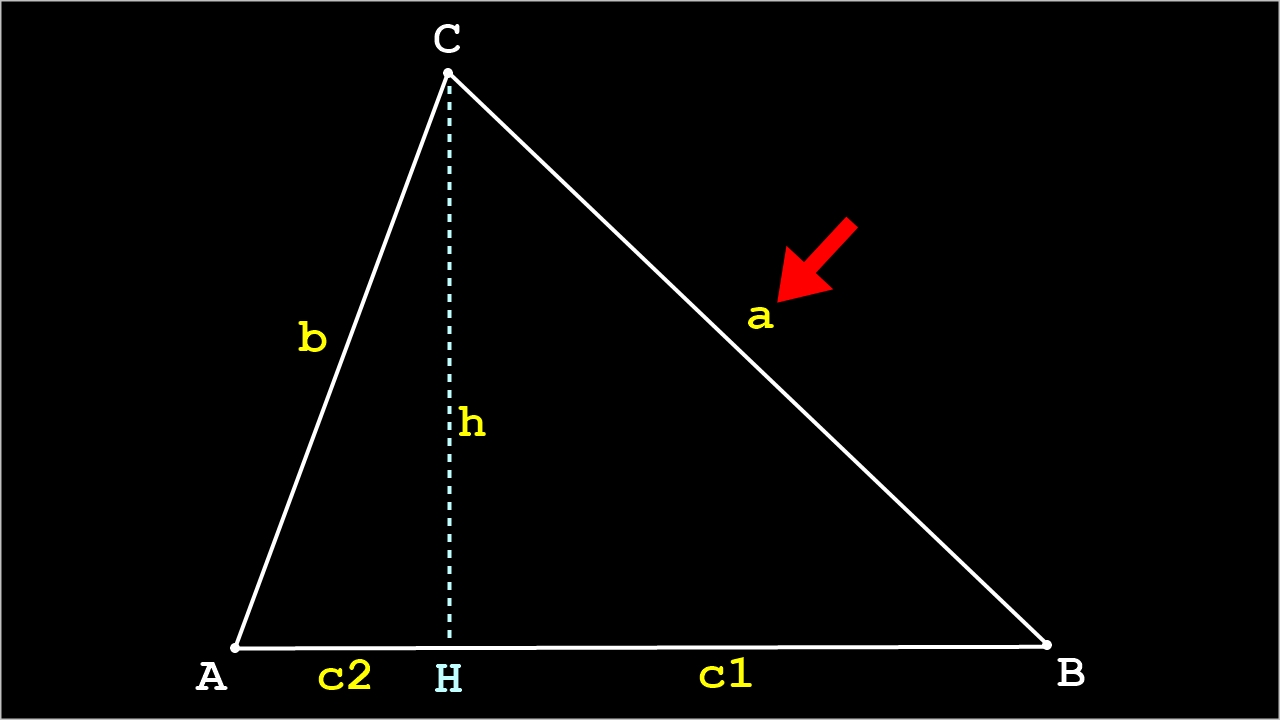
Démonstration:
Application du théorème de Pythagore sur le triangle rectangle BHC:
• a² = h²+c1²
Et sur le triangle rectangle AHC:
• b² = h²+c2²
qui peut également s'écrire:
• h² = b²-c2²
donc:
• a² = h²+c1²
devient:
• a² = b²-c2²+c1²
Puis, comme:
• c = c1+c2
peut aussi s'écrire:
• c1 = c-c2
donc:
• a² = b²-c2²+c1²
devient:
• a² = b²-c2²+(c-c2)²
qui se développe:
• a² = b²-c2²+c²-2c.c2+c2²
puis se simplifie:
• a² = b²+c²-2c.c2
Sachant que:
• cos(BAC) = c2/b
peut aussi s'écrire:
• c2 = b.cos(BAC)
a² devient alors:
• a² = b²+c²-2c.b.cos(BAC)
ou encore (résultat final):
• a² = b²+c²-2bc.cos(BAC)
Vérification:
• BC = a = ?
• AC = b = 16,21
• AB = c = 20
• BAC = 70°
• ABC = 46,5°
• ACB = 63,5°
(résultat attendu: a = 21)
• a² = b²+c²-2bc.cos(BAC)
• cos(70°) = 0,34202
• 2bc.cos(BAC) = 221,76576
• a² = 262,76+400-221,76576
• a² = 440,99 = 441
• √(441) = 21
• a est bien égal à 21
Deux remarques:
1) Dans l'exemple ci-dessus, l'angle BAC est égal à 70°.
Si l'angle BAC avait été égal à 90° (angle droit), son cosinus aurait été égal à 0 (cos(90) = 0) ...
et l'expression:
• a² = b²+c²-2bc.cos(BAC)
aurait alors été:
• a² = b²+c²-0
soit:
• a² = b²+c²
qui est l'application du théorème de Pythagore.
2) Cas d'un triangle quelconque avec l'angle BAC obtu (plus grand que 90°):
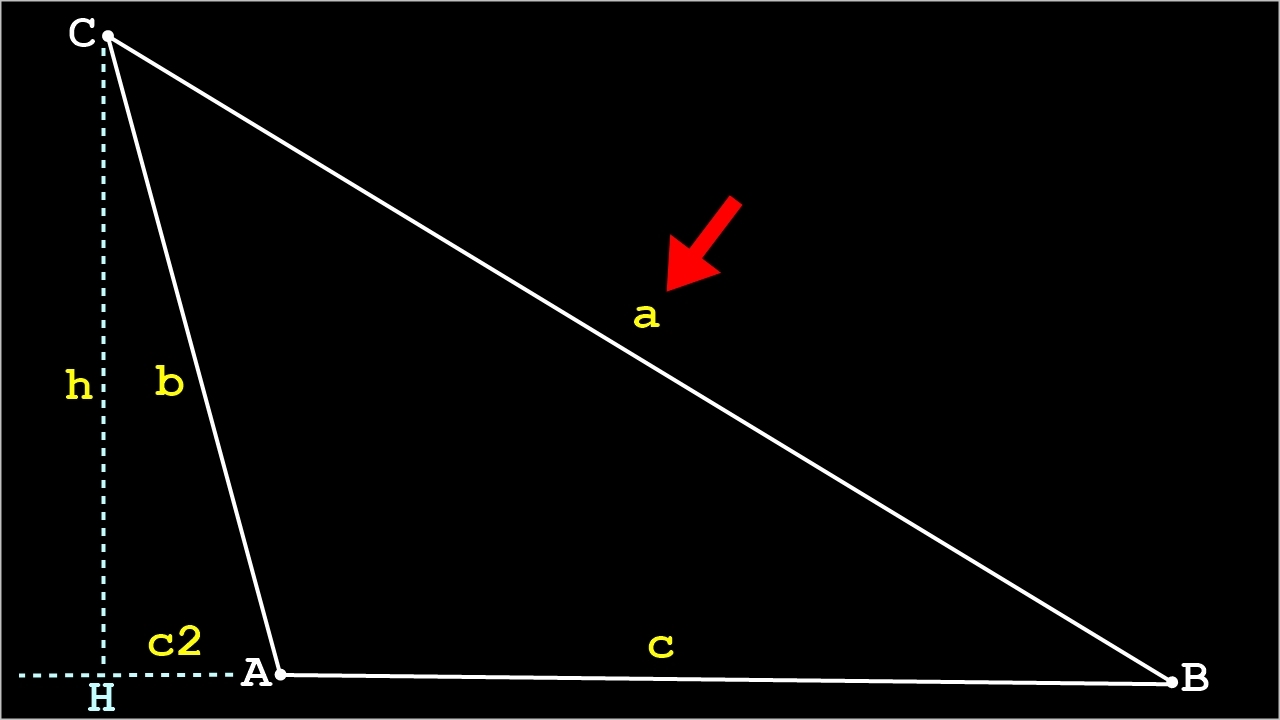
Démonstration:
• a² = h²+(c+c2)²
• b² = h²+c2²
• donc h² = b²-c2²
• donc a² = b²-c2²+(c+c2)²
• a² = b²-c2²+c²+2c.c2+c2²
• a² = b²+c²+2c.c2
• cos(CAH) = c2/b
• donc -cos(BAC) = c2/b (*)
• donc c2 = -b.cos(BAC)
• donc a² = b²+c²-2c.b.cos(BAC)
• donc a² = b²+c²-2bc.cos(BAC)
... exactement comme dans le premier exemple.
Vérification:
• BC = a = ?
• AC = b = 16,21
• AB = c = 20
• BAC = 110°
• ABC = 30,81°
• ACB = 39,19°
(résultat attendu: a = 29,74)
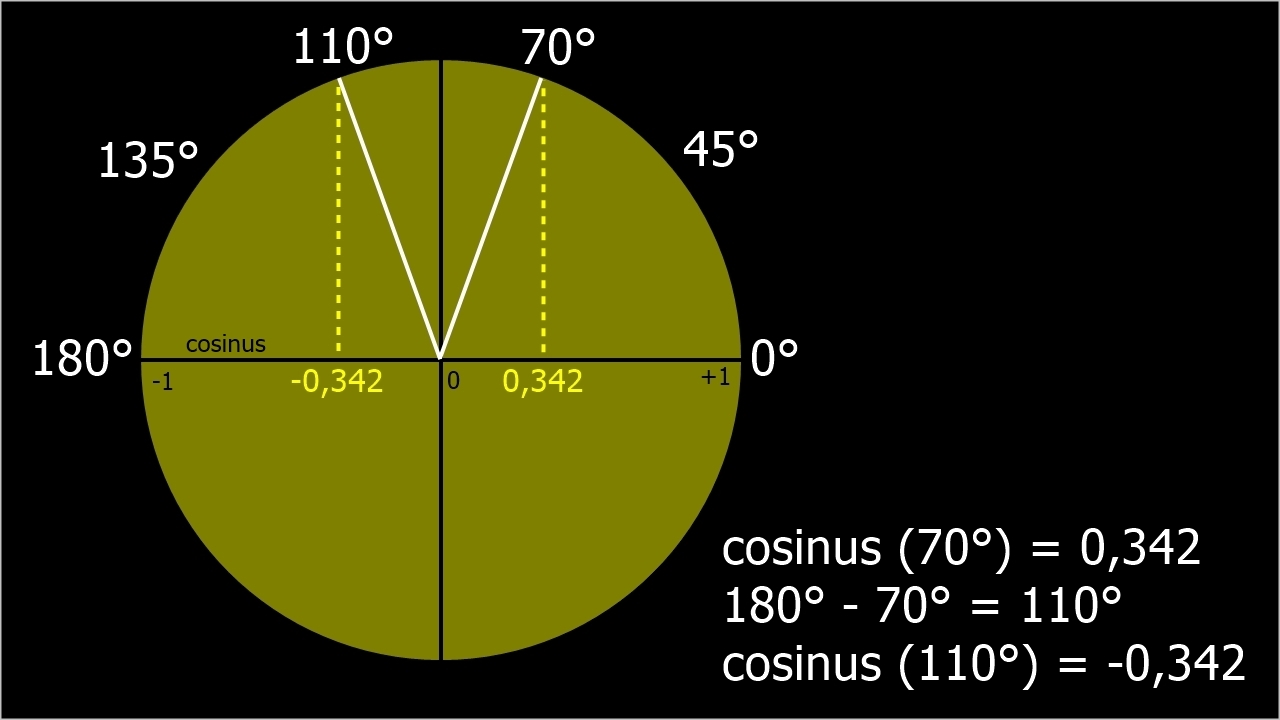
• cos(110°) = -0,342
• 2bc.-0,342 = -221,7528
• a² = 16,21²+20²-(-221,7528)
• a² = 262,7641+400+221,7528
= 884,5169
• √(884,5169) = 29,74
• a est bien égal à 29,74
(*) Note: 2 angles sont dits supplémentaires quand leur somme fait 180 degrés (angle plat). Dans ce cas, leurs cosinus sont opposés:
Synthèse:
Dans un triangle quelconque, à condition de connaître la dimmension de 2 côtés et la mesure de l'angle opposé au côté recherché, le théorème de Al Kashi propose les 3 formules suivantes:
• calcul du côté a:
• calcul du côté b:
• calcul du côté c:
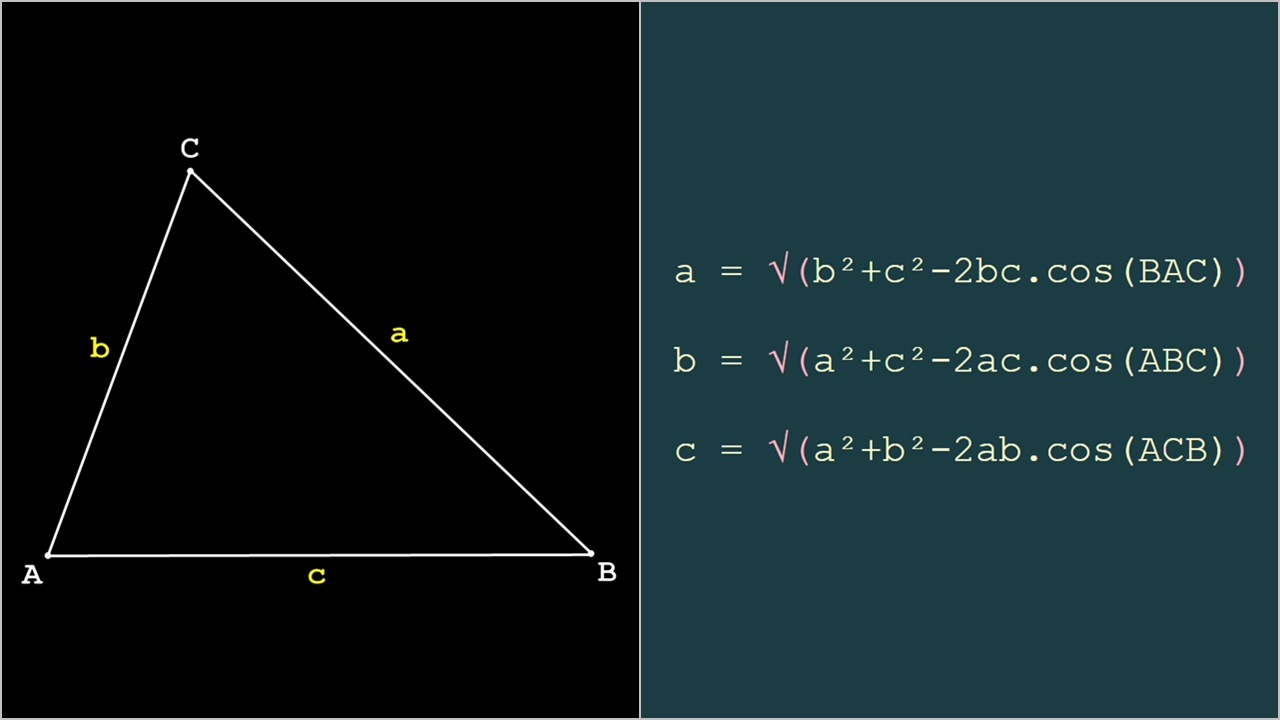

• • •
• •
•
• •
•
