i² = -1

Le contenu de cette page est d'aborder les nombres complexes à travers différentes rubriques relatives à ces nombres qui évoluent dans deux dimensions.
page créée le 9 février 2023
(dernière mise à jour: 10 février 2023)
(dernière mise à jour: 10 février 2023)

|

|

|
liste des rubriques

|

|

|
le concept du nombre i
La résolution de toutes les équations étaient impossibles aussitôt que se présentait une racine carrée d'un nombre négatif.
Pour contourner cet obstacle, un nouvel ensemble a été défini dans lequel il existe un nombre qui, élevé au carré, est égal à -1.
Ce nombre s'appelle i ("i" comme imaginaire) avec i² = -1 et, en conséquence, i = √(-1).
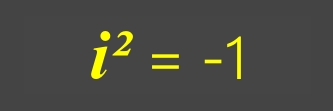
|
=> |
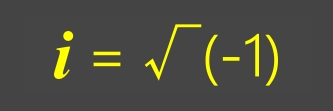
|
Ce nouvel ensemble est l'ensemble C, c'est-à-dire l'ensemble des nombres complexes dont l'unité est i.
Par exemple, +49 possède 2 racines carrées qui sont +7 et -7 car (+7)² = +49 et (-7)² = +49
Par contre, -49 ne peut pas posséder de racines carrées car aucun nombre multiplié par lui-même ne peut donner un résultat négatif, fondamentalement dans l'ensemble R.
Mais dans l'ensemble des nombres complexes (C) c'est possible. Exemple:
√(-49) = √(-1*49) = √(-1)*√(49) = i√(49) = i√(7²) = ± i7
Autres exemples:
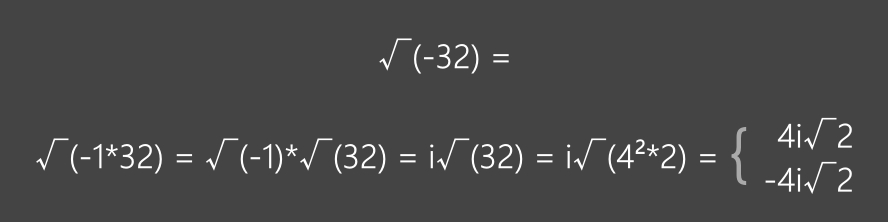
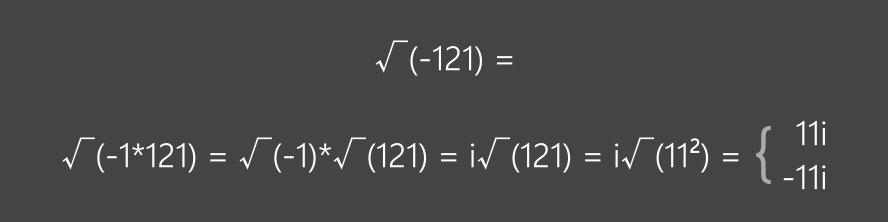
le nombre complexe
Soit à résoudre l'équation: x² + 2x + 4 = 0
• Δ = 2² - 4*1*4 = 4 - 16 = -12
• √Δ = √(-12) = √(2²*-3) = 2i√3
• racine 1: x = (-2 + 2i√3)/2 = -1 + i√3 (ou -1 + 1,732i)
• racine 2: x = (-2 - 2i√3)/2 = -1 - i√3 (ou -1 - 1,732i)
Le nombre -1 + i√3 est un nombre complexe composé d'une partie réelle (-1) et d'une partie imaginaire (i√3).
TOUS les nombres complexes sont sur un modèle: a + ib (a étant la partie réelle et ib la partie imaginaire).
Un nombre "simple" comme 4i√3 sera interprété comme 0 + 4i√3 sur le modèle de a + ib avec a = 0 et ib = 4i√3.
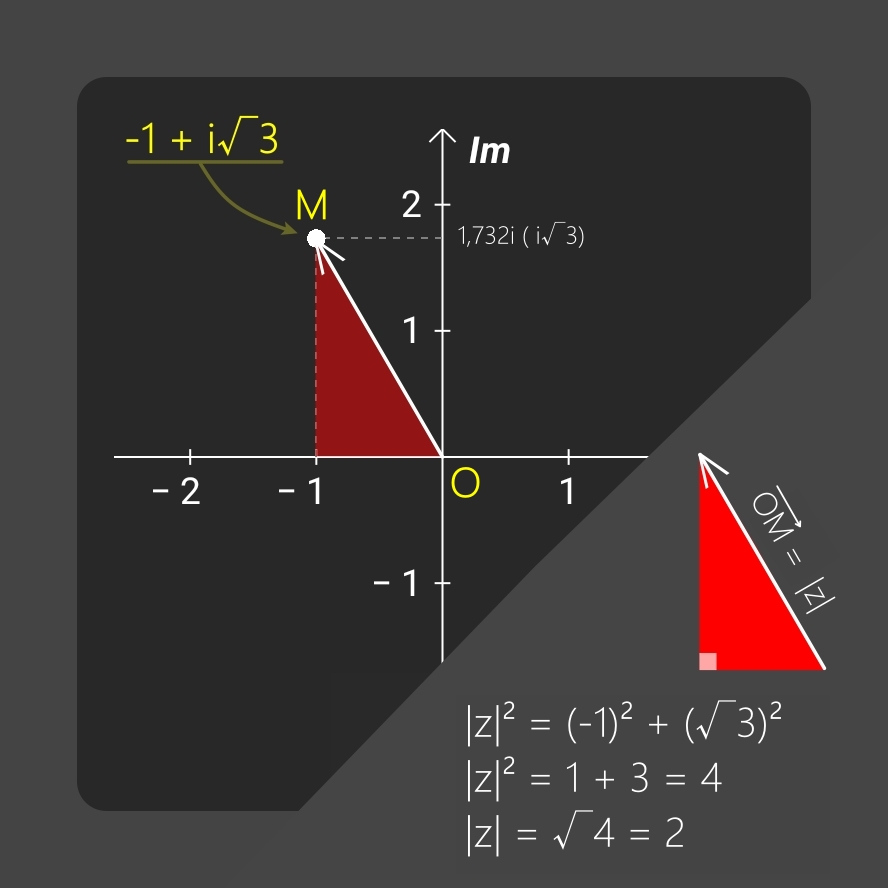
Reporter la première racine (-1 + i√3), de l'équation prise comme exemple, sur un repère cartésien orthogonal appelé également plan complexe permet de bien comprendre toute la subtilité des nombres complexes (image ci-dessous et commentaires ci-après):

Le plan complexe (ci-dessus) comprend l'axe des nombres réels (Re) et l'axe des nombres imaginaires (Im).
Le nombre complexe -1 + i√3 est le point dans l'espace du plan complexe aux coordonnées a = -1 de l'axe Re et ib = i√3 de l'axe Im.
module et argument
Occupant le plan complexe dans deux dimensions, les nombres complexes se comportent tels des vecteurs dans un espace vectoriel.
Chaque nombre complexe est identifiable à un vecteur dont l'origine est le point zéro appelé O (lettre O) du plan complexe et la destination un point appelé M. Les coordonnées du point M sont les valeurs a et b du nombre complexe.
Le vecteur OM est l'hypothénuse d'un triangle rectangle ayant a et b comme côtés de l'angle droit.
Ainsi, en appliquant le théorème de Pythagore, il est aisé de calculer la longueur du vecteur que l'on appelle module et qui est symbolisée par deux barres verticales.
Par exemple, le module du nombre complexe z = -1 + i√3 est:
• |z| = √(a² + b²)
• |z| = √[(-1)² + (√3)²]
• |z| = √(1 + 3)
• |z| = √(4)
• |z| = 2
Dans le plan complexe, l'angle du vecteur est avec le module (longueur du vecteur) l'autre élément essentiel pour caractériser la représentation graphique du nombre complexe.
Cet angle est appelé argument du nombre complexe.
L'argument est l'angle entre la demi-droite des nombres réels positifs et le module du nombre complexe.
Sachant qu'un nombre complexe est du type z = a + ib, la formule pour calculer l'argument est la suivante:
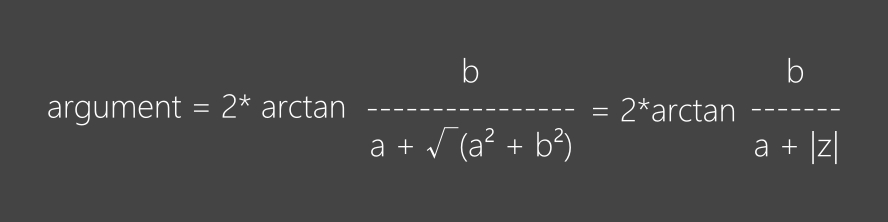
Exemples:
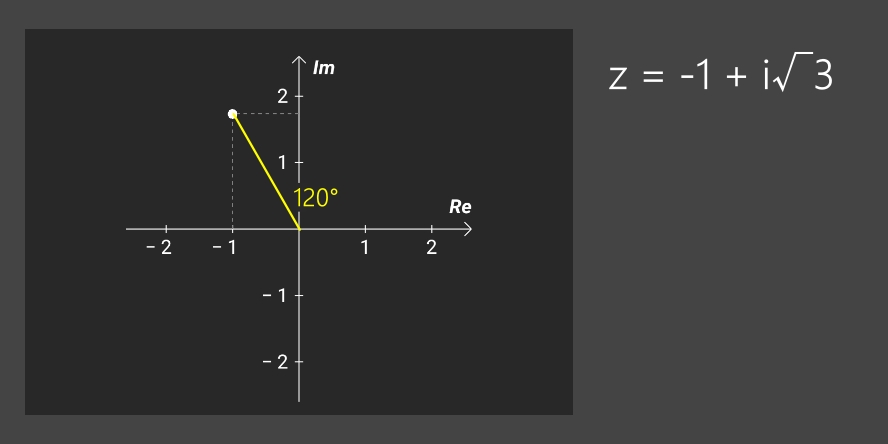
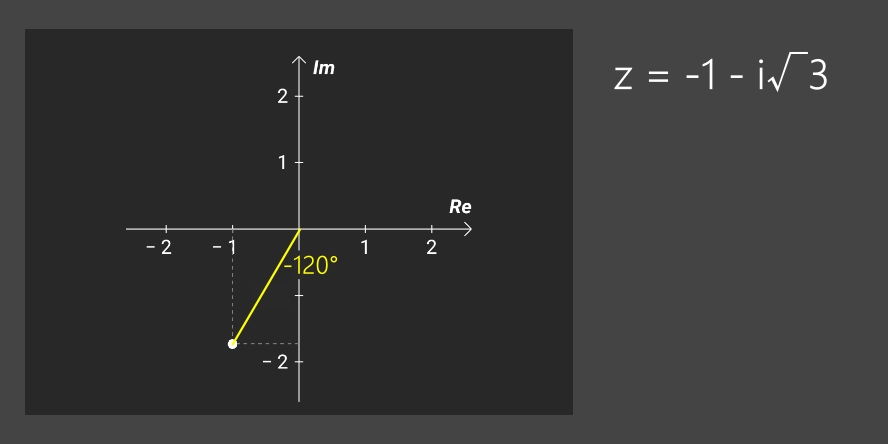
Note: les 4 exemples ci-dessous (calculs et, en suivant, les images correspondantes) couvrent les 4 quadrants du plan complexe.
• z = +1 + i√3 => arg(z) = 2*arctan[√3/(1 + 2)] = 60°
• z = -1 + i√3 => arg(z) = 2*arctan[√3/(-1 + 2)] = 120°
• z = -1 - i√3 => arg(z) = 2*arctan[-√3/(-1 + 2)] = -120°
• z = +1 - i√3 => arg(z) = 2*arctan[-√3/(1 + 2)] = -60°
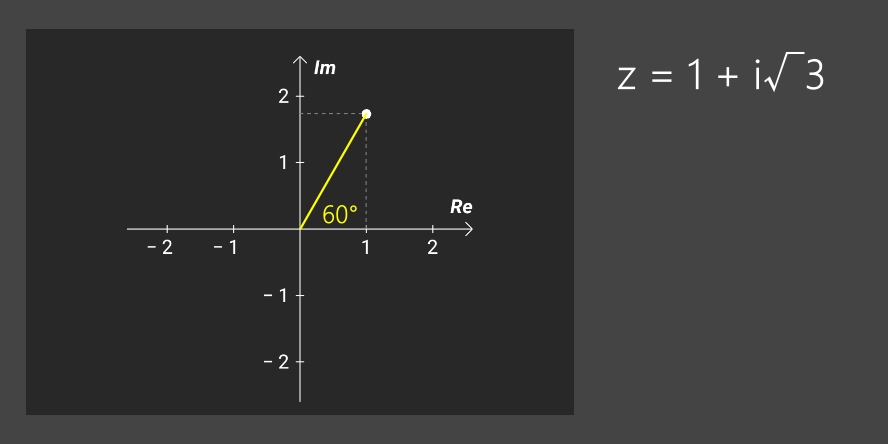
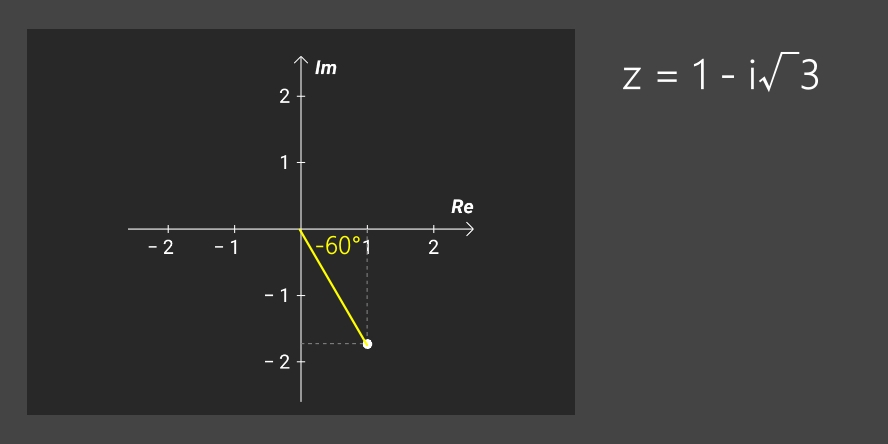
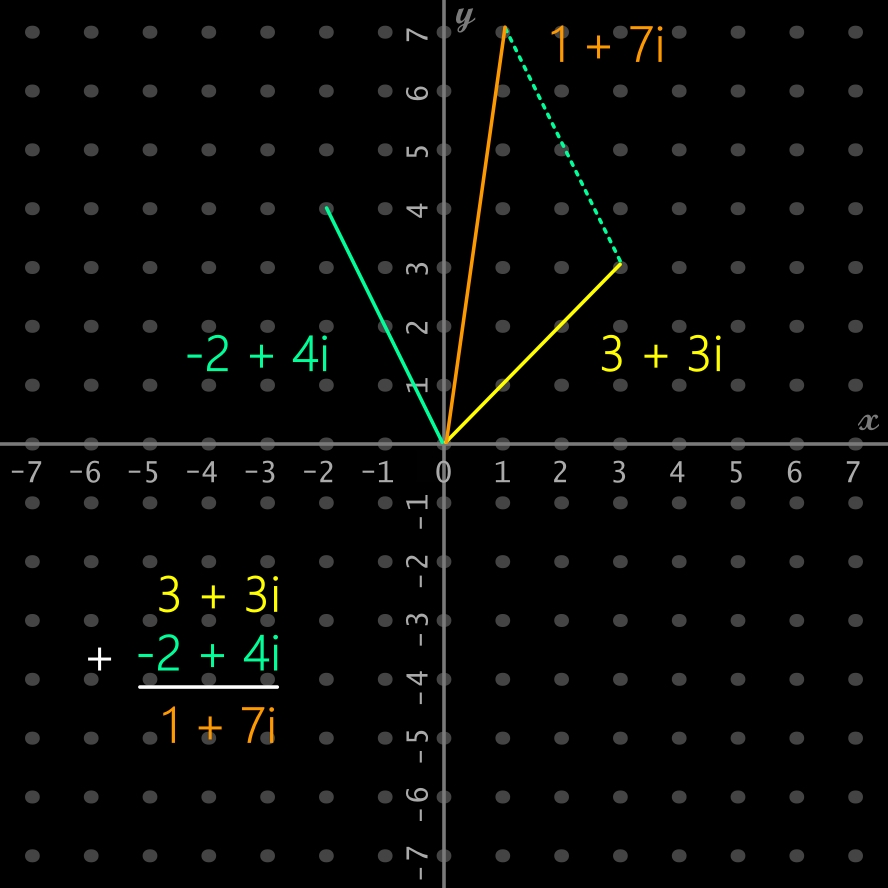
opérations simples: + - * /
Addition (ci-dessous): (3 + 3i) + (-2 + 4i)
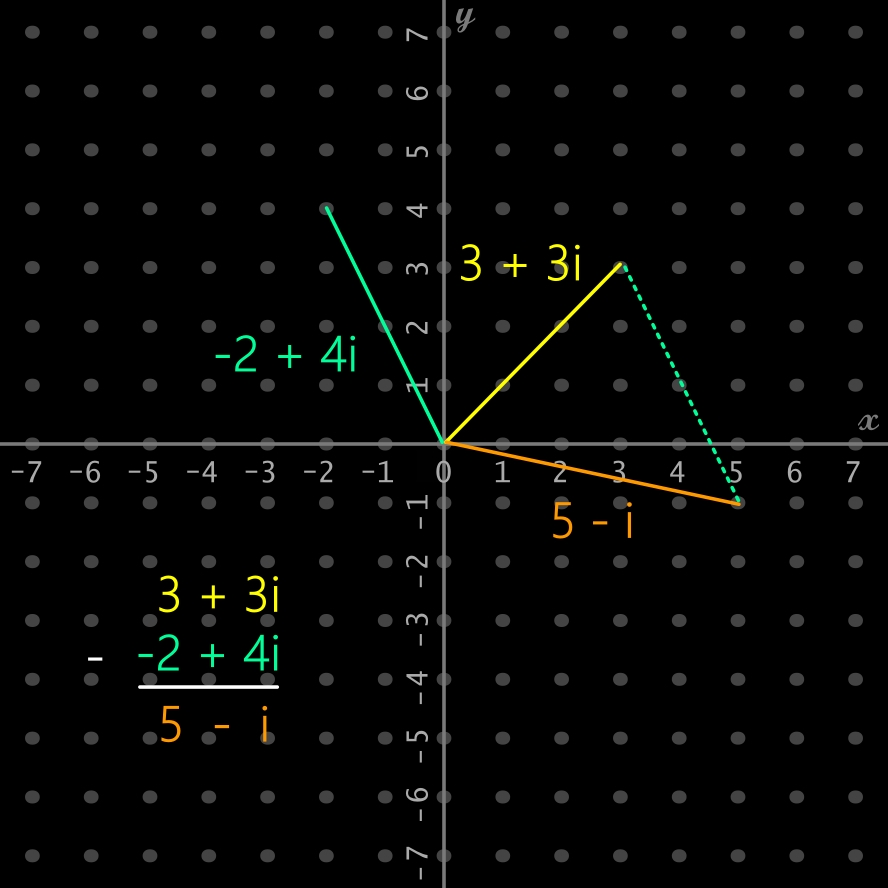
Soustraction (ci-dessous): (3 + 3i) - (-2 + 4i)
Multiplication par un réel (ci-dessous): (3 + 3i) * 2
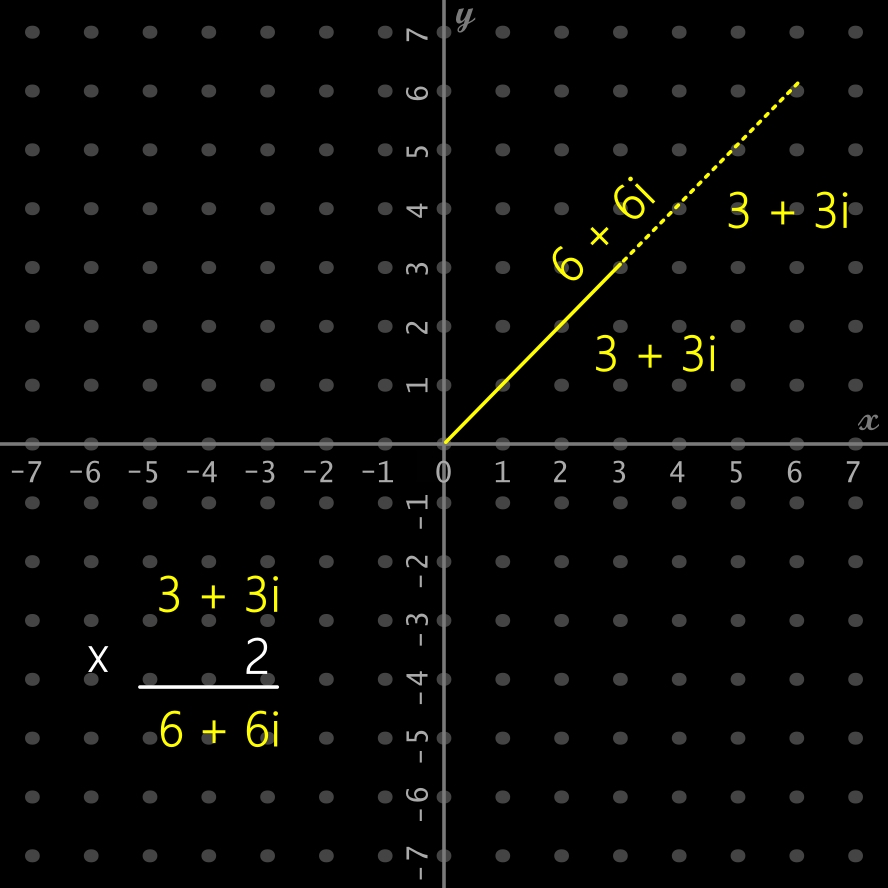
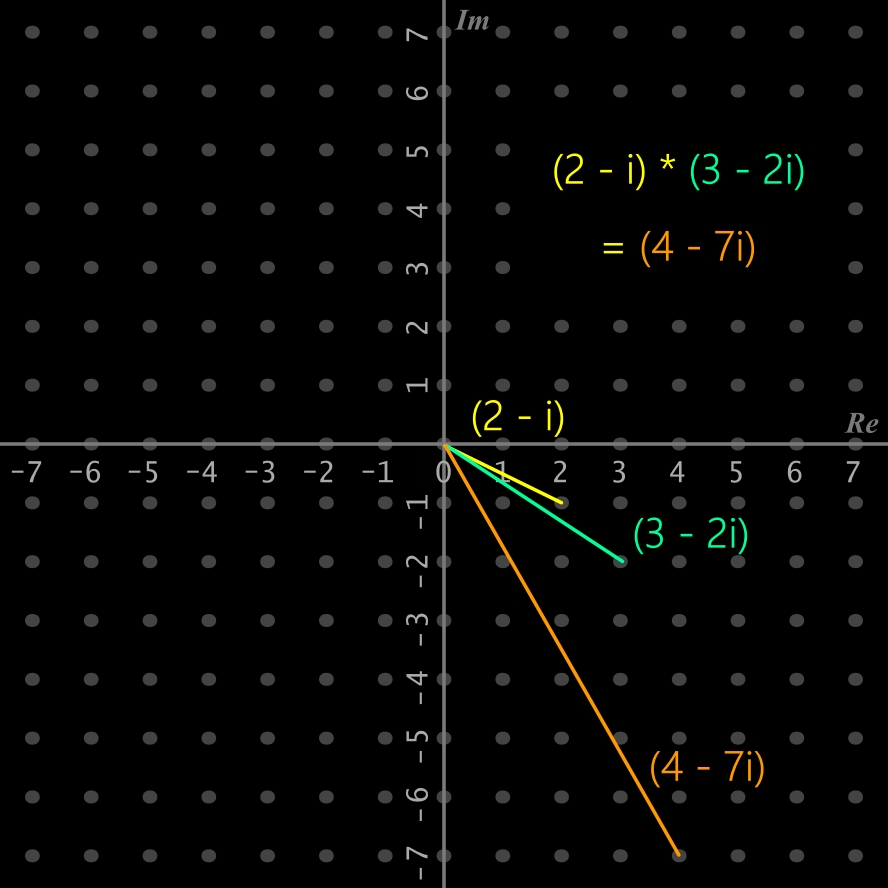
Multiplication entre 2 nombres complexes: (2 - i) * (3 - 2i)
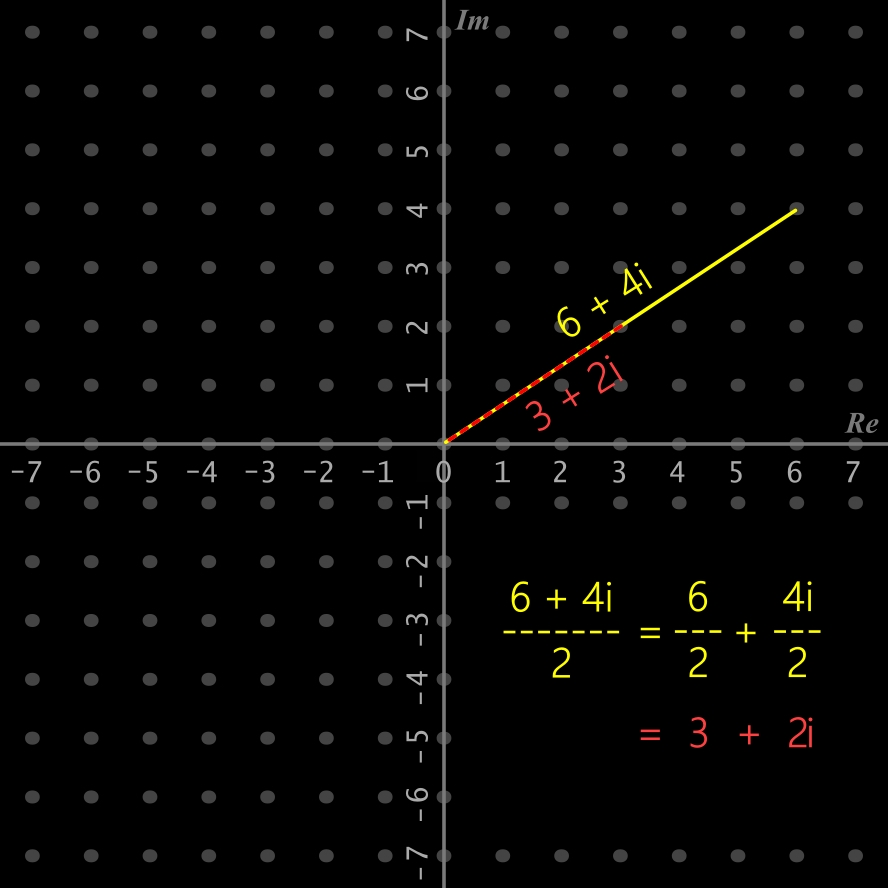
Division d'un nombre complexe par un réel: (6 + 4i) / 2
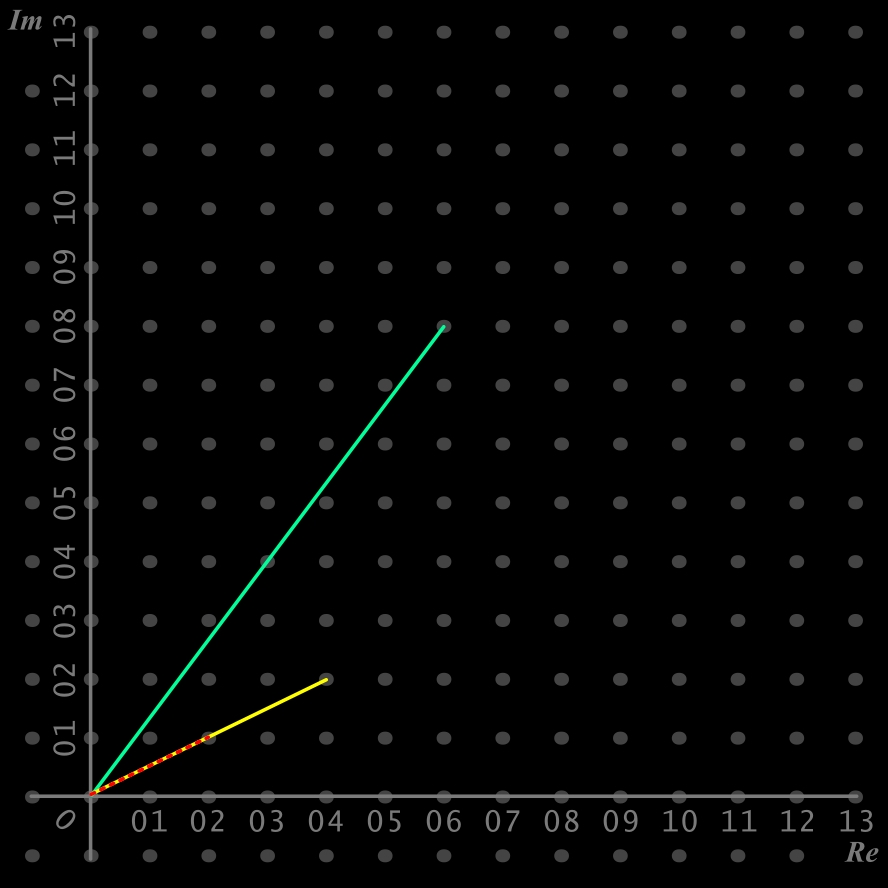
Division entre 2 nombres complexes: (6 + 8i) / (4 + 2i)
racine carrée (algébriquement)
- sans formule -
- sans formule -
Écrire √(i) n'a pas vraiment de sens car la fonction racine carrée n'est définie que dans l'ensemble des nombres réels (R). Et i n'est ni un réel et pas davantage un réel positif.
En conséquence, résoudre l'équation z² = i a plus de sens, et pour le même objectif, bien entendu.
On devrait même écrire, en toute rigueur, z² = 0 + 1i même si, dans pareil cas, c'est totalement neutre pour l'équation.
EXEMPLE 1 - Résolution de l'équation z² = i:
• z² = i
• remplacer z par son expression algébrique:
• (a + ib)² = i
• développer:
• a² + 2abi + (ib)² = i
• a² + 2abi + i²b² = i
• a² + 2abi + (-1)b² = i
• a² + 2abi - b² = i
• regrouper les termes réels:
• (a² - b²) + 2abi = i
• (a² - b²) + 2abi - i = 0
• (a² - b²) + i(2ab - 1) = 0
• noter: si z = 0 => les 2 parties (Re et Im) = 0
• z = 0 <=> Re(z) = 0 et Im(z) = 0
• en conséquence ...
• (a² - b²) + i(2ab - 1) = 0
• devient le système (2 lignes):
• L1 (ligne 1): (a² - b²) = 0
• L2 (ligne 2): (2ab - 1) = 0
• L2:
• 2ab - 1 = 0
• ab = 1/2
• b = (1/2)/a
• b = 1/(2a)
• remplacer b par 1/2a dans L1:
• a² - (1/2a)² = 0
• a² - 1/4a² = 0
• 4a⁴/a² - 1/4a² = 0
• (4a⁴ - 1)/4a² = 0
• une fraction est nulle dès que son numérateur est nul,
• en conséquence (4a4 - 1)/4a² = 0 devient:
• 4a⁴ - 1 = 0
• a⁴ - 1/4 = 0
• (a²)² - (1/2)² = 0
• (a² - 1/2)(a² + 1/2) = 0
• (a² + 1/2) ne peut pas être nul, en conséquence
• (a² - 1/2)(a² + 1/2) = 0 devient:
• a² - 1/2 = 0
• (a - 1/√2)(a + 1/√2) = 0
• obtenir a (2 solutions):
• (a - 1/√2) = 0 => a = 1/√2 = √2/2
• (a + 1/√2) = 0 => a = -1/√2 = -√2/2
• obtenir b (2 solutions):
• b = 1/(2a) et a = 1/√2 => b = 1/(2*1/√2) = √2/2
• b = 1/(2a) et a = -1/√2 => b = -1/(2*1/√2) = -√2/2
• résultats finaux (image ci-dessous):
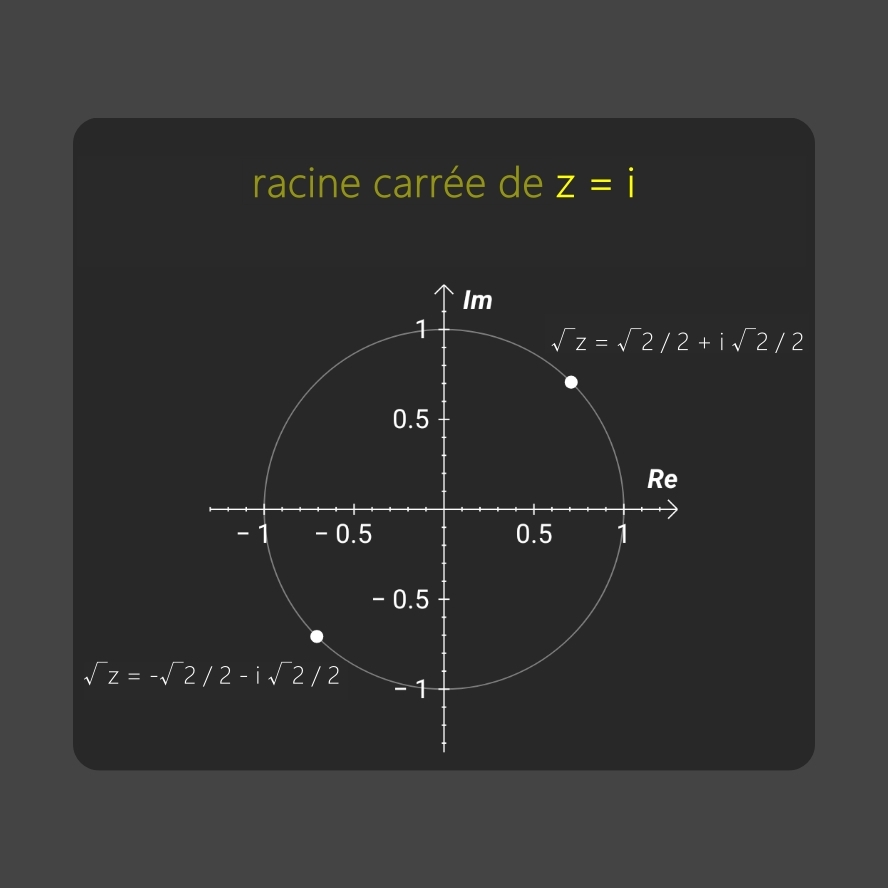
Vérification:
• √z = (√2/2 + i√2/2)
• (√z)² = (√2/2 + i√2/2)²
• z = (√2/2 + i√2/2)²
• z = (√2/2)² + 2*√2/2*i√2/2 + (i√2/2)²
• z = 1/2 + √2*i√2/2 + i²/2
• rappel important: i² = -1
• z = 1/2 + i - 1/2
• z = i
• √z = (-√2/2 - i√2/2)
• (√z)² = (-√2/2 - i√2/2)²
• z = (-√2/2 - i√2/2)²
• z = (-√2/2)² - 2*-√2/2*i√2/2 + (i√2/2)²
• z = 1/2 + √2*i√2/2 + i²/2
• rappel important: i² = -1
• z = 1/2 + i - 1/2
• z = i
EXEMPLE 2 - Résolution de l'équation z² = -5 + 12i:
• z² = -5 + 12i
• remplacer z par son expression algébrique:
• (a + ib)² = -5 + 12i
• développer:
• a² + 2abi + (ib)² = -5 + 12i
• a² + 2abi + i²b² = -5 + 12i
• a² + 2abi + (-1)b² = -5 + 12i
• a² + 2abi - b² = -5 + 12i
• regrouper les termes réels:
• (a² - b²) + 2abi = -5 + 12i
• (a² - b²) + 2abi + 5 - 12i = 0
• (a² - b²) + 5 + 2abi - 12i = 0
• (a² - b²) + 5 + i(2ab - 12) = 0
• noter: si z = 0 => les 2 parties (Re et Im) = 0
• z = 0 <=> Re(z) = 0 et Im(z) = 0
• en conséquence (a² - b²) + 5 + i(2ab - 12) = 0
• devient le système (2 lignes):
• L1 (ligne 1): a² - b² + 5 = 0
• L2 (ligne 2): 2ab - 12 = 0
• L2:
• 2ab - 12 = 0
• 2ab = 12
• ab = 12/2
• ab = 6
• b = 6/a
• => L1 devient:
• a² - (6/a)² + 5 = 0
• a² - 36/a² + 5 = 0
• a²(a² - 36/a² + 5) = 0*a²
• a²*a² - a²*(36/a²) + a²*5 = 0
• a⁴ - 36 + 5a² = 0
• a⁴ + 5a² - 36 = 0
• si X = a² alors a⁴ + 5a² - 36 = 0 devient:
• X² + 5X - 36 = 0
• delta = 25 - 4*1*(-36) = 25 + 144 = 169
• √(delta) = √169 = 13
• racine #1: X = (-5 + 13)/2 = 8/2 = 4
• racine #2: X = (-5 - 13)/2 = -18/2 = -9
• a² = X => a = √X
• racine pour X = 4: a = √4 = 2 et -2
• racine pour X = -9: pas de solution car a est un réel
• comme b = 6/a (voir plus haut)
• racine pour a = 2: b = 6/a => b = 6/2 => b = 3
• racine pour a = -2: b = 6/a => b = 6/-2 => b = -3
• résultats finaux (image ci-dessous):
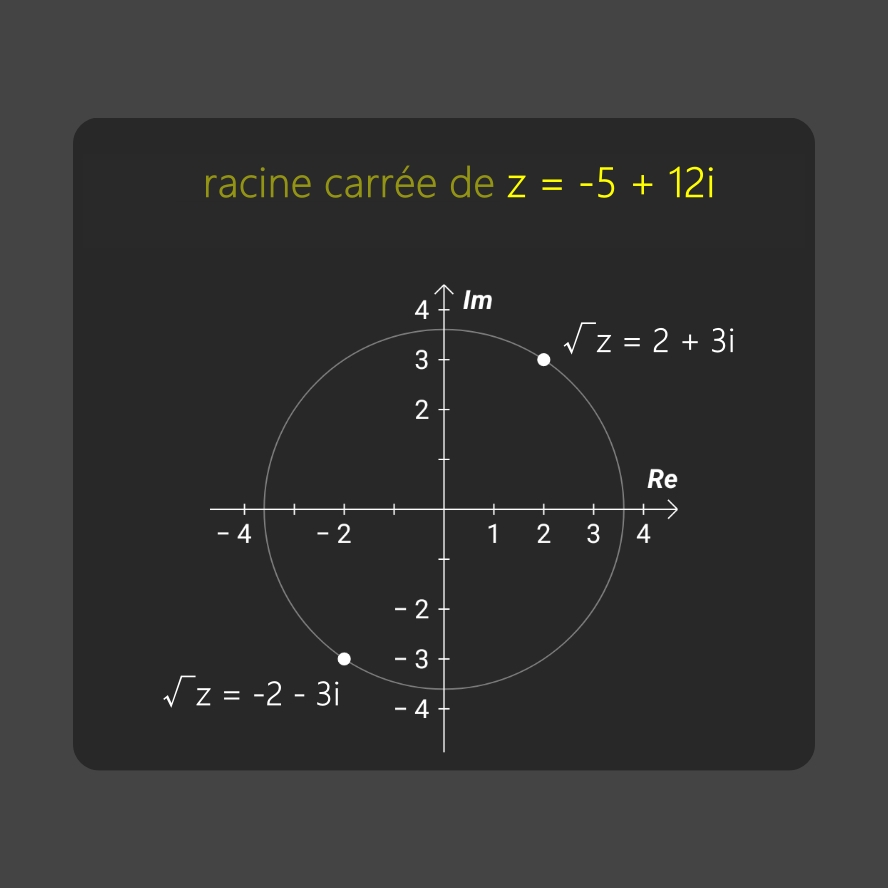
Vérification:
• √z = (2 + 3i)
• (√z)² = (2 + 3i)²
• z = (2 + 3i)²
• z = 2² + 2*2*3i + (3i)²
• z = 4 + 12i + 3²*i²
• rappel important: i² = -1
• z = 4 + 12i + 9*-1
• z = 4 + 12i - 9
• z = -5 + 12i
• √z = (-2 - 3i)
• (√z)² = (-2 - 3i)²
• z = (-2 - 3i)²
• z = (-2)² - 2*-2*3i + (3i)²
• z = 4 + 12i + 3²*i²
• rappel important: i² = -1
• z = 4 + 12i + 9*-1
• z = 4 + 12i - 9
• z = -5 + 12i
racine carrée (algébriquement)
- avec formule -
- avec formule -
La formule est la suivante:

racine carrée (géométriquement)
Calculer la racine carrée d'un nombre complexe en utilisant les propriétés géométriques d'un tel nombre est très simple puisqu'il suffit de multiplier la racine carrée de son module par le cosinus et par le sinus de la moitié de son argument.
Soit à calculer la racine carrée d'un nombre z avec mod son module, arg son argument, et Re + Im ses parties réelle et imaginaire. Procédure (en 5 étapes):
1) identifier le module de z: mod
2) identifier l'argument de z: arg
3) Re = √(mod) multiplié par le cosinus de arg/2
4) Im = √(mod) multiplié par le sinus de arg/2
5) pour obtenir: √(z) = Re + Imi
Exemple: calcul de la racine carrée de z = (-5 + 12i)
• z = (-5 + 12i)
• mod(z) = √((-5)² + 12²) = 13
• arg(z) = 2*arctan(12/(-5 + 13)) = 112,61°
• Re = √13*cos(112,61/2) = 2
• Im = √13*isin(112,61/2) = 3i
• √z = Re + Im
• √z = (2 + 3i)
Ci-dessous, le même calcul en image dans le plan complexe:
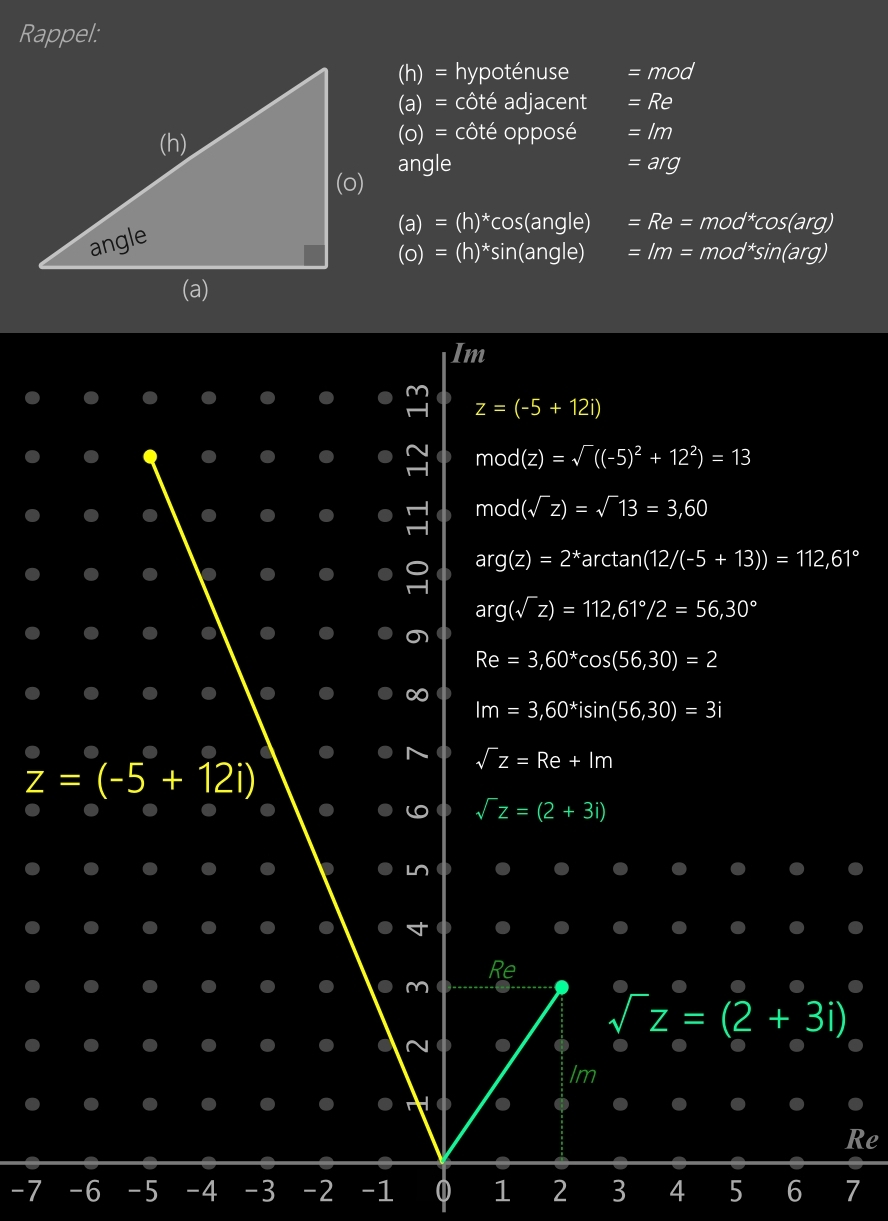
ATTENTION:
Tout nombre complexe (non nul) possède 2 racines carrées opposées. Ainsi z = (-5 + 12i) possède 2 racines carrées: (2 + 3i) et son opposé (-2 - 3i) (voir image ci-dessous).
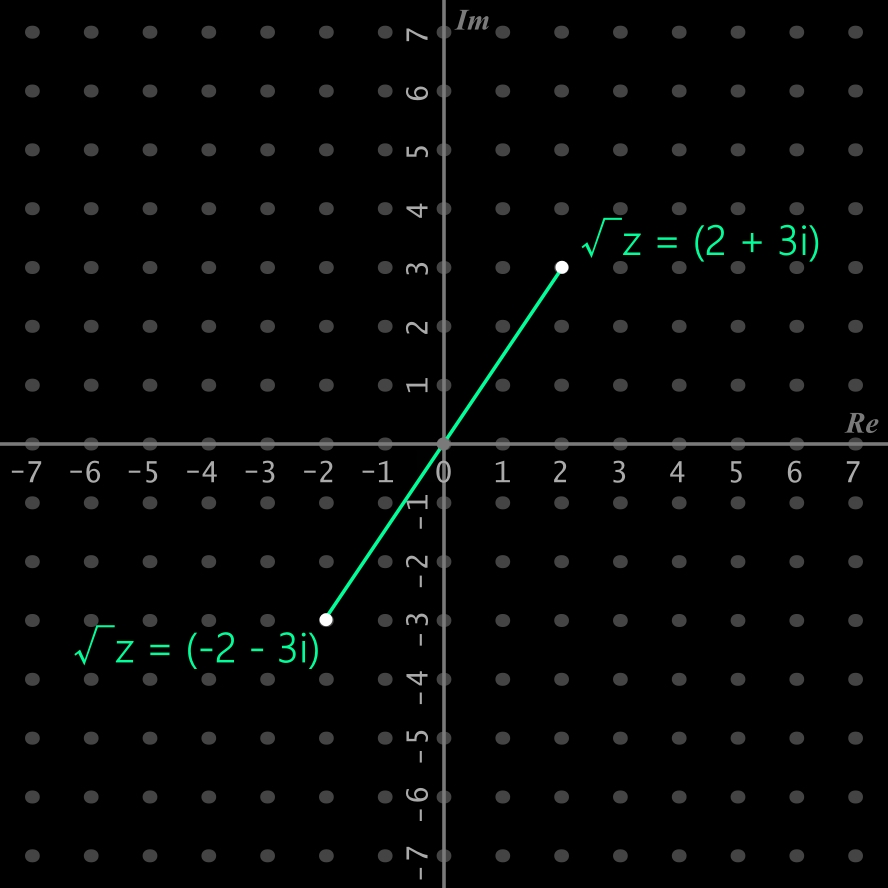
Vérification:
• √z = (2 + 3i)
• (√z)² = (2 + 3i)²
• z = (2 + 3i)²
• z = 2² + 2*2*3i + (3i)²
• z = 4 + 12i + 3²*i²
• rappel important: i² = -1
• z = 4 + 12i + 9*-1
• z = 4 + 12i - 9
• z = -5 + 12i
• √z = (-2 - 3i)
• (√z)² = (-2 - 3i)²
• z = (-2 - 3i)²
• z = (-2)² - 2*-2*3i + (3i)²
• z = 4 + 12i + 3²*i²
• rappel important: i² = -1
• z = 4 + 12i + 9*-1
• z = 4 + 12i - 9
• z = -5 + 12i
forme exponentielle
(application et démonstration)
(application et démonstration)
La forme géométrique (qui est une autre façon de dire forme trigonométrique) et la forme exponentielle sont les mêmes. C'est simplement une question de notation. La forme exponentielle est beaucoup plus pratique que la forme trigonométrique pour effectuer des calculs car la forme exponentielle permet d'utiliser les formules et les propriétés des puissances.
Pour passer de la forme trigonométrique à la forme exponentielle, il faudra appliquer la formule de Leonhard EULER:
cosinus(x) + i sinus(x) = e^(ix)
Exemple #1: mettre z = (-5 + 12i) à la forme exponentielle
• z = (-5 + 12i)
• mod(z) = √((-5)² + 12²) = 13
• arg(z) = 2*arctan(12/(-5 + 13)) = 112,61°
• 112,61*Pi/180 = 1,9654 radians
• z = 13(cos(1,9654) + i sin(1,9654))
• comme (cos(x) + i sin(x)) = e^(ix) (formule d'EULER)
• la forme exponentielle de z = (-5 + 12i) est:
z = 13e^(i*1,9654)
Exemple #2: mettre z = (1 + i) à la forme exponentielle
• z = (1 + i)
• mod(z) = √(1² + 1²) = √2
• arg(z) = 2*arctan(1/(1 + √2)) = 45°
• 45*Pi/180 = Pi/4 radians
• z = √2(cos(Pi/4) + i sin(Pi/4))
• comme (cos(x) + i sin(x)) = e^(ix) (formule d'EULER)
• la forme exponentielle de z = (1 + i) est:
z = (√2)*e^(i*Pi/4)
Exemple d'application:
• z = (1 + i)
• z³ = ? (avec la forme exponentielle)
• ----------------------------------------
• z = (1 + i) = (√2)*e^(i*(Pi/4))
• z³ = [(√2)*e^(i*(Pi/4))]³
• z³ = (√2)³*[e^(i*(Pi/4))]³
• z³ = 2√2*[e^(i*(Pi/4)*3)
• z³ = 2√2*e^(i*(3Pi/4))
• z³ = 2√2(cos(3Pi/4) + i sin(3Pi/4)
• z³ = (-2 + 2i)
• z = (1 + i)
• z³ = ? (avec la forme algébrique)
• ----------------------------------------
• z³ = (1 + i)³ = (1 + i)(1 + i)(1 + i)
• z³ = [(1 + i)(1 + i)](1 + i)
• z³ = [1 + i + i + i²](1 + i)
• z³ = [1 + 2i - 1](1 + i)
• z³ = 2i(1 + i)
• z³ = 2i + 2i²
• z³ = 2i - 2
• z³ = (-2 + 2i)
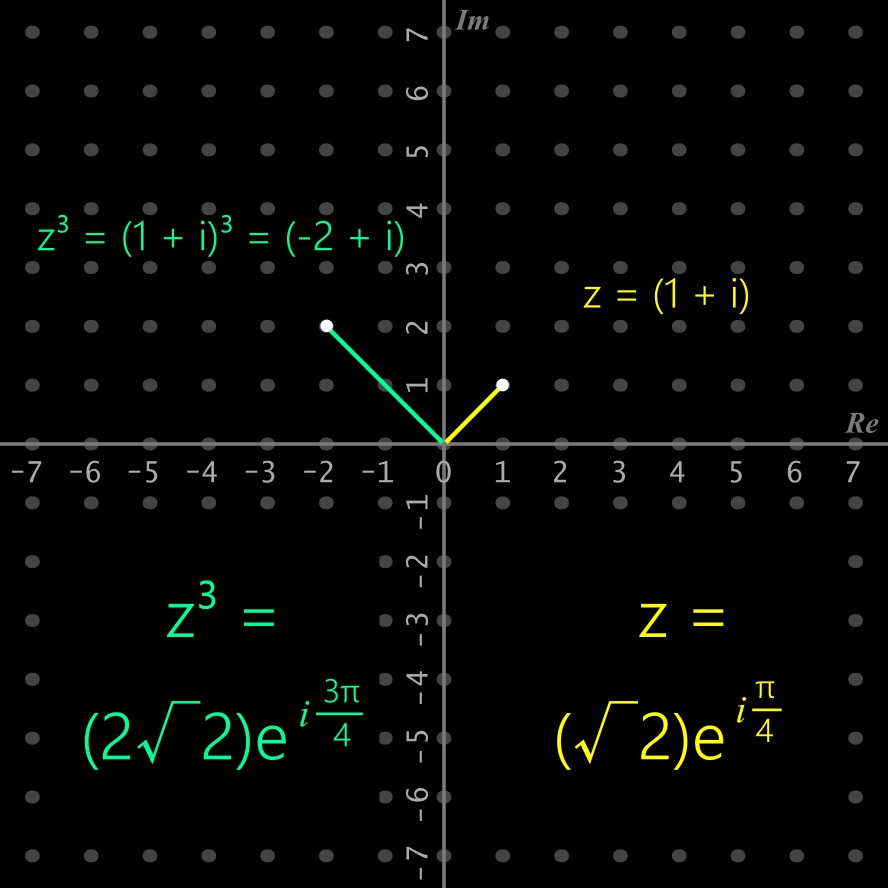
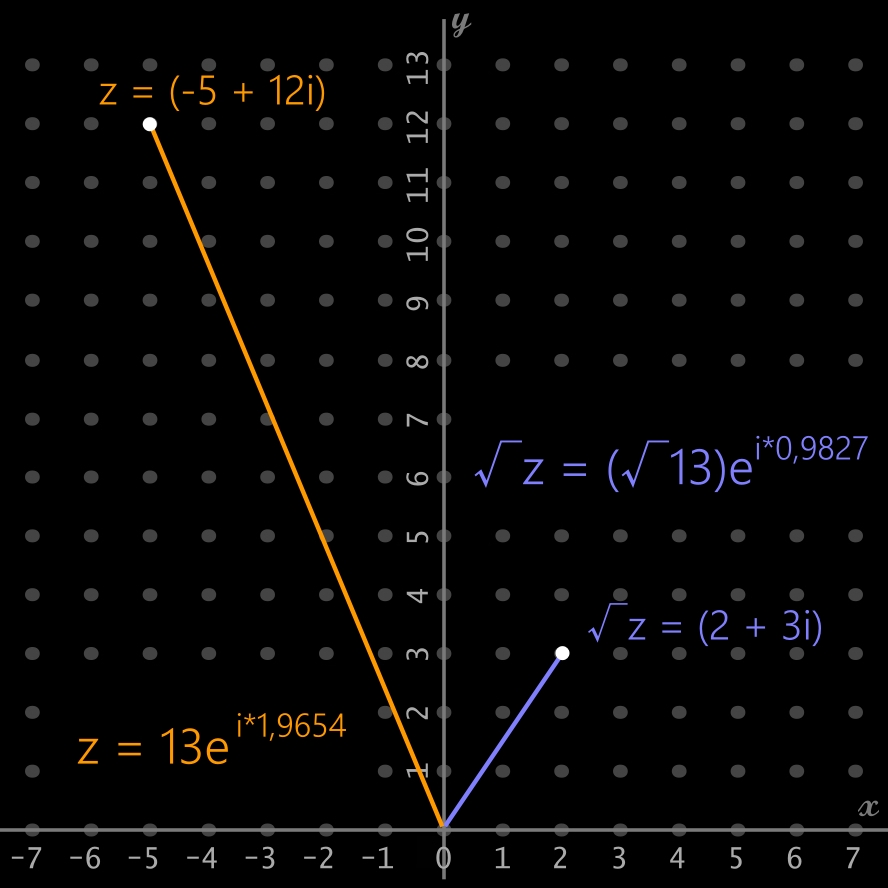
Autre exemple d'application:
• z = (-5 + 12i)
• √z = ? (avec la forme exponentielle)
• z = (-5 + 12i) = 13e^(i*1,9654)
• √z = √[13e^(i*1,9654)]
• √z = (√13)*√(e^(i*1,9654))
• rappel (propriété): √(a^n) = a^(n/2)
• √z = (√13)*e^((i*1,9654)/2)
• √z = (√13)*e^(i*0,9827)
• √z = (√13)(cos(0,9827) + i sin(0,9827))
• √z = (2 + 3i) et (-2 - 3i)
D É M O N S T R A T I O N
Quels sont les liens entre la fonction exponentielle et les fonctions sinus et cosinus ?
Note: cette démonstration fait appel à la série de TAYLOR (mathématicien Britannique, 1685-1731).
La "série de TAYLOR" d'une fonction est une extension de l'approximation polynomiale d'une fonction donnée.
Un exemple d'une fonction "transformée" en série de TAYLOR est disponible (document PDF) en cliquant sur le bouton voir ci-dessous.

Un exemple d'une fonction "transformée" en série de TAYLOR est disponible (document PDF) en cliquant sur le bouton voir ci-dessous.
1. La fonction f(x) = sin(x) peut s'écrire sous la forme de polynomes:
• sin(x) = x - x^3/3! + x^5/5! + x^7/7! + x^9/9! + ...
• ou encore:
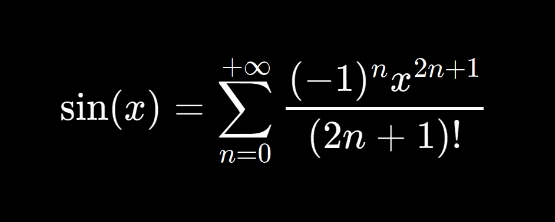
2. La fonction f(x) = cos(x) peut également s'écrire sous la forme de polynomes:
• cos(x) = 1 - x^2/2! + x^4/4! + x^6/6! + x^8/8! + ...
• ou encore:
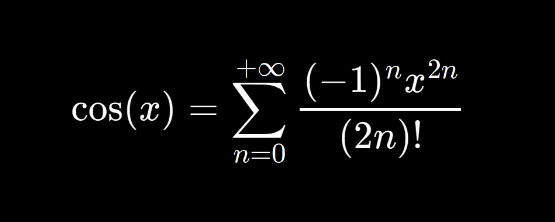
3. Et la fonction exponentielle f(x) = epx(x) peut, elle aussi, s'écrire sous la forme de polynomes:
• epx(x) = 1 + x + x^2/2! + x^3/3! + x^4/4! + x^5/5! + ...
• ou encore:
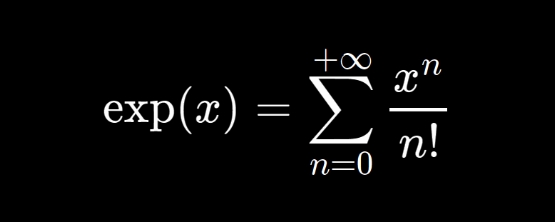
4. Les puissances de i pour faire le lien entre les fonctions sinus et cosinus et la fonction exponentielle:
• (0 + i)^2 = (0 + i)(0 + i) = i^2 ............ = -1
• (0 + i)^3 = (0 + i)(0 + i)^2 = (0 + i)(0 - 1) = -i
• (0 + i)^4 = (0 + i)(0 + i)^3 = (0 + i)(0 - i) = +1
• (0 + i)^5 = (0 + i)(0 + i)^4 = (0 + i)(0 + 1) = +i
• (0 + i)^6 = (0 + i)(0 + i)^5 = (0 + i)(0 + i) = -1
• (0 + i)^7 = (0 + i)(0 + i)^6 = (0 + i)(0 - 1) = -i
• (0 + i)^8 = (0 + i)(0 + i)^7 = (0 + i)(0 - i) = +1
• (0 + i)^9 = (0 + i)(0 + i)^8 = (0 + i)(0 + 1) = +i
• ...
• etc.

|

|

|

