Pourquoi le rapport sinus sur cosinus donne la tangente? Explications ci-dessous ...










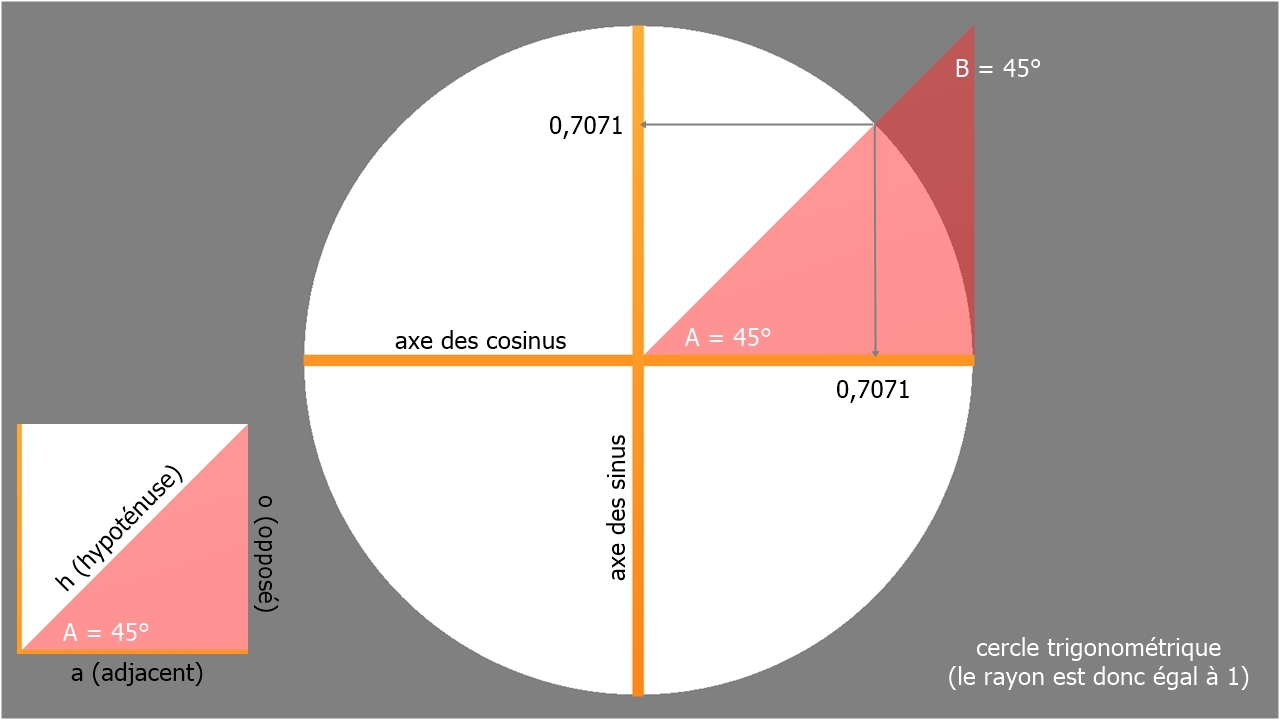
figure 1




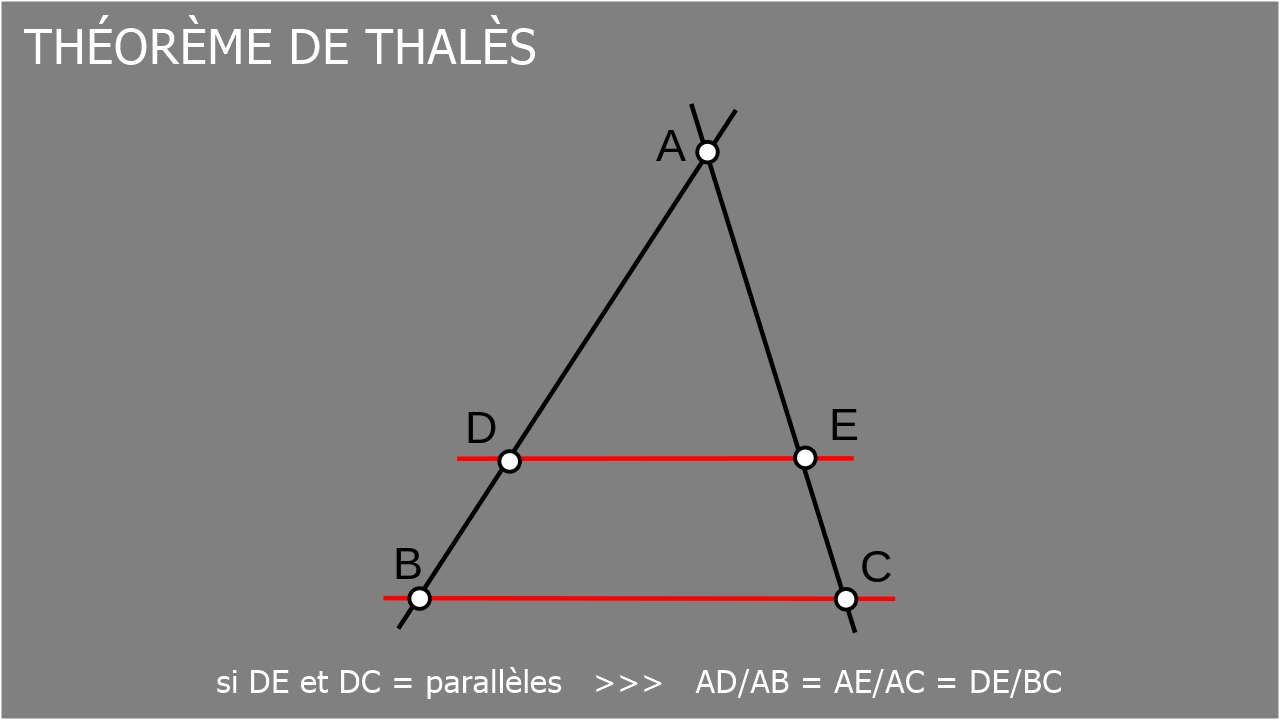
figure 2




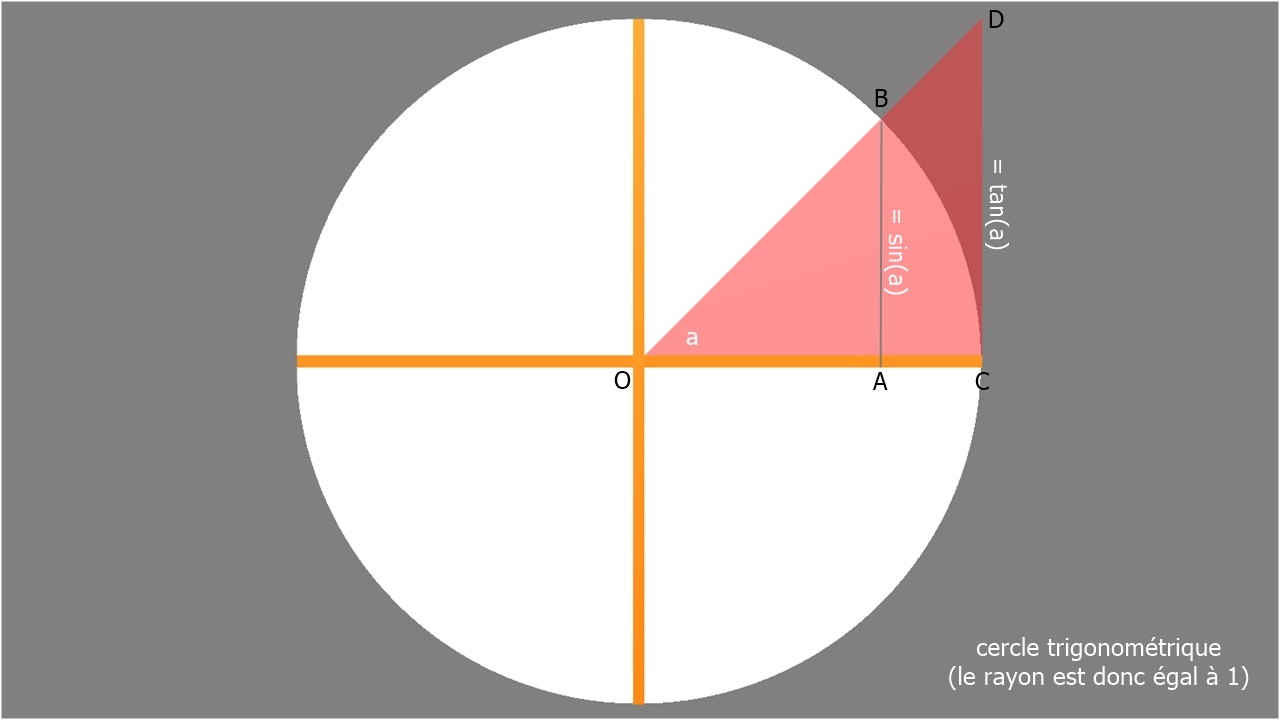
figure 3





==================================================
1. TANGENTE = SINUS / COSINUS (CONSTATATION)
==================================================


• "casse-toi!" ou "cah soh toa" ... pour se rappeler les bases (figure 1):

  cah comme cosinus = rapport entre le côté adjacent et l'hypothénuse: cos(A)=a/h

  soh comme sinus = rapport entre le côté opposé et l'hypothénuse: sin(A)=o/h

  toa comme tangente = rapport entre le côté opposé et adjacent: tan(A)=o/a

• vérifions que TANGENTE = SINUS / COSINUS:

  sin(A) / cos(A) = o/h / a/h = o/h x h/a = (en simplifiant) o/a

  or o/a est bien le rapport de la tangente (tan(A)=o/a)

  on obtient donc bien: TANGENTE = SINUS / COSINUS

• exemple chiffré (avec un angle de 45° comme sur la figure 1):

  sin(45) = 0,7071

  cos(45) = 0,7071

  tan(45) = sin(45) / cos(45) = 0,7071 / 0,7071 = 1

  effectivement, la tangente de 45 est bien égale à 1

  note: sinus = cosinus car il s'agit d'un triangle isocèle

• autre exemple (avec un angle de 22°):

  sin(22) = 0,37460

  cos(22) = 0,92718

  tan(22) = sin(22) / cos(22) = 0,37460 / 0,92718 = 0,40402

  effectivement, la tangente de 22 est bien égale à 0,40402



===================================================
2. TANGENTE = SINUS / COSINUS (DÉMONSTRATION)
===================================================


• rappel du théorème de THALÈS (figure 2):

  dans un triangle ABC et deux points D et E des droites AB et AC ...

  de sorte que la droite DE soit parallèle à la droite BC ...

  le théorème de THALÈS dit alors que:

  ---------------------
  AD/AB = AE/AC = DE/BC
  ---------------------

• appliquons le théorème de THALÈS au triangle OCD (figure 3)

• on sait que OA/OC = OB/OD = AB/CD, procédons alors en 4 étapes

• 1) comme OC est égal à l'hypoténuse OB on peut écrire:

  OA/OC = cos(a)

• 2) comme AB est égal au sinus de l'angle a on peut écrire:

  AB/CD = sin(a)/CD

• 3) comme OA/OC = AB/CD on peut aussi l'écrire ainsi:

  cos(a) = sin(a)/CD donc CD = sin(a)/cos(a)

• 4) et enfin comme CD est égal à la tangente de l'angle a on peut écrire:

  tan(a)= sin(a)/cos(a)

• la démonstration est faite!