

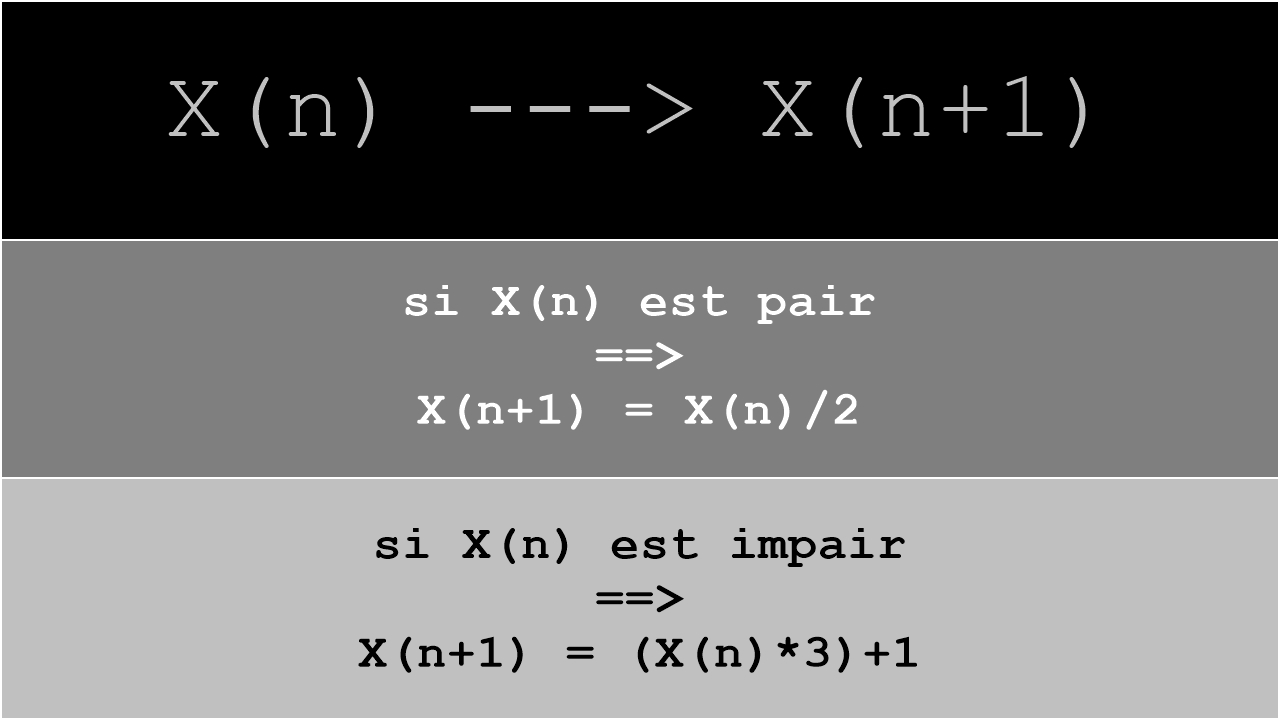
01
suite de Syracuse
-----------------------
La suite de Syracuse une suite d'entiers naturels qui débute par un nombre entier plus grand que zéro:
(voir également l'image 01, ci-dessus)
• si ce nombre est pair, on le divise par 2
• si ce nombre est impair, on le multiplie par 3 et on ajoute 1
Exemple en partant du nombre entier naturel 7:
<> 7 est impair donc le nombre suivant sera (7*3)+1 = 22
<> 22 est pair donc le nombre suivant sera 22/2 = 11
<> 11 est impair donc le nombre suivant sera (11*3)+1 = 34
<> 34 est pair donc le nombre suivant sera 34/2 = 17
<> etc ...
<> on obtiendra donc la suite de Syracuse suivante:
7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, 4, 2, 1 ...
Autre exemple en partant du nombre entier naturel 33:
<> 33 est impair donc le nombre suivant sera (33*3)+1 = 100
<> 100 est pair donc le nombre suivant sera 100/2 = 50
<> 50 est pair donc le nombre suivant sera 50/2 = 25
<> 25 est impair donc le nombre suivant sera (25*3)+1 = 76
<> 76 est pair donc le nombre suivant sera 76/2 = 38
<> etc ...
<> on obtiendra donc la suite de Syracuse suivante:
33, 100, 50, 25, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13,
40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, 4, 2, 1 ...
Dernier exemple en partant du nombre entier naturel 79:
<> on obtiendra la suite de Syracuse suivante:
79, 238, 119, 358, 179, 538 269, 808, 404, 202, 101, 304, 152, 76, 38, 19,
58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1,
4, 2, 1, 4, 2, 1 ...
Or, que constate-t-on?
QUELQUE SOIT LE NOMBRE DE DÉPART, LA SUITE DE SYRACUSE SEMBLE SE TERMINER TOUJOURS PAR LA SÉQUENCE INDÉFINIE << 4, 2, 1, ... >>.
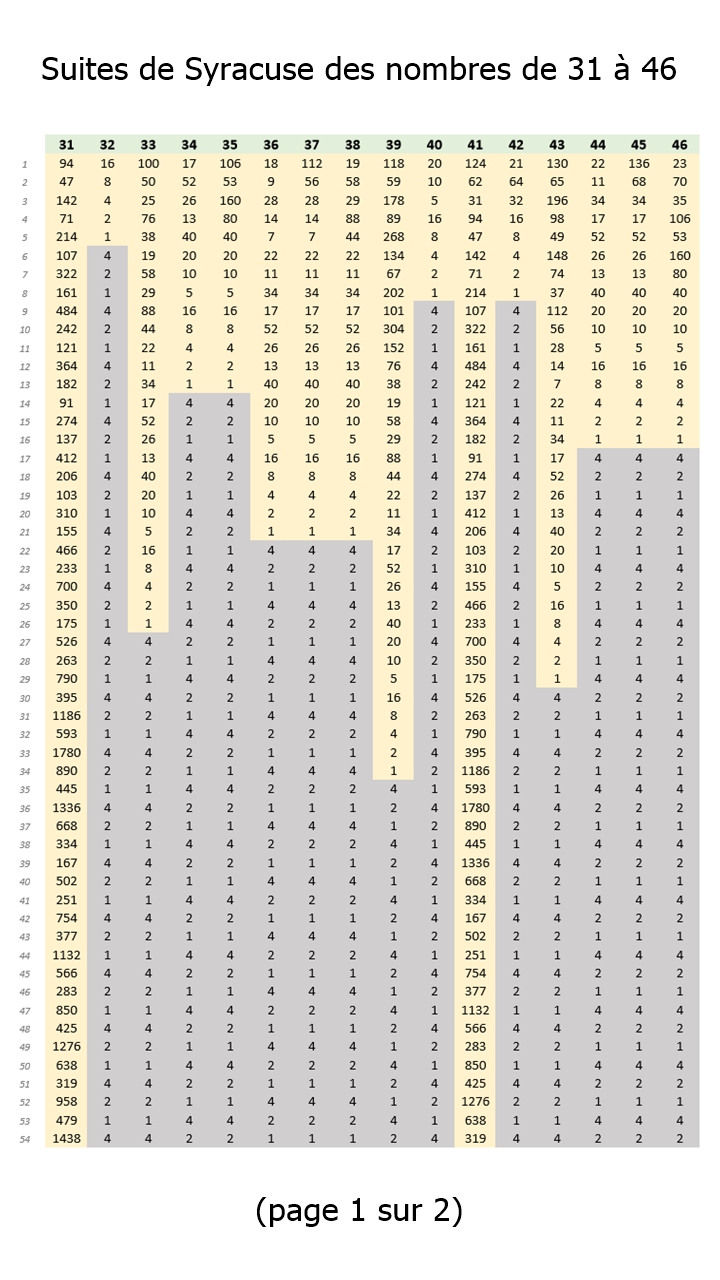
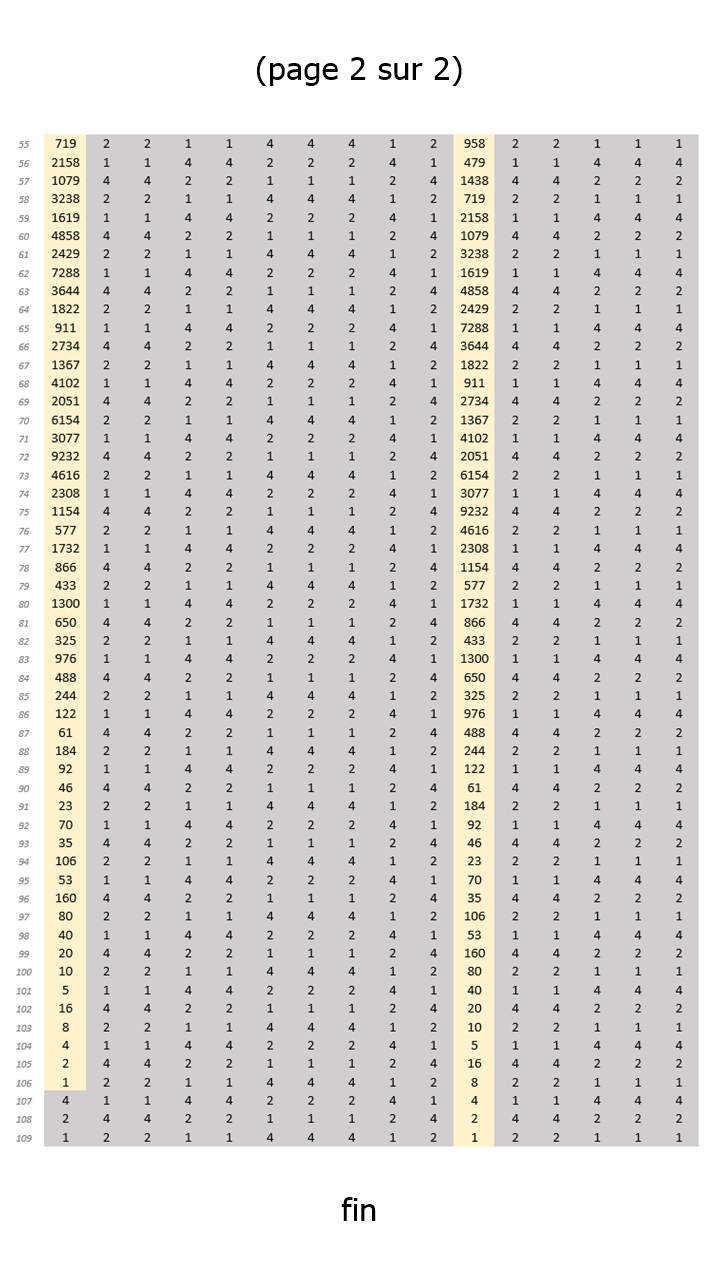
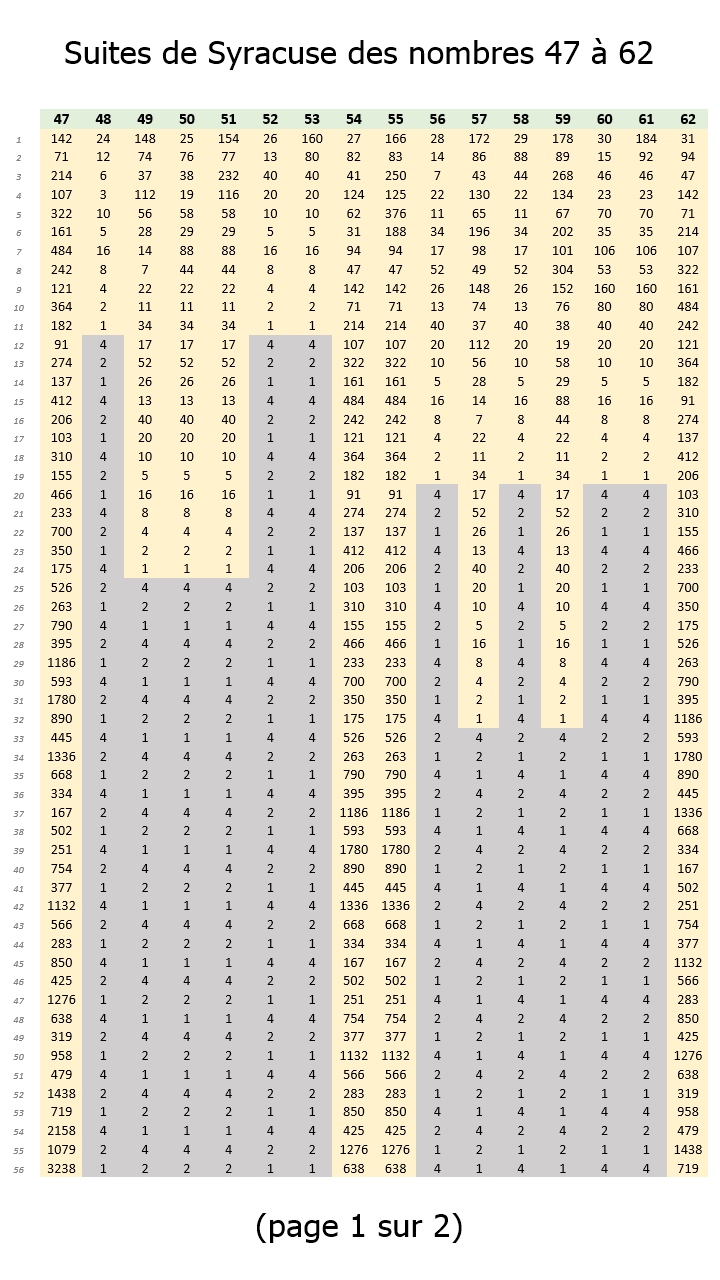
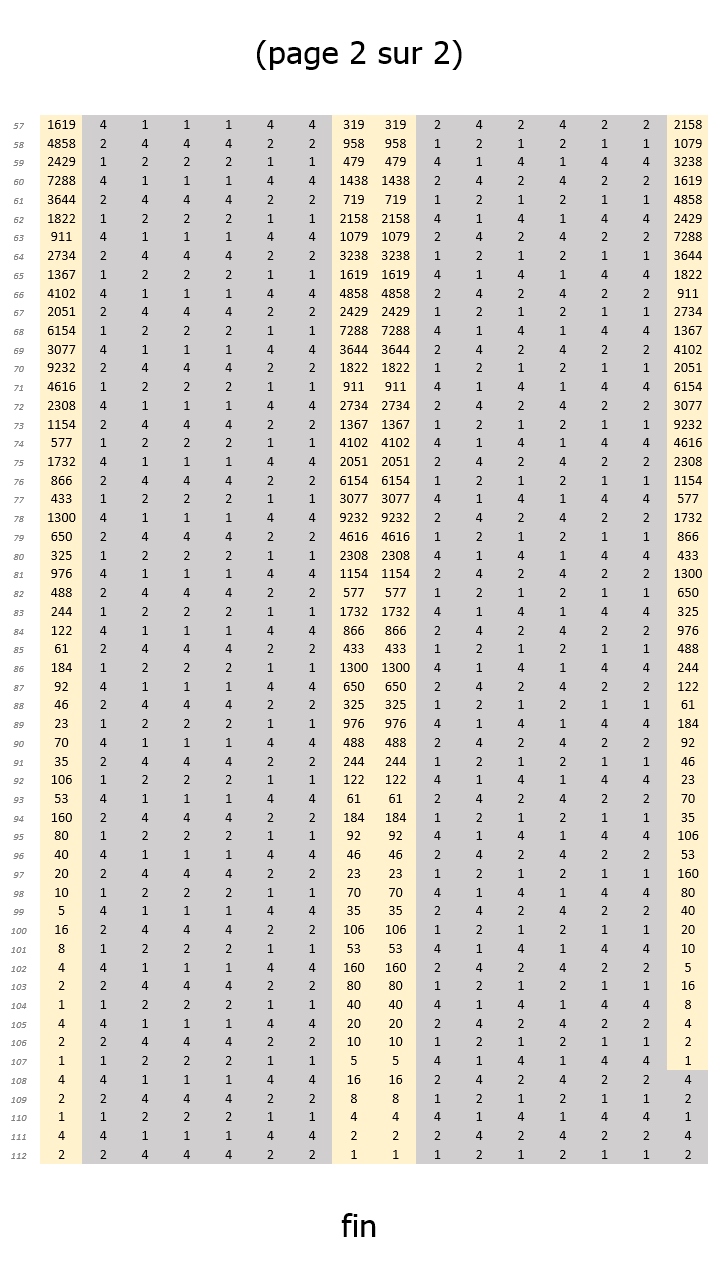
Les images 02, 03, 04 et 05 ci-dessous montrent, à titre d'exemple, les suites de Syracuse pour les nombres entiers naturels entre 31 et 62 (calculées avec le tableur EXCEL de Microsoft). Et de constater que toutes se terminent par la séquence << 4, 2, 1, ... >>.
conjecture de Syracuse
----------------------------
Comment démontrer que les suites de Syracuse se termineraient toujours par la séquence << 4, 2, 1, ... >>?
Réponse: on ne sait pas le démontrer!
Mais alors, comment prouver que cette propriété est vérifiée pour toute série commençant par un nombre entier plus grand que zéro?
Réponse: PAR LE CONSTAT!
Note: ne pas pouvoir démontrer mathématiquement une caractéristique alors qu'elle semble très plausible, car vérifiée sur un grand nombre d’exemples, est ce qu'on appelle une CONJECTURE (si cette caractéristique était démontrable on pourrait en tirer un THÉORÈME).
Cette conjecture défie depuis de nombreuses années les mathématiciens.
Paul ERDOS (mathématicien hongrois, 1913-1996) a dit à propos de la conjecture de Syracuse: "les mathématiques ne sont pas encore prêtes pour de tels problèmes".
table des suites de Syracuse pour les nombres de 31 à 62
--------------------------------------------------------------
Information: afin de réaliser les tables (images ci-dessous) des suites de Syracuse, j'ai utilisé la formule (simple) EXCEL qui est:
/\/\/\/\
/\/\/\
/\/\
/\
•
