


image 01
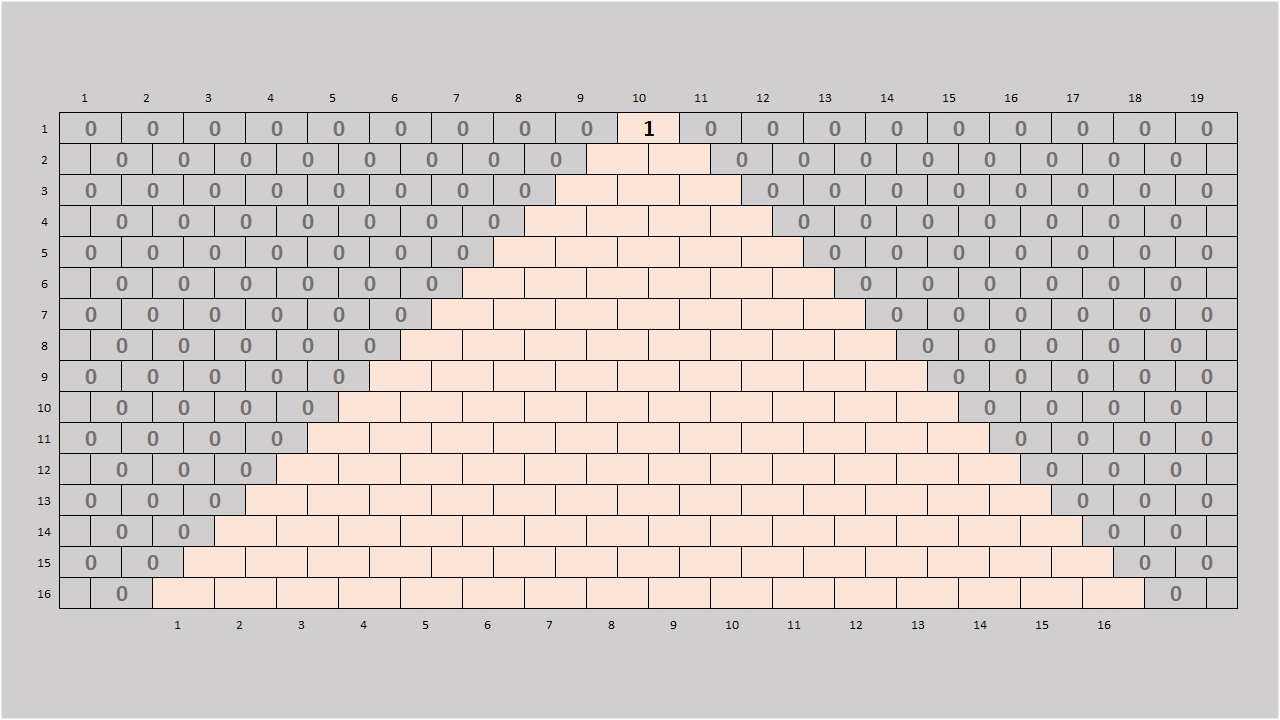
image 02
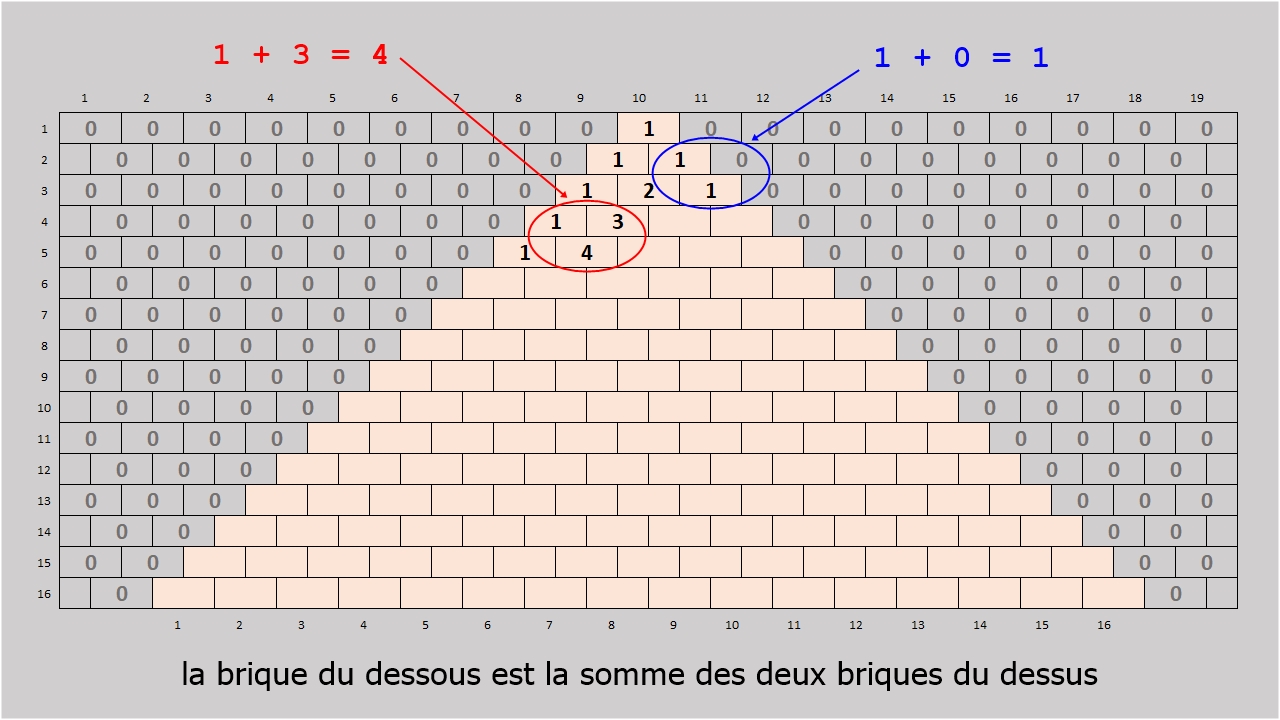
image 03

image 04
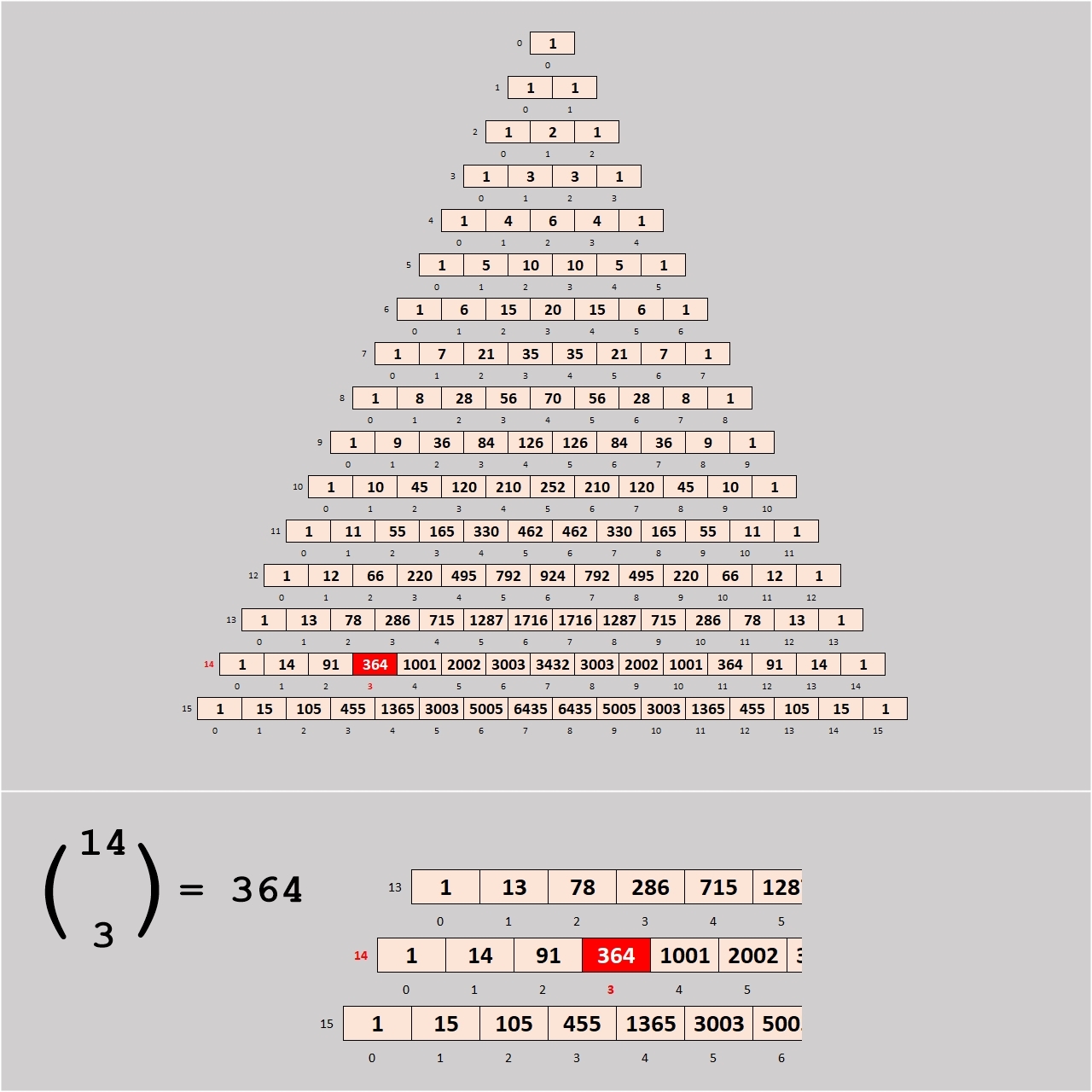
image 05
I N T R O D U C T I O N
-----------------------------
En mathématiques, le triangle de PASCAL est une présentation, dans un triangle, des coefficients binômiaux.
Pour bien comprendre ce qui précède nous allons procéder en 5 étapes (5 sections):
• "fabrication" du triangle,
• rappel sur les combinaisons,
• le triangle de PASCAL et les combinaisons,
• le triangle de PASCAL et les identités remarquables,
• coefficients binômiaux.
"fabrication" du triangle
-------------------------------
C'est très simple ...
Il faut d'abord imaginer un mur de briques bien posées en quinconce les unes sur les autres et à qui on attribue la valeur 0 (zéro) pour chacune d'entre elles: voir l'image 01 (ci-dessus). Note: des briques qui prennent des valeurs, c'est possible ... en mathématique :-))
Il faut ensuite considérer une section triangulaire de ce mur avec 1 brique au sommet et 16 briques à la base (ou davantage car le triangle peut être plus grand). On attribue la valeur 1 à la brique du sommet du triangle: voir l'image 02 (ci-dessus).
Chaque brique du triangle prendra une valeur égale à la somme des deux briques placées juste au-dessus: voir l'image 03 (ci-dessus).
En attribuant une valeur à chaque brique du triangle (rappel: chaque brique est égale à la somme des deux briques placées juste au-dessus) on aura constitué le TRIANGLE DE PASCAL: voir l'image 04 (ci-dessus).
rappel sur les combinaisons
---------------------------------

Prenons le jeu du LOTO comme exemple classique: combien y a-t-il de combinaisons à 6 chiffres dans une grille qui en comporte 49 (de 1 à 49)?



Notes à propos des factorielles (révisions):
• La factorielle de n est le produit de tous les nombres entiers de 1 à n.
• Une factorielle est notée par un point d'exclamation.
• Exemple: 6! = 1 x 2 x 3 x 4 x 5 x 6 = 720.
• Attention: 0! = 1 et non pas 0 (*)
(*) Explication: 6!=720, 5!=120, 4!=24, 3!=6, 2!=2, 1!=1, 0!=1 et si on considère la suite << 720, 120, 24, 6, 2, 1, 1 >> la factorielle de 0 est égale à 1 car la progression est une division par 6 (entre 720 et 120), puis par 5 (entre 120 et 24), puis par 4 (entre 24 et 6), puis par 3 (entre 6 et 2), puis par 2 (entre 2 et 1) et donc par 1 (entre 1 et 1). Donc la factorielle de 0 est égale à 1, tout comme la factorielle de 1.

Prenons un autre exemple: combien y a-t-il de combinaisons avec 2 cartes dans un jeu de 52 cartes à jouer (main de 2 cartes distribuées à chaque joueur dans le cas du poker texas hold'em)?
Résultat:

Dernier exemple: combien y a-t-il de tiercés (combinaisons de 3 chevaux) dans une course qui comprend 14 chevaux en tout?
Résultat:
le triangle de PASCAL et les combinaisons
-----------------------------------------------
Nous venons de calculer le nombre de combinaisons de 3 (k) parmi 14 (n) en appliquant la formule:
Mais sans la formule, nous pouvons trouver le résultat dans le triangle de PASCAL.
Pour cela il suffit de lire la valeur de la "brique" du triangle de PASCAL (voir l'image 05, ci-dessus) située à la 14e couche (n) à la position 3 (k) pour lire directement le résultat 364 (vous noterez que les couches et positions sont comptées à partir de 0 et non à partir de 1).
De la même façon nous pouvons trouver directement le résultat, par exemple, du nombre de combinaisons de 8 parmi 13 qui est 1287, ou de 11 parmi 15 qui est 1365, etc.
Le triangle de PASCAL révèle 4 petits "secrets" très intéressants:
1) on constate que quand k = n, le résultat est toujours 1 (exemples ci-dessous: le nombre de combinaisons de 14 parmi 14 est 1, et celui de 15 parmi 15 est 1),
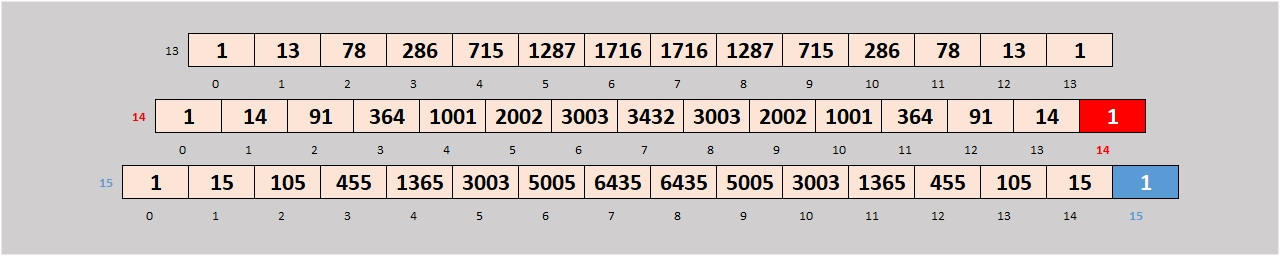
2) on constate que quand k = 1, le résultat est toujours n (exemples ci-dessous: le nombre de combinaisons de 1 parmi 13 est 13, et celui de 1 parmi 14 est 14),
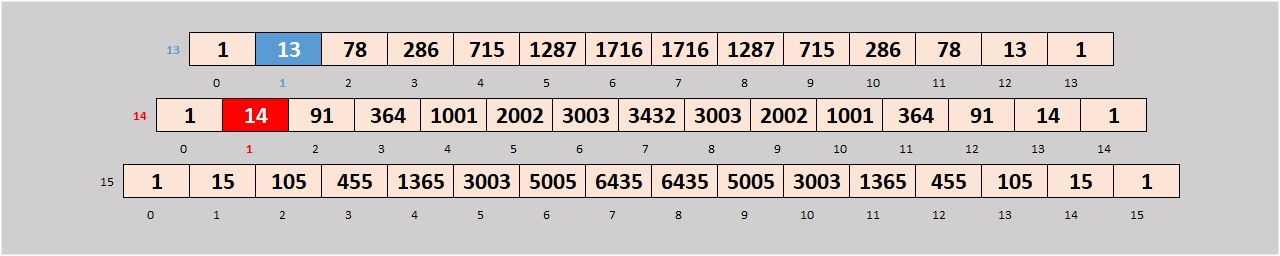
3) on constate que la combinaison de k parmi n est égale à la combinaison de (n-k) parmi n (exemples ci-dessous: le nombre de combinaisons de 3 parmi 14 [364] est équivalent au nombre de combinaisons de 11 (14-3) parmi 14 [364], de même celui de 6 parmi 15 [5005] est équivalent à 9 (15-6) parmi 15 [5005]),
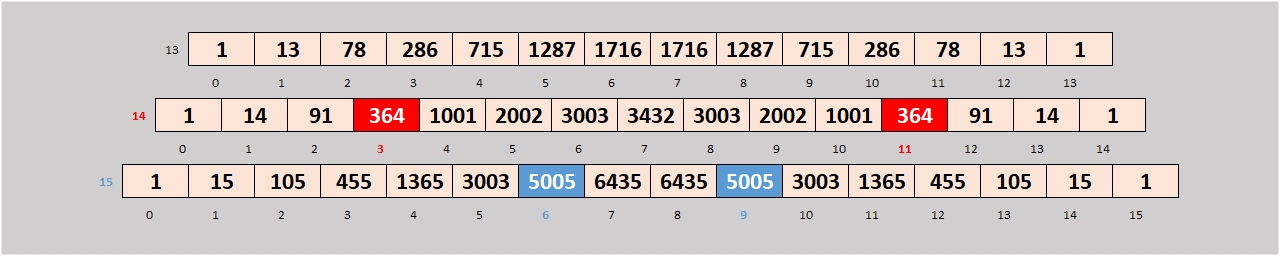
4) on constate enfin que le nombre de combinaisons de k parmi n est égal à celui de n-1 parmi k-1 + celui de n-1 parmi k (exemple ci-dessous: le nombre de combinaisons de 3 (k) parmi 14 (n) [364] est la somme du nombre des combinaisons de 2 (k-1) parmi 13 (n-1) [78] et de 3 (k) parmi 13 (n-1) [286]),
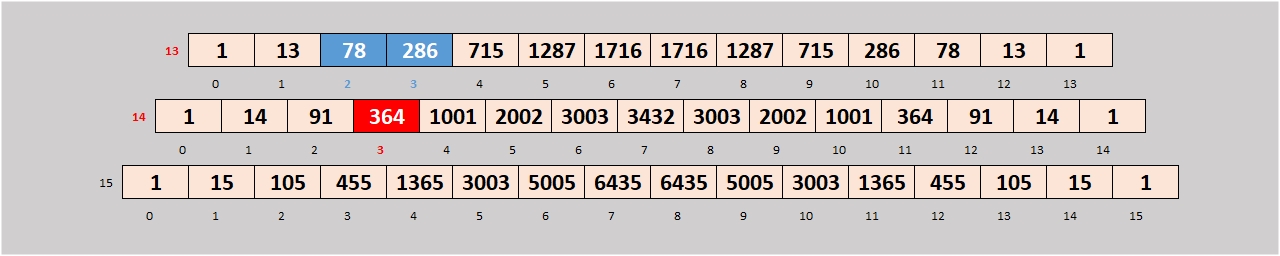
... et on peut donc résumer ainsi ces 4 propriétés:
1) si k = n alors C[k parmi n] = 1
2) si k = 1 alors C[1 parmi n] = n
3) C[k parmi n] = C[(n-k) parmi n]
4) C[k parmi n] = C[(k-1) parmi (n-1)] + C[k parmi (n-1)]
(comme l'addition est commutative, on peut aussi écrire un "4b")
4b) C[k parmi n] = C[k parmi (n-1)] + C[(k-1) parmi (n-1)]
On constate également sur le triangle de PASCAL que le nombre de combinaisons est toujours égal à 1 aussitôt que k = 0. On peut ainsi ajouter une cinquième propriété:
5) si k = 0 alors C[0 parmi n] = 1
LA SECTION SUIVANTE VA DÉMONTRER COMBIEN LE TRIANGLE DE PASCAL, LES COMBINAISONS ET LES IDENTITÉS REMARQUABLES SONT ÉTROITEMENT LIÉS.
le triangle de PASCAL et les identités remarquables
---------------------------------------------------------
Les trois identités remarquables (*) du 2e degré sont (rappel):
• (a+b)2 = (a+b)(a+b) = a2+ab+ba+b2 = a2+2ab+b2
• (a-b)2 = (a-b)(a-b) = a2-ab-ba+b2 = a2-2ab+b2
• (a+b)(a-b) = a2-ab+ba-b2 = a2-ab+ab-b2 = a2-b2
(*) Note: les identités remarquables sont des expressions algébriques (également appelées formules) qui servent de modèle aux exercices de développement et de factorisation.
Voici l'exemple d'une identité du 3e degré et une autre du 4e degré:
• (a+b)3 = a3 + 3a2b + 3ab2 + b3
• (a+b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
Ci-dessous, le lien entre le triangle de PASCAL et les identités remarquables:
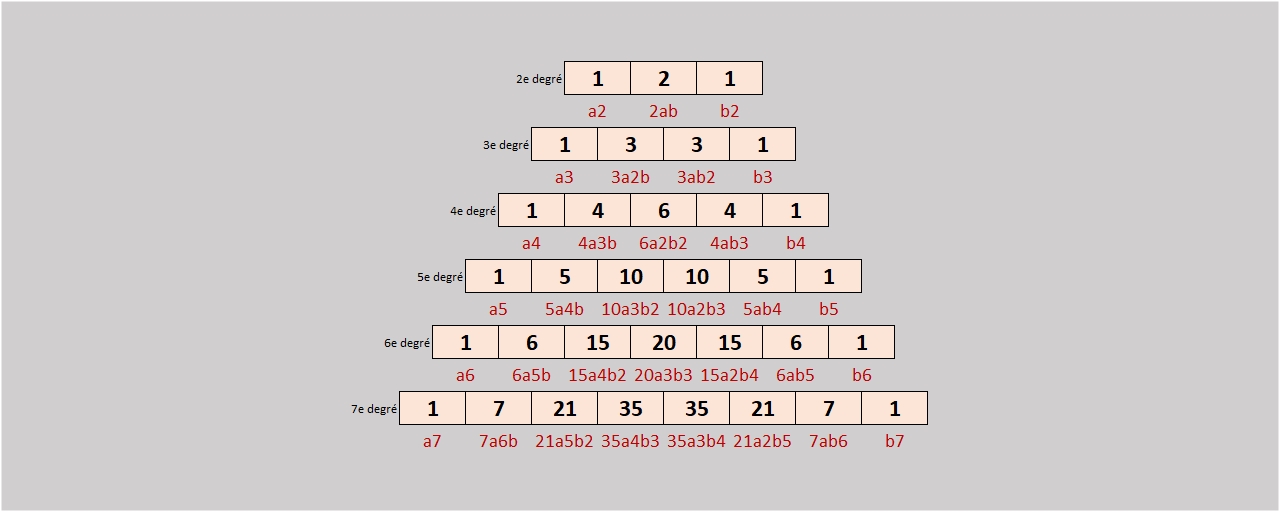
Le triangle de PASCAL fournit les COEFFICIENTS de chaque terme d'une identité.
Dans le cas de l'exemple d'une identité remarquable au 5e degré, le triangle de PASCAL fournit les coefficients 1, 5, 10, 10, 5 et 1 (voir l'image ci-dessus) qui correspondent au développement de l'identité:
(a+b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5
avec le coefficient 1 .... pour a5 ....... (soit 1 fois a5),
avec le coefficient 5 .... pour 5a4b ..... (soit 5 fois a4b),
avec le coefficient 10 ... pour 10a3b2 ... (soit 10 fois a3b2),
avec le coefficient 10 ... pour 10a2b3 ... (soit 10 fois a2b3),
avec le coefficient 5 .... pour 5ab4 ..... (soit 5 fois ab4)et
avec le coefficient 1 .... pour b5 ....... (soit 1 fois b5).
MAIS IL Y A ENCORE D'AUTRES LIENS ENTRE LES IDENTITÉS REMARQUABLES ET LE TRIANGLE DE PASCAL ET OÙ INTERVIENNENT LES COMBINAISONS.
Il existe une formule pour développer une identité remarquable quelque soit son degré.
Voici cette formule:
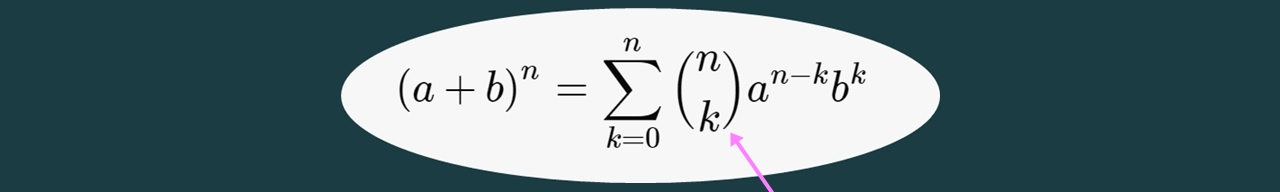
On constate qu'intervient un nombre de combinaisons de k parmi n.
Appliquons cette formule pour une identité remarquable de degré 5.
Développons pour chaque itération de k à n (au départ k=0 et n=5):
pour k = 0, le premier terme est:
• (nbe de combinaisons de 0 parmi 5) x (a puissance (5-0)) x (b puissance 0) = a5
pour k = 1, le deuxième terme est:
• (nbe de combinaisons de 1 parmi 5) x (a puissance (5-1)) x (b puissance 1) = 5a4b
pour k = 2, le troisième terme est:
• (nbe de combinaisons de 2 parmi 5) x (a puissance (5-2)) x (b puissance 2) = 10a3b2
pour k = 3, le quatrième terme est:
• (nbe de combinaisons de 3 parmi 5) x (a puissance (5-3)) x (b puissance 3) = 10a2b3
pour k = 4, le cinquième terme est:
• (nbe de combinaisons de 4 parmi 5) x (a puissance (5-4)) x (b puissance 4) = 5ab4
pour k = 5, le cinquième et dernier terme est:
• (nbe de combinaisons de 5 parmi 5) x (a puissance (5-5)) x (b puissance 5) = b5
Ce qui fait bien: (a+b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5
On notera l'utilisation du triangle de PASCAL pour le calcul des combinaisons et/ou pour l'utilisation des propriétés qui en découlent.
coefficients binômiaux
----------------------------
La formule utilisée dans la section précédente pour développer une identité remarquable quelque soit son degré porte le nom de FORMULE DU BINÔME (définie par Isaac NEWTON).
Cette formule fait intervenir les combinaisons pour définir les coefficients du binôme, ce sont les COEFFICIENTS BINÔMIAUX.
Ainsi, les coefficients du binôme (*) (a+b)5 sont 1, 5, 10, 10, 5 et 1.
(*) Notes:
- un polynôme désigne une expression algébrique composée de
plusieurs termes (appelés monômes) séparés par le signe + ou -
- un monôme désigne une expression algébrique ne comportant que
des multiplications comme par exemple -7/2a2bc
- un binôme désigne une expression algébrique comportant 2
monômes comme par exemple (a-b)5
/\/\/\/\
/\/\/\
/\/\
/\
•
