
pourquoi 1,618...
est-il appelé
nombre d'or?
est-il appelé
nombre d'or?

Quelle est la propriété de 1,618...?
------------------------------------------
Le nombre 1,618 (et plus précisemmet 1,618033989... etc.) est le rapport qu'il faut appliquer entre la longueur et la largeur d'un rectangle pour obtenir un rectangle harmonieux.
Un rectangle harmonieux (appelé le plus souvent « rectangle d'or »), imaginé par les grecs anciens, a la propriété que quand un carré lui est enlevé, il reste un rectangle certes plus petit mais de la même forme en terme de proportions que le rectangle initial.
Pour bien comprendre, suivre les 8 étapes (en images commentées) juste ci-dessous.

1) Soit, par exemple, un rectangle de 21,84 sur 13,50 centimètres (harmonieux
car 13,5 x 1,618 = 21,84),

2) puis découpons-le en formant un carré à gauche et rectangle à droite,

3) et superposons le rectangle (issu du découpage) sur le rectangle initial,

4) on peut alors vérifier qu'en étirant le rectangle sur l'axe de la diagonale
du rectangle initial,

5) il est ...

6) pafaitement ...

7) proportionnel ...

8) au rectangle initial.
On pourrait répéter indéfiniment cette séquence en redécoupant de la même façon un nouveau rectangle dans le rectangle issu du découpage, et recommencer.
D'où vient 1,618...?
Comment a-t-il été caculé?
--------------------------------
Il faut regarder l'image ci-dessous:
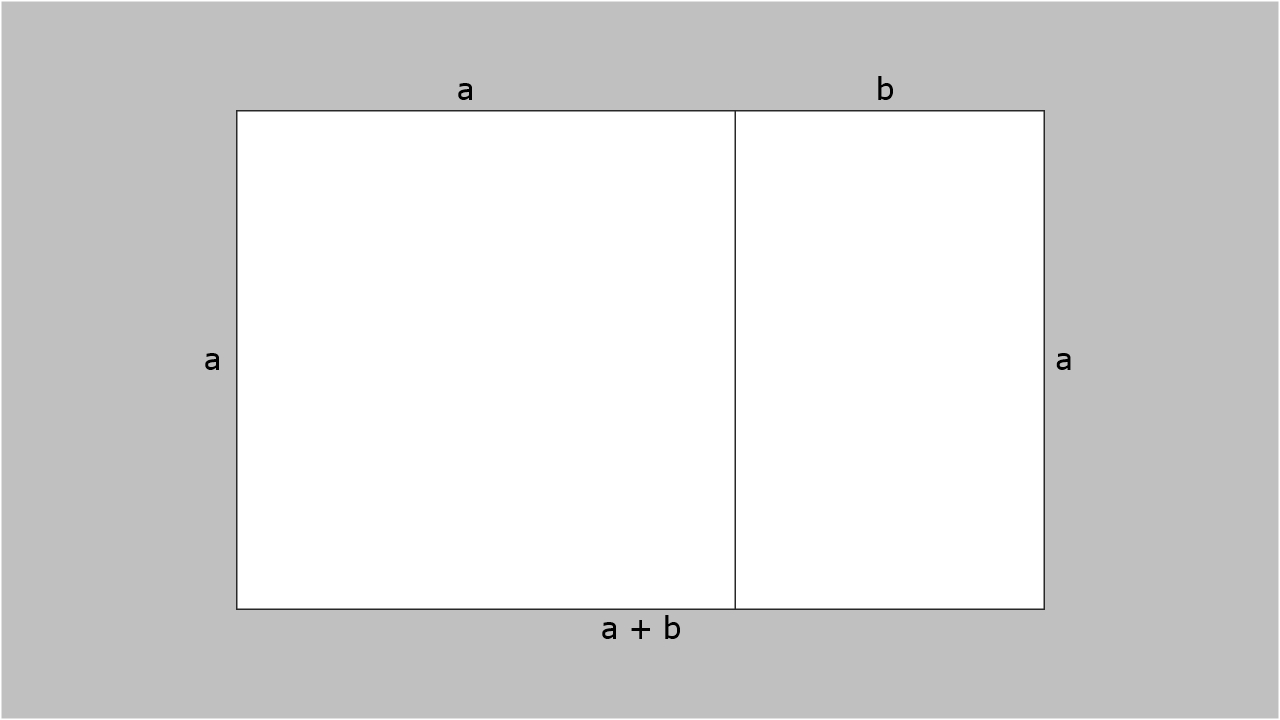
Sur cette image (ci-dessus) on voit:
• le rectangle harmonieux initial dont la longueur est a+b et la largeur a,
• le carré a sur a découpé dans le rectangle initial,
• le rectangle a sur b obtenu après le découpage du carré.
On sait que le rapport de la longueur (a+b) sur la largeur (a) du grand rectangle doit être égal au rapport de la longueur (a) sur la largeur (b) du petit rectangle, et donc on peut écrire:
• (a + b) / a = a / b
• remplaçons a par 1 (comme 1 centimètre ou 1 mètre ou 1 kilomètre, ...)
(note: une autre valeur aurait pu être choisie pour le cacul à la place de 1)
• remplaçons b par x (x étant l'inconnue que nous allons calculer)
(note: à la place de b, a aurait pu être choisie comme étant l'inconnue)
• on obtient: (1 + x) / 1 = 1 / x
• il en découle (mathématiquement): x(1 + x) = 1 x 1
• et donc: x² + x = 1
• et donc x² + x - 1 = 0
• et c'est une équation du 2e degré de type « y = ax² + bx + c » avec:
a = 1
b = 1
c = -1
• calculons le déterminant delta (delta = b² - 4ac):
• delta = b² - 4ac = 1² - 4(1·-1) = 1 - (-4) = 5
• delta étant positif (=5) calculons x = (-b + racine(delta)) / 2a
• x = (-b + racine(delta)) / 2a = (-1 + racine(5)) / 2 = 0.618033989
Reportons le résultat de notre calcul sur l'image précédente pour donner l'image suivante:
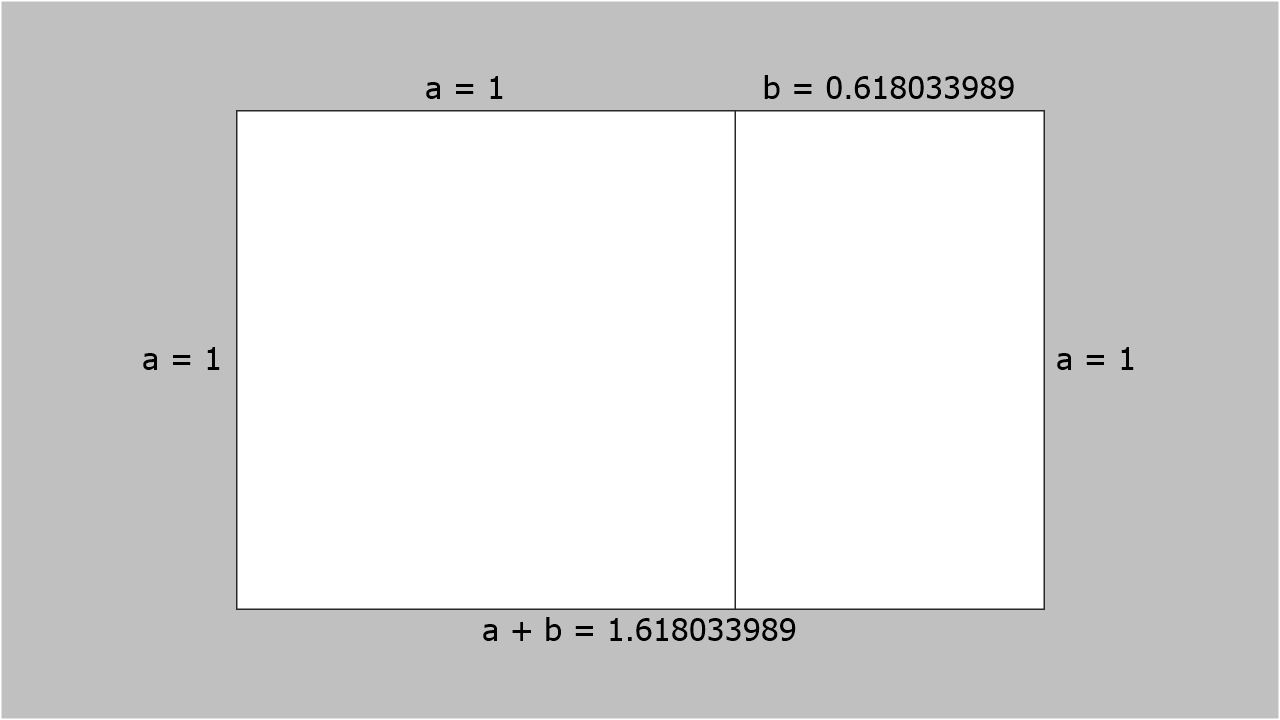
Maintenant que nous connaissons a (=1) et b (=0.618033989), calculons le nombre d'or:
• pour le grand rectangle: nombre d'or = 1,618033989 / 1 = 1,618033989
• pour le petit rectangle: nombre d'or = 1 / 0.618033989 = 1,618033989
Il y aurait encore d'autres choses à dire sur le nombre d'or (cette page aura donc une suite) mais l'essentiel est déjà dit.
à suivre
