
trouver
l'équation
du cercle
dans un
repère orthonormé
l'équation
du cercle
dans un
repère orthonormé

Soit, dans un repère orthonormé (*), un cercle de rayon = 1, tracé au compas, la pointe bien au centre (sur 0).
(*) Note: un repère orthonormé en deux dimensions est un repère dont l'axe (horizontal) des x est perpendiculaire à l'axe (vertical) des y, et dont la taille des graduations est la même pour les deux axes.
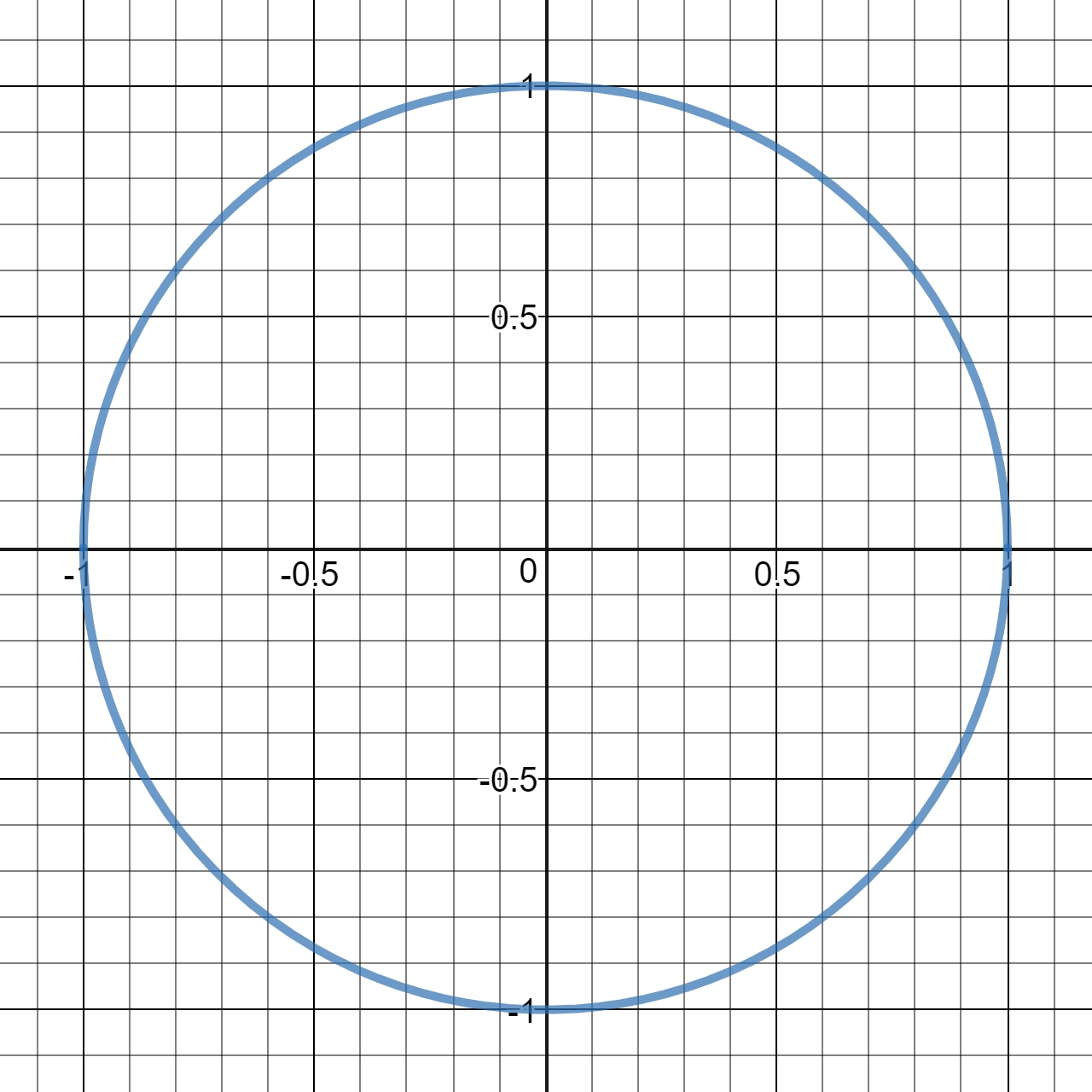
Exemple d'un point du cercle (image ci-dessous) qui a pour valeur x = 0,5 et y = 0,866.
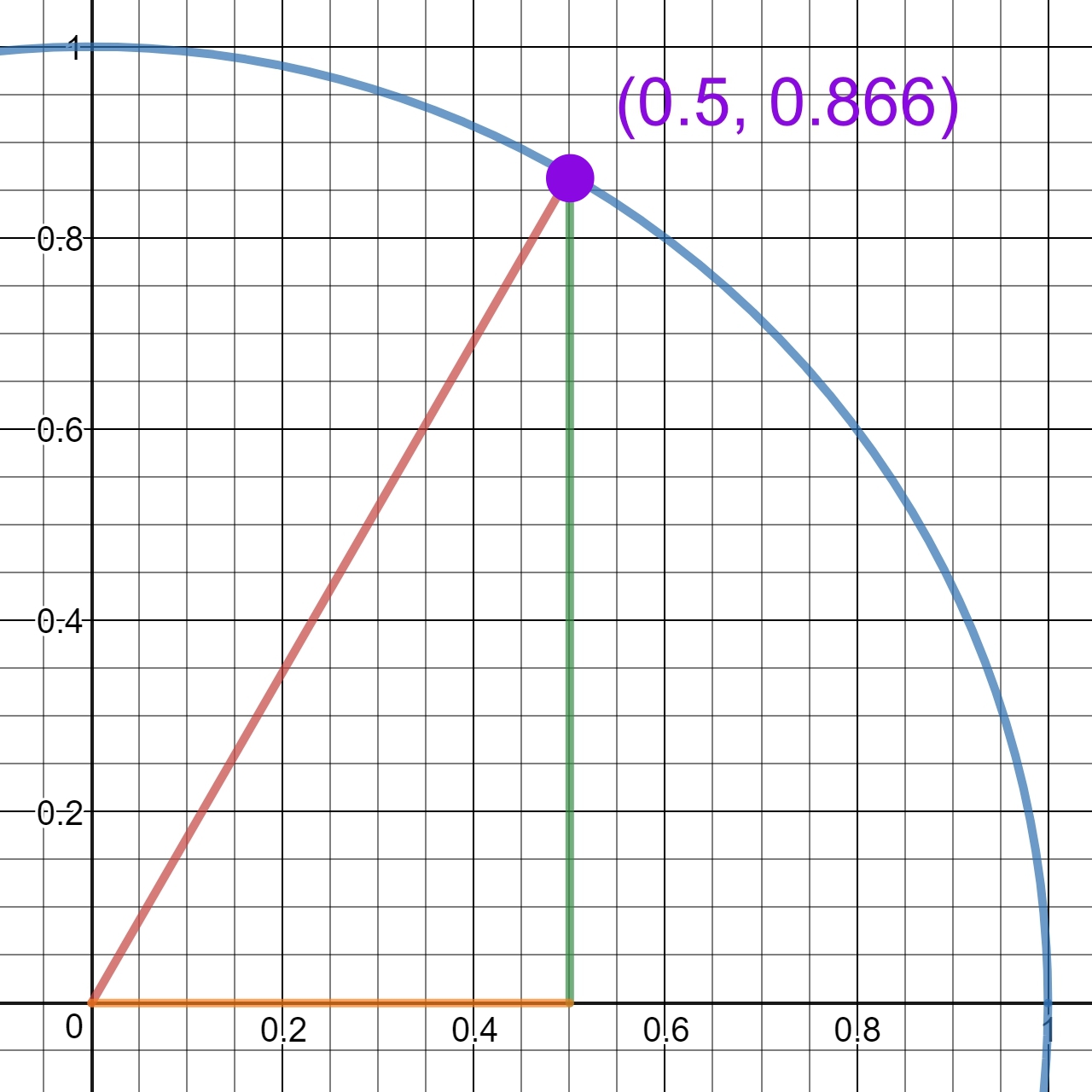
Autre exemple d'un point du cercle (image ci-dessous) qui a pour valeur x = 0,7071 et y = 0,7071.
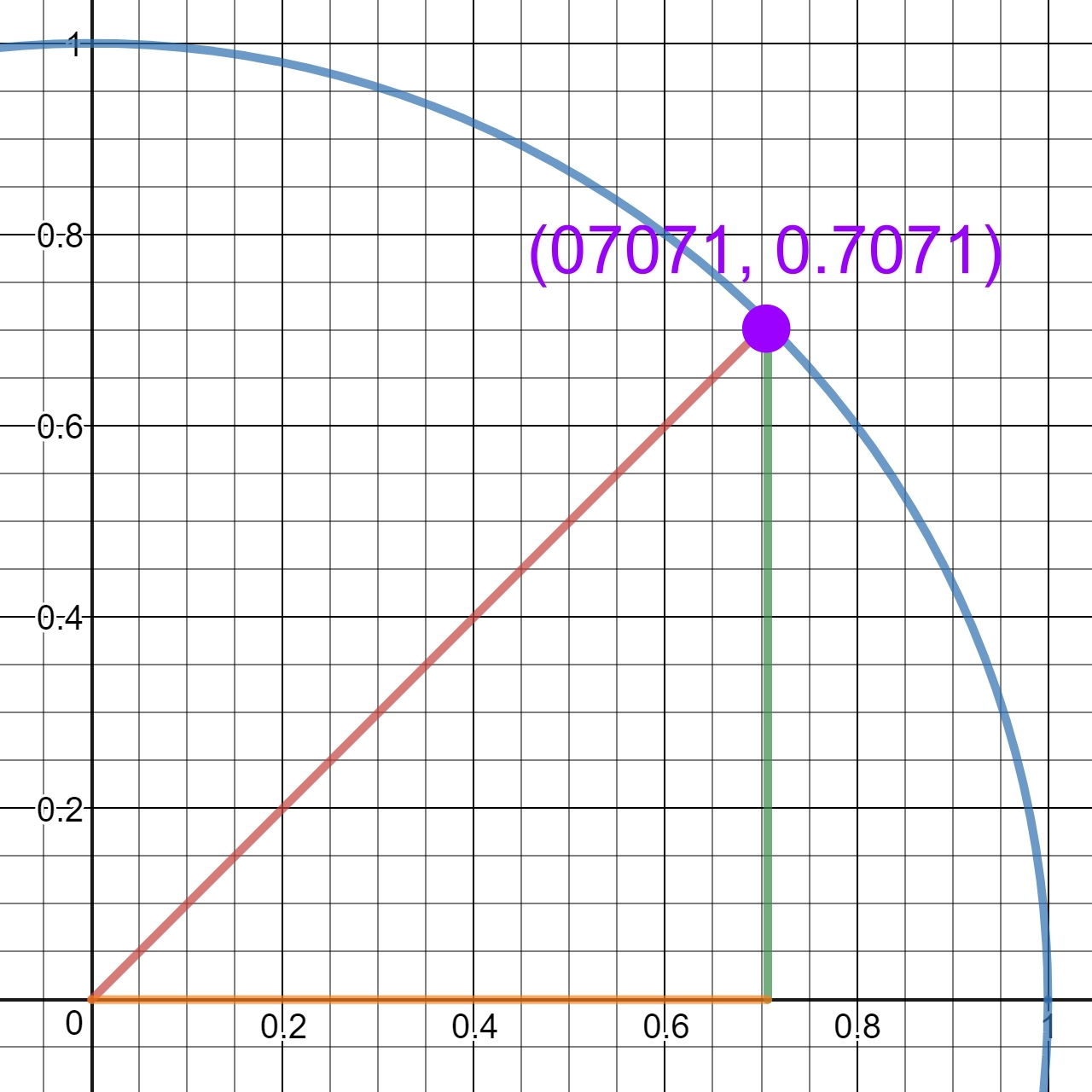
Le segment orange (valeur de x), le segment vert (valeur de y) et le segment rouge (rayon du cercle) font ensemble un triangle rectangle.
Le rayon est l'hypoténuse de ce triangle rectangle.
Le segment orange et le segment vert représentent respectivement les valeurs x et y de chaque point.
Rappel du théorème de Pythagore: le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Application du théorème:
a) pour le premier point:
0,5² + 0,866² = 1²
0,25 + 0,7499 = 1
b) pour le deuxième point:
0,7071² + 0,7071² = 1²
0,49999 + 0,49999 = 1
Nous pouvons donc écrire pour un cercle au centre du repère orthonormé et ayant "r" comme rayon:
est l'équation du cercle
(dans un repère orthonormé)
Ci-dessous, un exemple de génération d'un cercle (de rayon = 2) dans un repère orthonormé avec la calculatrice graphique DESMOS (outil libre disponible sur Internet) à partir de l'équation du cercle.
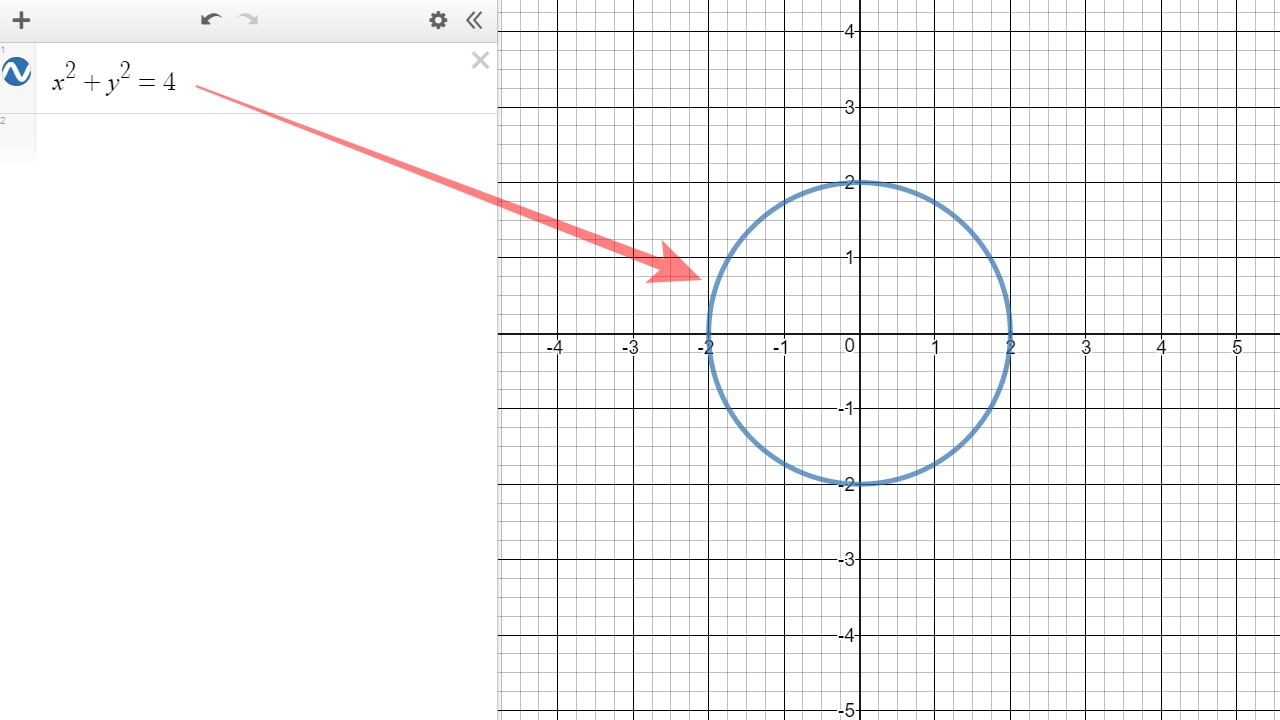
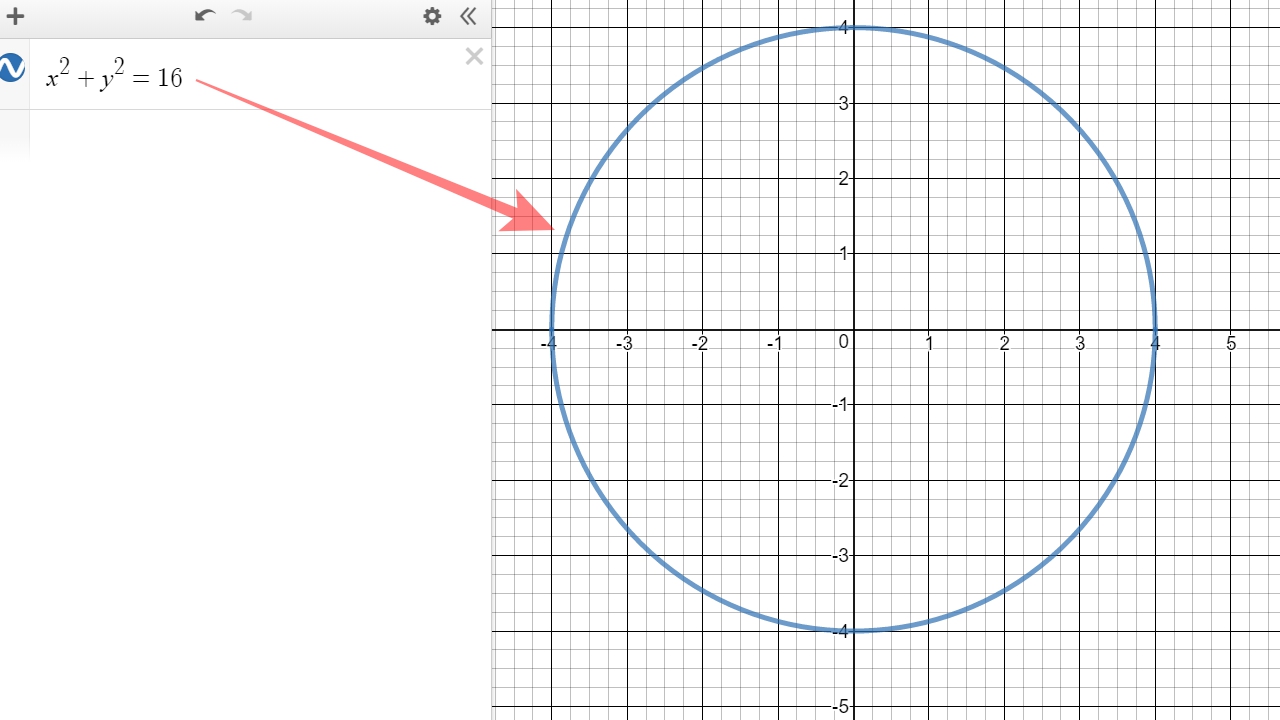
Ci-dessous, un exemple de génération d'un cercle (de rayon = 4).
• • •
• •
•
• •
•
