
fonction
dérivée
d'une
fonction
dérivée
d'une
fonction

Plan de la page (avec un accès direct en utilisant les flèches oranges):
• Définition ............ -->
• Comprendre ............ -->
• Autres exemples ....... -->
•••
D É F I N I T I O N
La fonction dérivée est une fonction mathématique qui associe à chaque réel x d'une fonction f le coefficient directeur de la tangente en un point de la courbe représentative de f.
La définition (ci-dessus) est la meilleure explication pour définir ce qu'est une fonction dérivée. Et pourtant elle peut paraître une peu absconse.
Aussi, l'exemple qui suit devrait apporter toute la lumière sur cette excellente définition (car elle colle parfaitement au rôle de la fonction dérivée).
•••
C O M P R E N D R E
P A R L ' E X E M P L E
Première étape: qu'est-ce qu'une tangente?
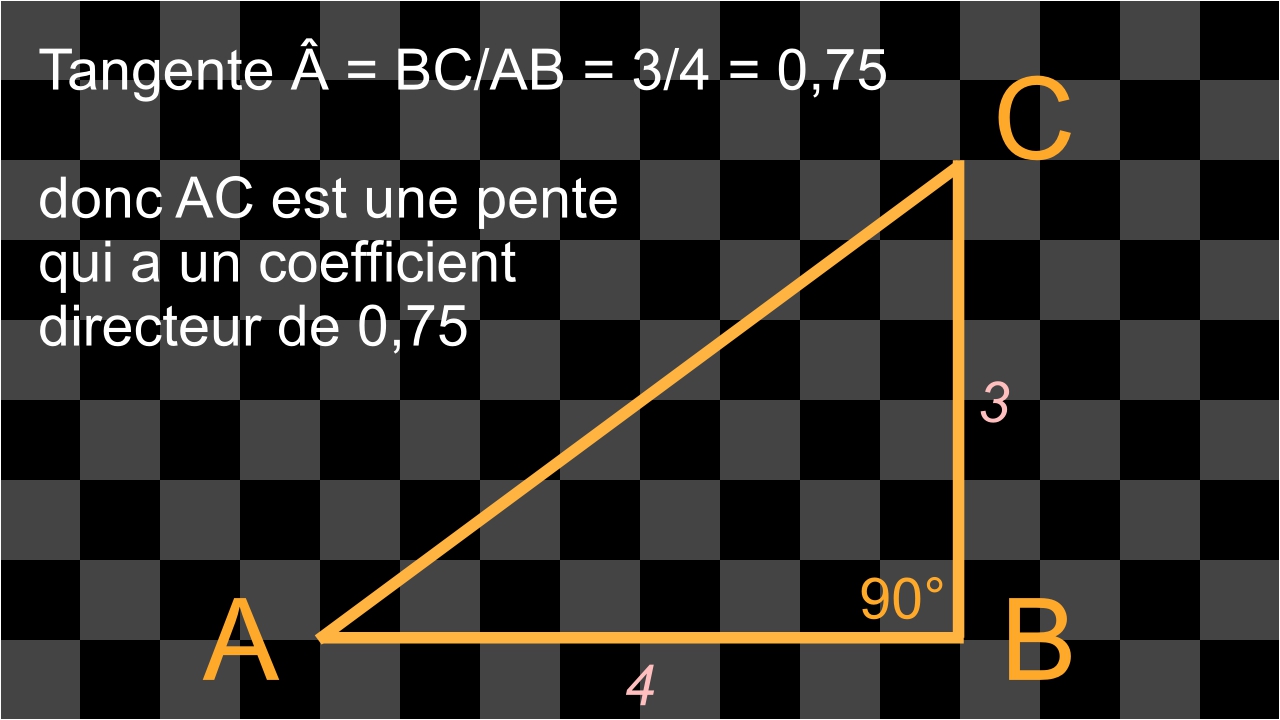
Soit un triangle rectangle ABC (voir ci-dessous). L'angle B fait 90° donc AC est l'hypoténuse. En considérant l'angle A, le côté BC est son côté opposé et le côté AB est son côté adjacent.
La tangente d'un angle (non droit) est le rapport entre le côté opposé et le côté adjacent à cet angle.
Donc la tangente de l'angle A est BC/AB, ce qui donne dans notre exemple 3/4 (ou 0,75).
La valeur 0,75 (BC/AB) n'a pas d'unités car c'est un rapport (rappel: 10 mètres divisés par 5 mètres donnent 2 et non pas 2 mètres).
Ce rapport est la tangente de l'angle A et la valeur 0,75 représente le COEFFICIENT DIRECTEUR de la pente AC (AB étant la référence).
Deuxième étape: qu'est-ce qu'une tangente à une courbe?
La tangente à une courbe en un de ses points est une droite qui "touche" la courbe au plus près au voisinage de ce point. La courbe et sa tangente forment alors un angle nul en ce point (source de cette définition: Wikipedia).
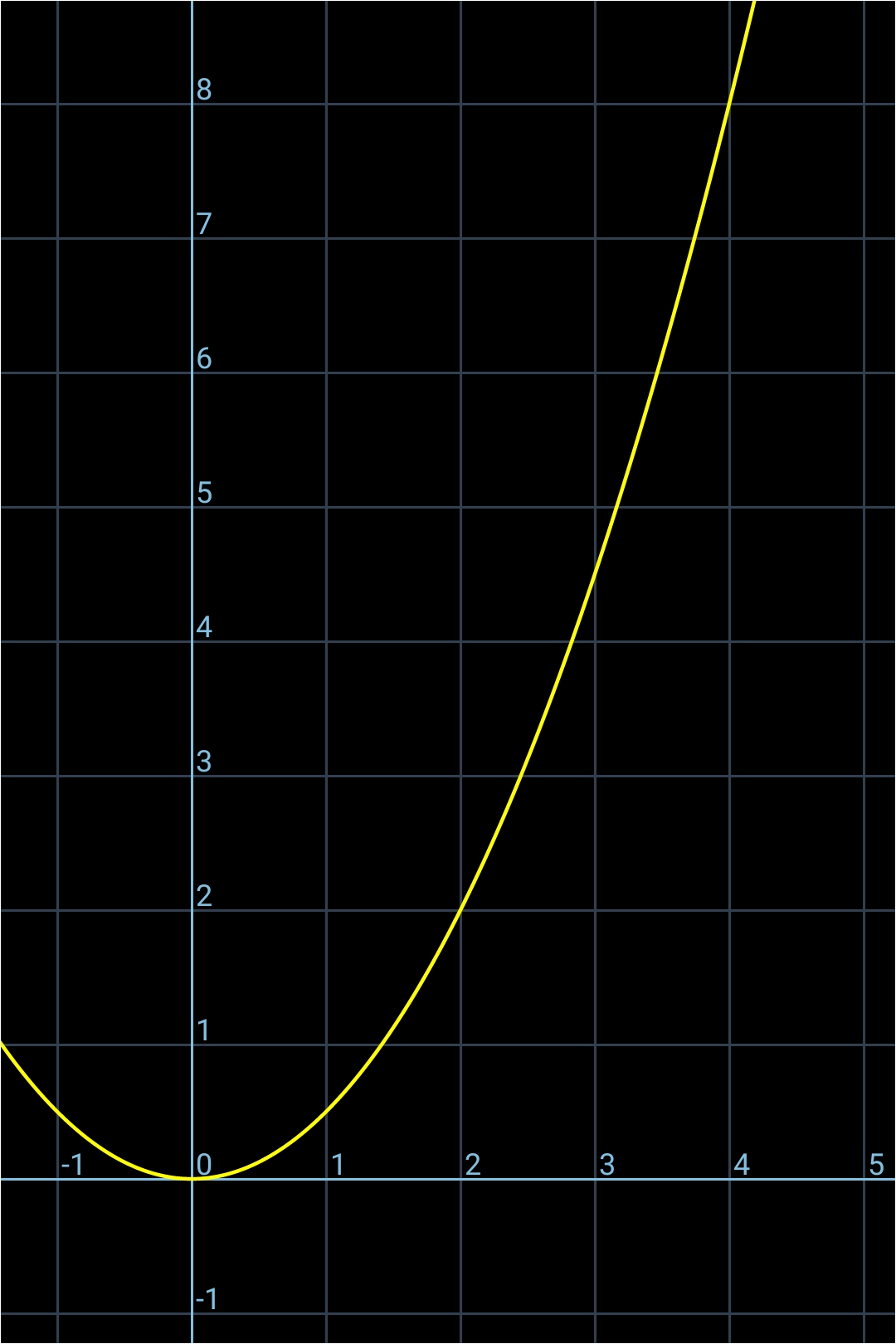
Soit la fonction y = (1/2)x² qui génère la courbe ci-dessous:
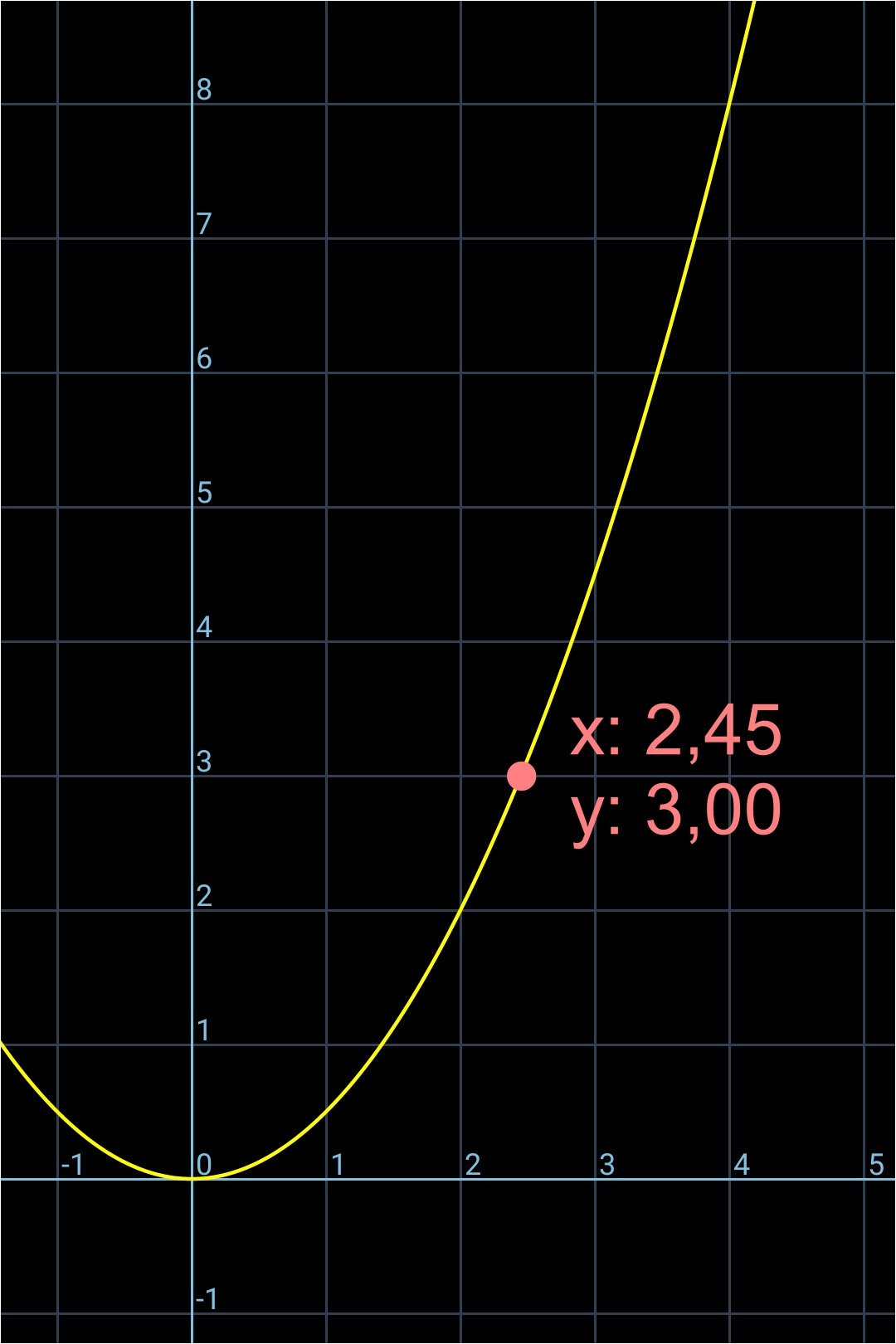
Soit un point sur la courbe aux coordonnées x = 2,45 et y = 3,00 ci-dessous:
On trace la tangente de ce point (en vert et en pointillé sur l'image ci-dessous):
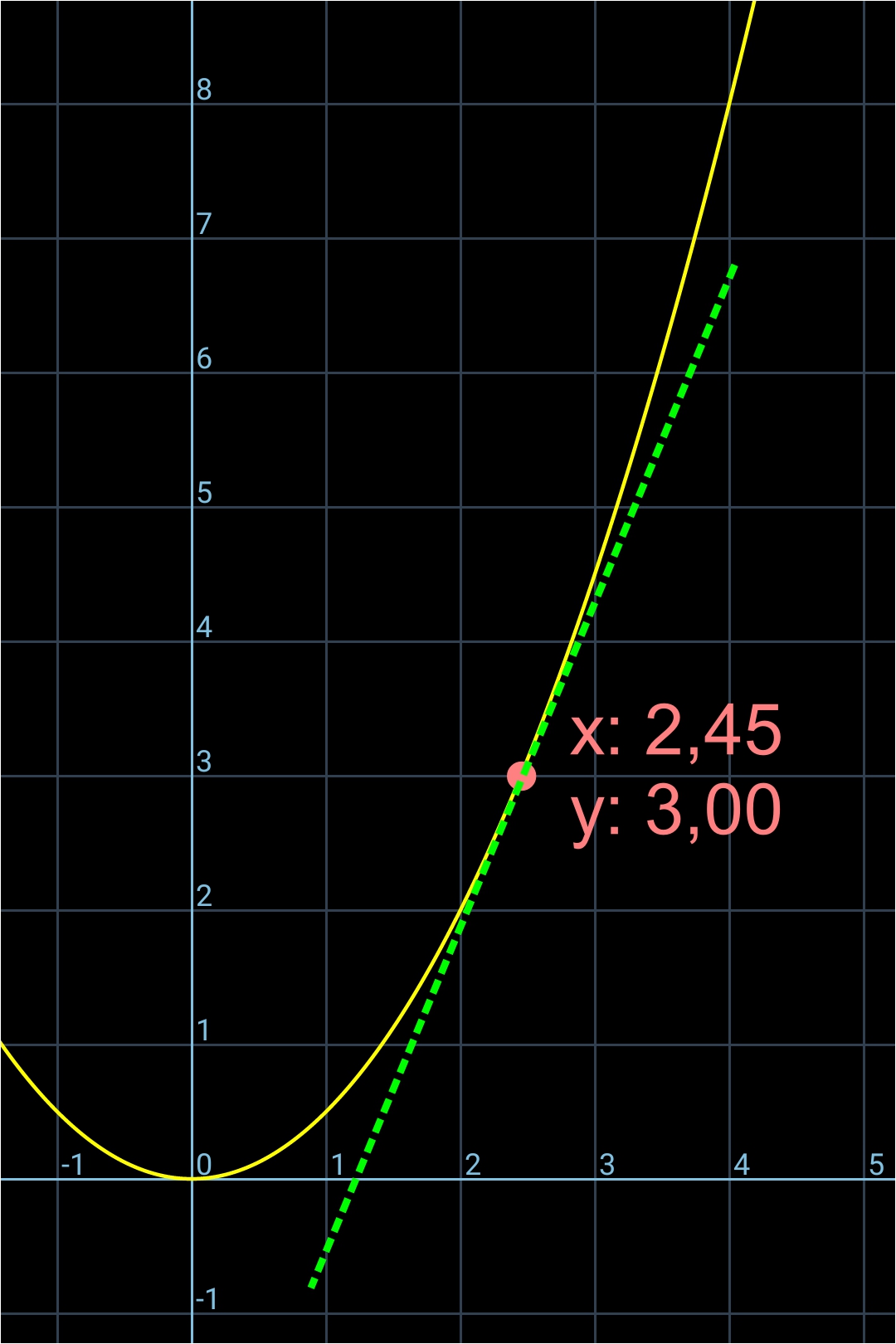
Sur l'image qui suit, on va calculer le coefficient directeur de la pente de cette tangente en faisant le rapport de BC/AB:
• AB = 2,75
• BC = 6,75
• BC/AB = 6,75/2,75 = 2,45
• coefficient directeur = 2,45
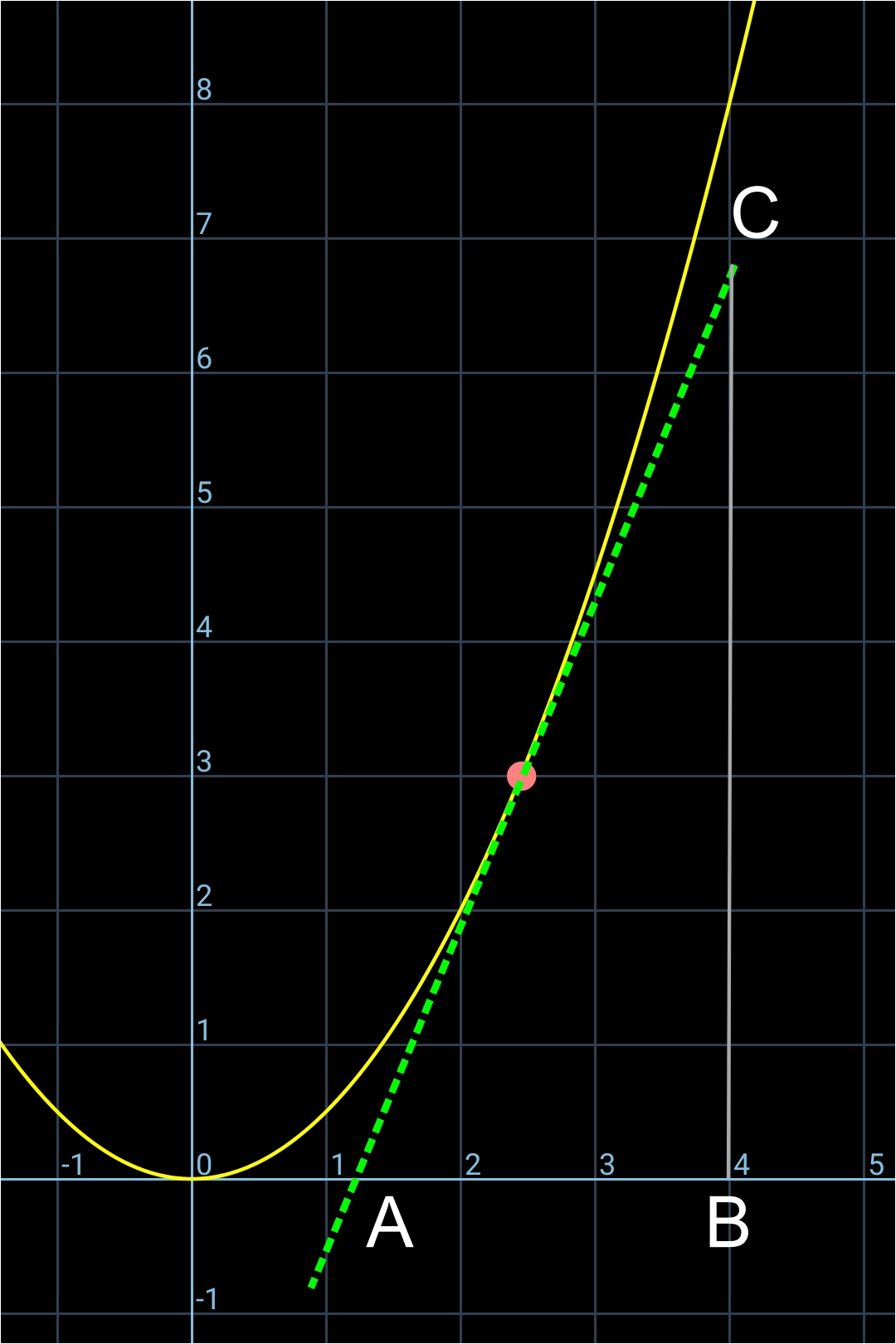
Soit un autre point sur la courbe aux coordonnées x = 4,00 et y = 8,00 ci-dessous:
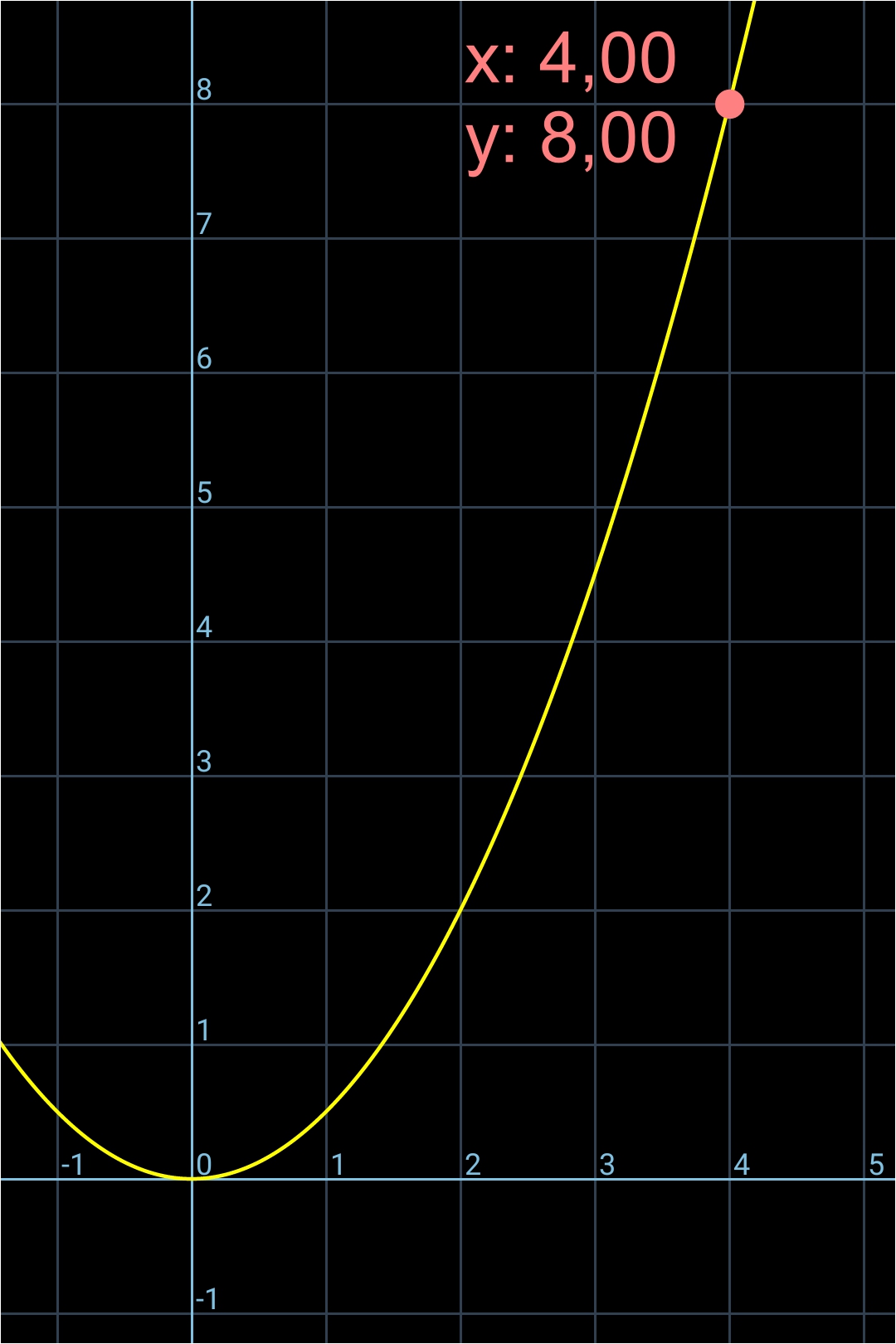
On trace la tangente de ce point (en vert et en pointillé sur l'image ci-dessous):
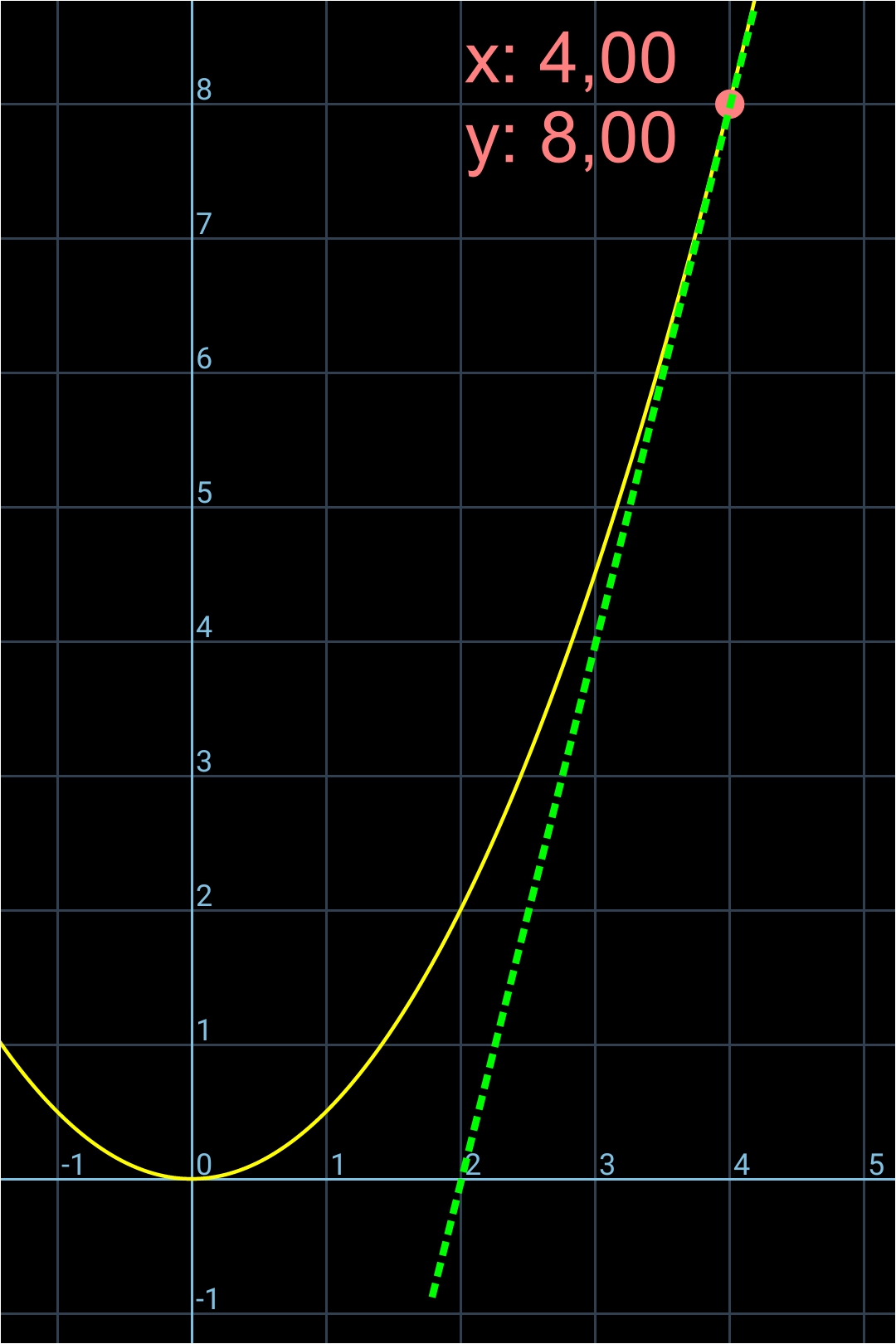
Sur l'image qui suit, on va calculer le coefficient directeur de la pente de cette tangente en faisant le rapport de BC/AB:
• AB = 2,00
• BC = 8,00
• BC/AB = 8,00/2,00 = 4
• coefficient directeur = 4
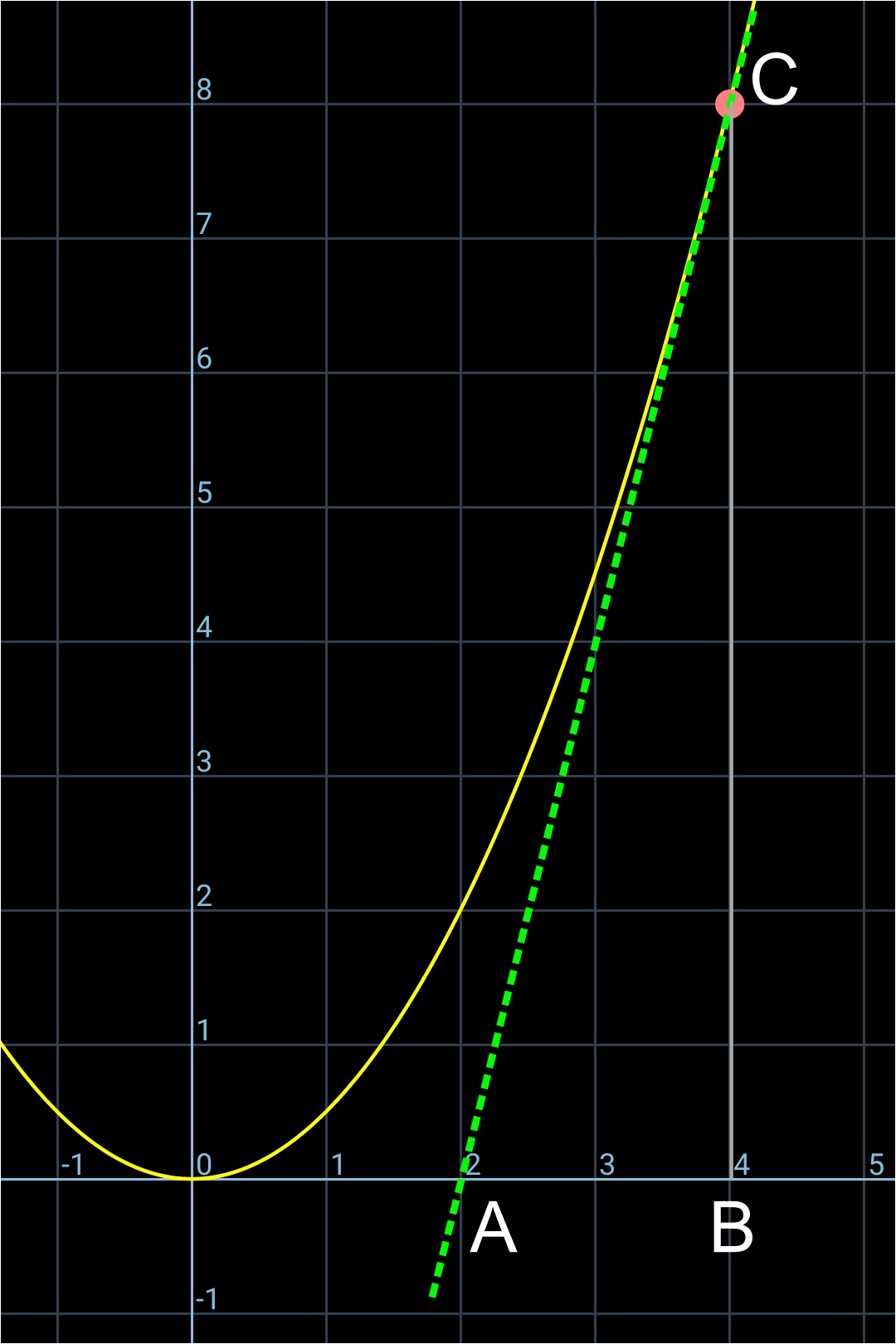
Troisième étape: on abandonne la tangente (pour un petit moment) et on va calculer la fonction dérivée de la fonction y = (1/2)x².
Pour calculer la fonction dérivée (appelée y') d'une fonction (appelée y), on va procéder en quatre actions:
Les quatre actions décrites ci-dessous sont très importantes et fondamentales car elles consistent à ajouter un accroissement à x et à observer son impact (sa "dérive"!) sur y.
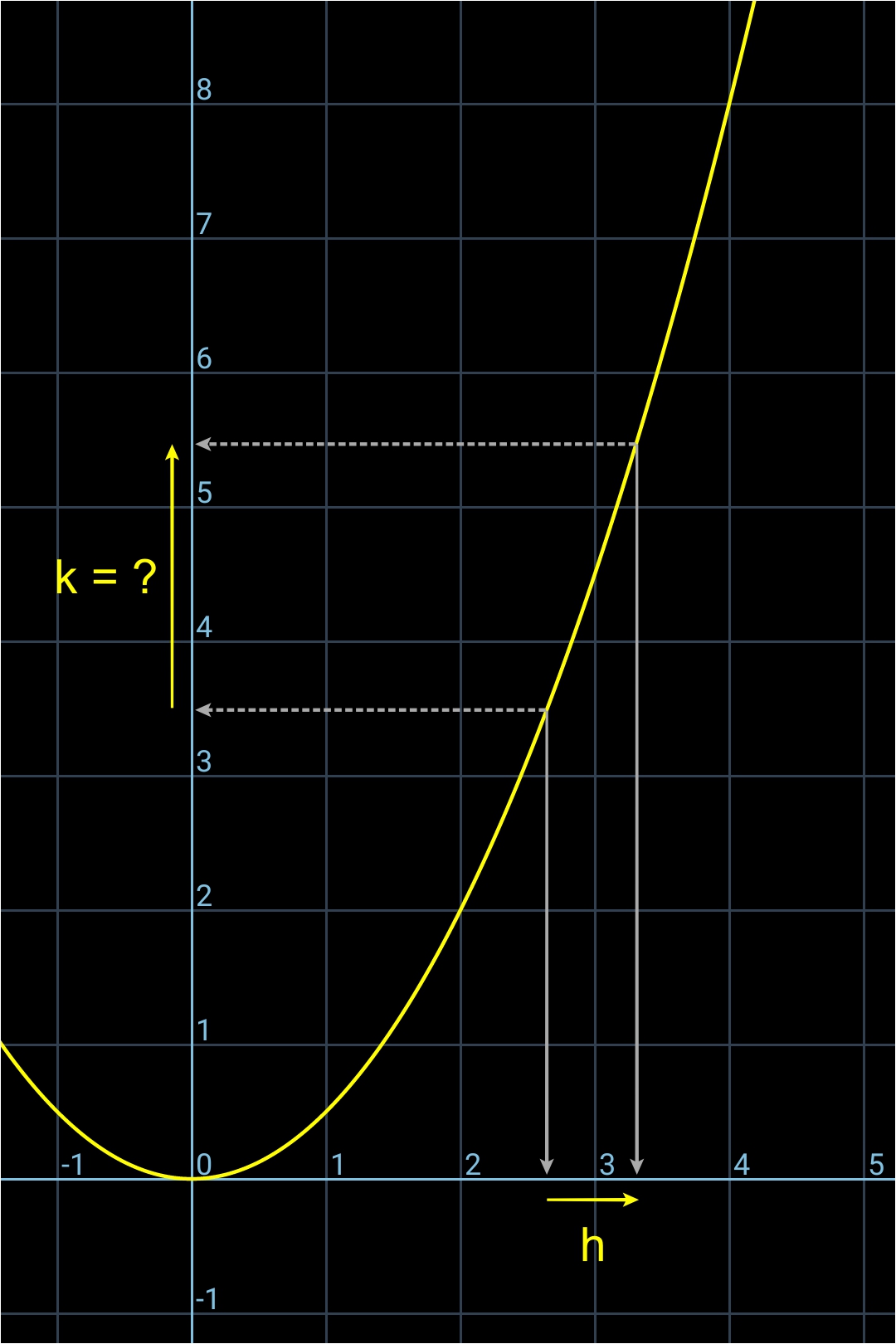
1) donner à x un accroissement h
2) calculer l'accroissement k
sur y (conséquence de h)
3) faire le rapport k/h et le
simplifier
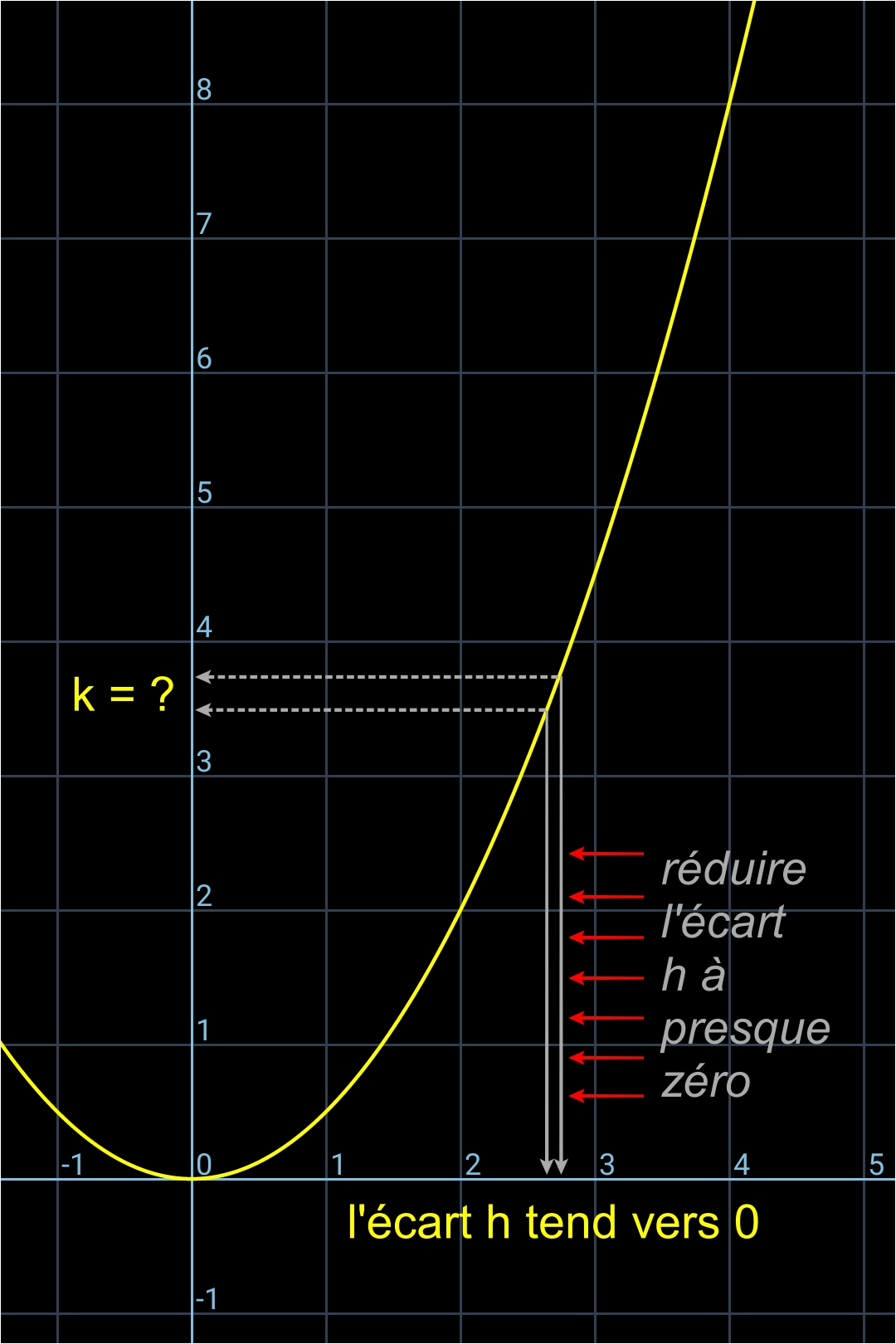
4) (re)calculer ce rapport quand
h tend vers 0
Avant de mettre en application ces quatre actions, les deux images ci-dessous montrent:2) calculer l'accroissement k
sur y (conséquence de h)
3) faire le rapport k/h et le
simplifier
4) (re)calculer ce rapport quand
h tend vers 0
a) l'action de donner à x un accroissement h et de calculer k qui est l'incidence sur y de cet accroissement (voir la première image, ci-dessous),
b) l'action de tendre h vers zéro (voir la deuxième image, ci-dessous).
IL FAUT BIEN NOTER QUE LE RAPPORT K/H N'EST RIEN D'AUTRE QUE LE COEFFICIENT DIRECTEUR DE LA PENTE ASSOCIÉE À LA TANGENTE DE LA COURBE EN UN POINT.
Calcul (en appliquant les quatre actions) de la fonction dérivée de la fonction
• y = (1/2)x² = 0,5x²
• y + k = 0,5(x + h)²
• y + k = 0,5(x² + 2xh + h²)
• y + k = 0,5x² + 0,5*2xh + 0,5h²
• y + k = 0,5x² + xh + 0,5h²
comme y = 0,5x² ==>
• 0,5x² + k = 0,5x² + xh + 0,5h²
• k = 0,5x² - 0,5x² + xh + 0,5h²
• k = xh + 0,5h²
• k = h(x + 0,5h)
• k/h = x + 0,5h
• k/h = x + 0 (*)
• k/h = y' = x
(*) Note: 0,5h devient 0 car h tend vers 0 et par conséquence 0,5h tend également vers 0.
On obtient alors:
y' = x
qui est la fonction dérivée de la fonction y = (1/2)x².
On reporte sur le graphe la fonction dérivée (en rouge, ci-dessous):
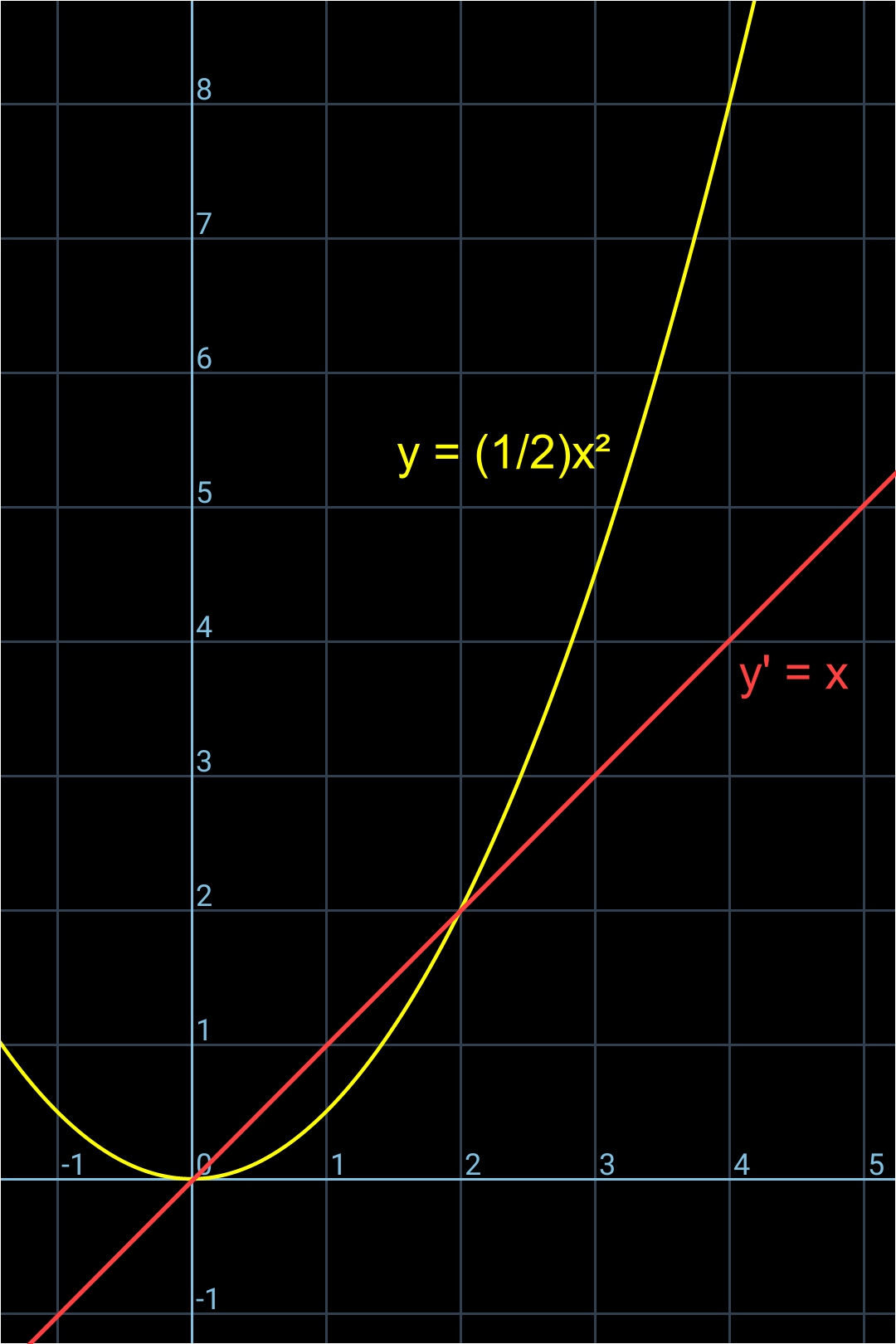
Quatrième étape: l'image ci-dessous montre le lien entre la fonction dérivée y' et le coefficient directeur des tangentes de chaque point de la courbe de la fonction y:
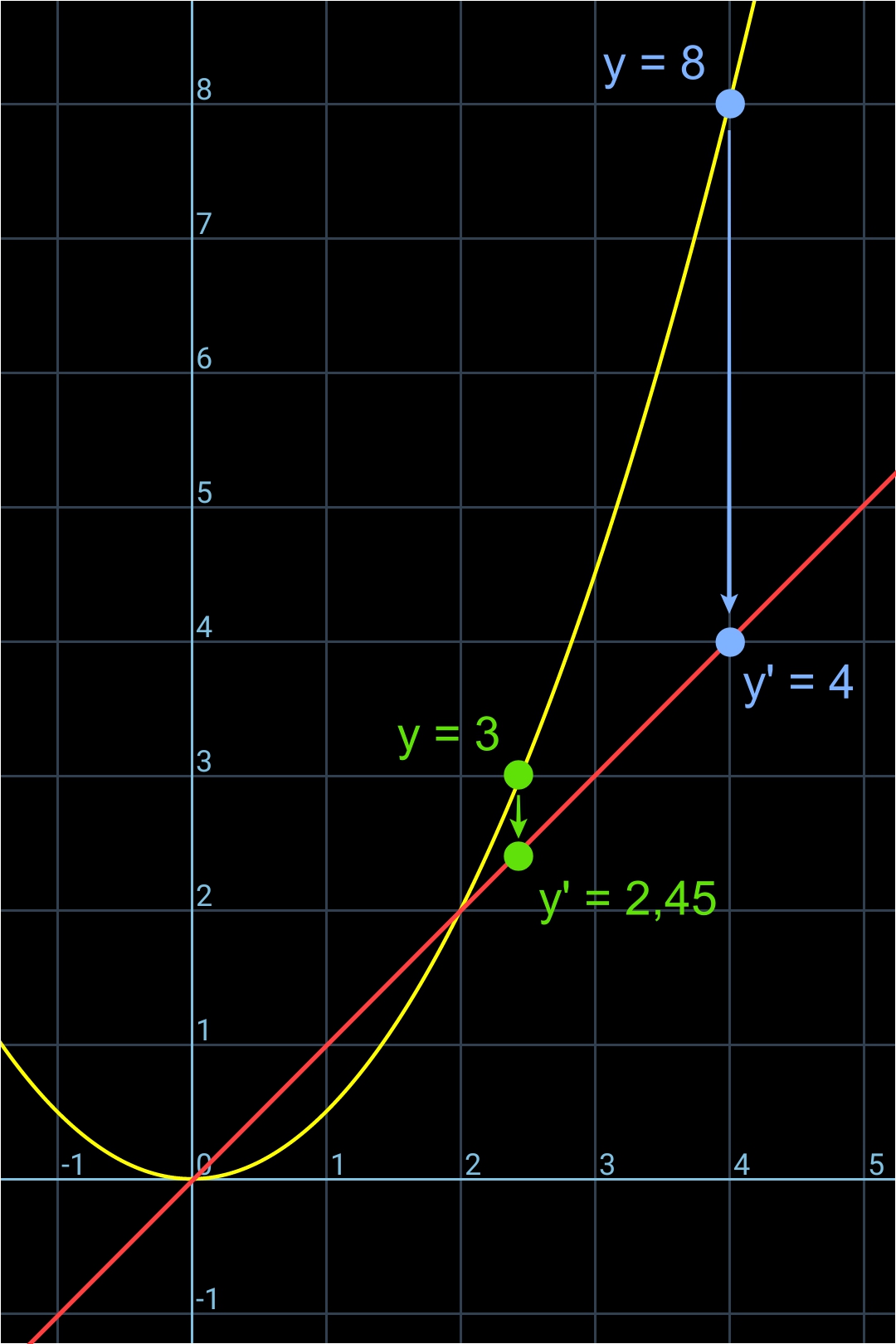
•••
A U T R E S
E X E M P L E S
Liste des exemples (avec un accès direct en utilisant les flèches oranges):
• y = ax + b ........... -->
• y = x² ............... -->
• y = x³ ............... -->
• y = 1/x .............. -->
Exemple #1 du calcul de la fonction dérivée de la fonction
• y = ax + b
• y + k = a(x + h) + b
• y + k = ax + ah + b
comme y = ax + b ==>
• ax + b + k = ax + ah + b
• k = ax - ax + ah + b - b
• k = ah
• k/h = a
la fonction y = ax + b a pour fonction dérivée:
y' = a
Exemple #2 du calcul de la fonction dérivée de la fonction
• y = x²
• y + k = (x + h)²
• y + k = x² + 2xh + h²
comme y = x² ==>
• x² + k = x² + 2xh + h²
• k = x² - x² + 2xh + h²
• k = 2xh + h²
• k = h(2x + h)
• k/h = 2x + h
sachant que h tend vers 0, la fonction y = x² a pour fonction dérivée:
y' = 2x
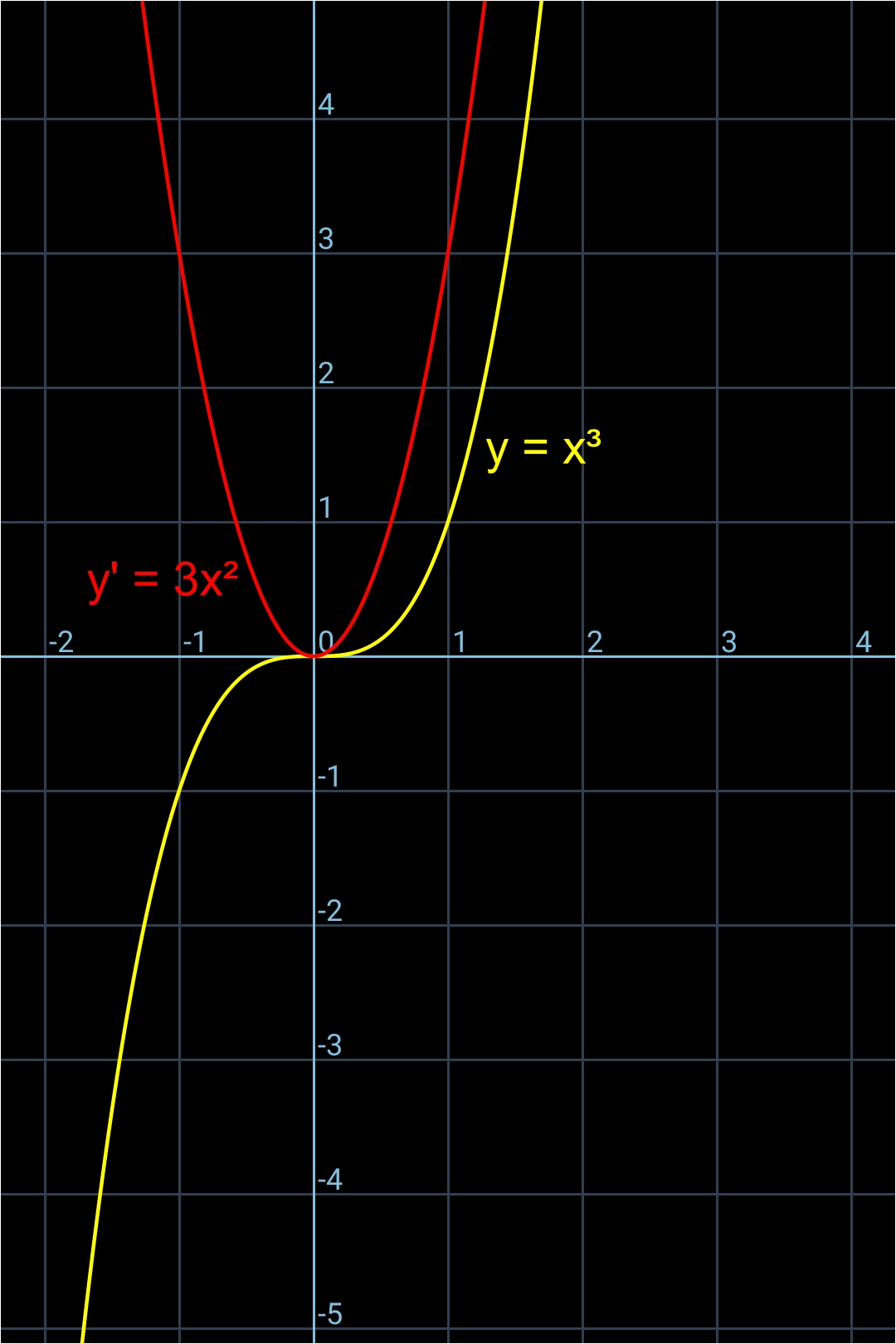
Exemple #3 (avec le graphe correspondant) du calcul de la fonction dérivée de la fonction
• y = x³
• y + k = (x + h)³
• y + k = x³ + 3x²h + 3xh² + h³
comme y = x³ ==>
• x³ + k = x³ + 3x²h + 3xh² + h³
• k = x³ - x³ + 3x²h + 3xh² + h³
• k = 3x²h + 3xh² + h³
• k = h(3x² + 3xh + h²)
• k/h = 3x² + 3xh + h²
• k/h = 3x²
sachant que h tend vers 0, alors 3xh et h² tendent vers 0 et donc la fonction y = x³ a pour fonction dérivée:
y' = 3x²
Ci-dessous la représentation graphique de la fonction (y = x³) et sa fonction dérivée (y' = 3x²):
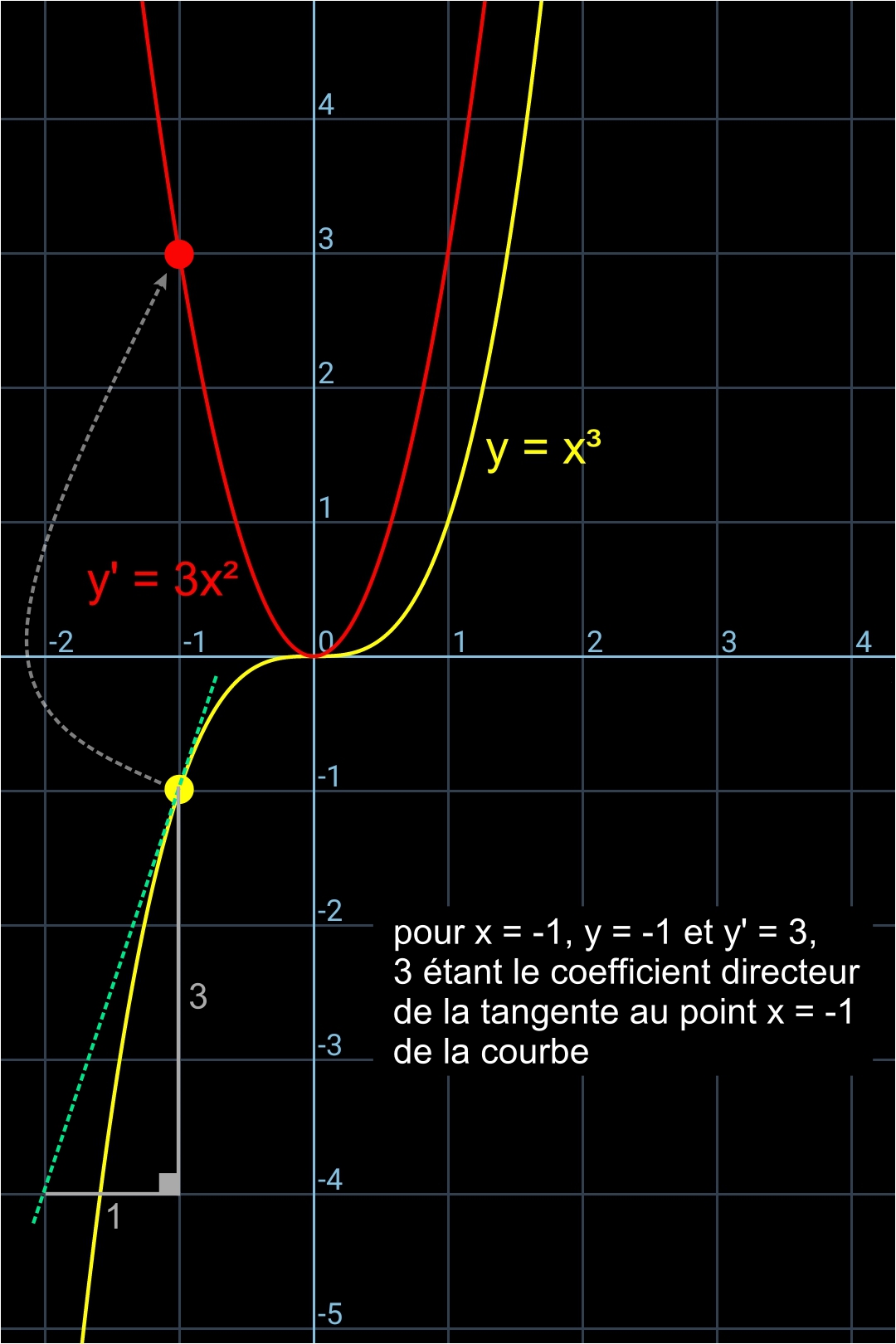
Et ci-dessous l'illustration de la dérivée d'un point de la courbe y = x³:
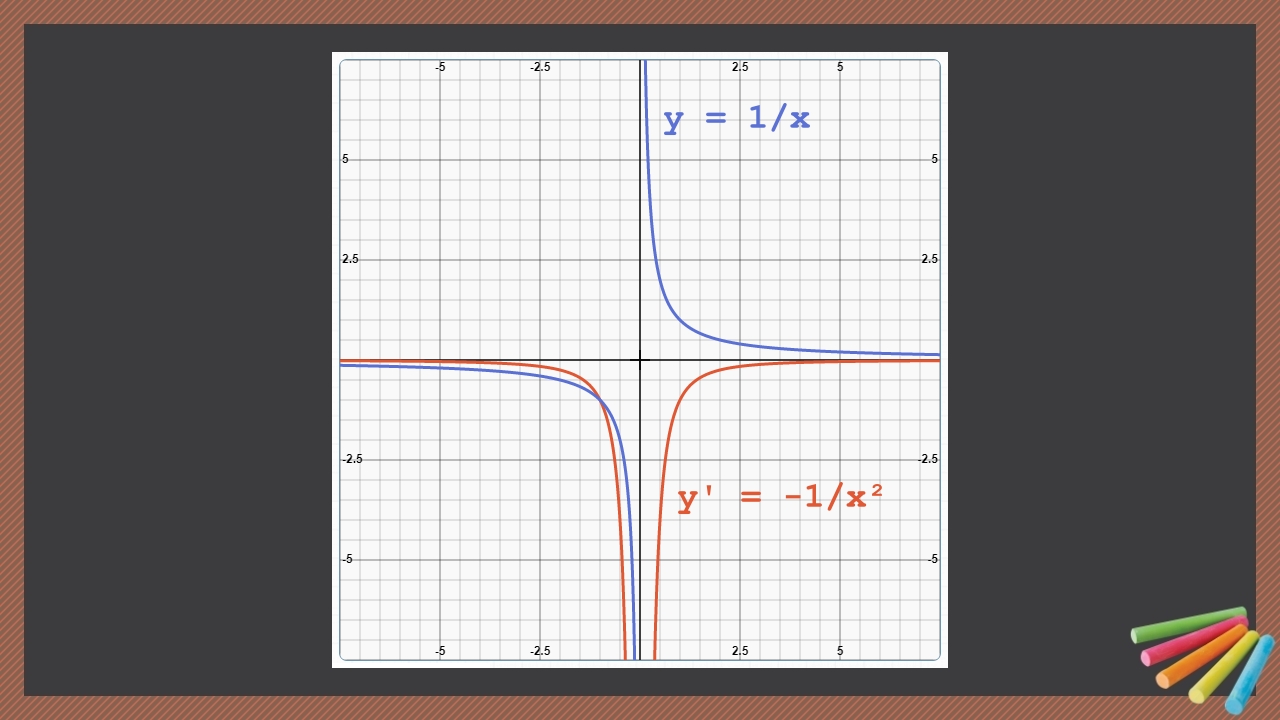
Exemple #4 (ajouté le 23-10-2019) du calcul de la fonction dérivée de la fonction

• • •
• •
•
• •
•
