
résolution par
la géométrie
des équations
du second degré
(si a=1 et c<0)
la géométrie
des équations
du second degré
(si a=1 et c<0)


modèle de base: ax² + bx + c = 0
• si a=1, on obtient x² + bx + c = 0
• si c<0, on obtient x² + bx - c = 0
• qui peut s'écrire x² + bx = c
• qui peut se matérialiser ainsi:
- x² = une surface (aire1)
- bx = une surface (aire2)
- c = aire1 + aire2
- voir ci-dessous (5 planches)
planche 1
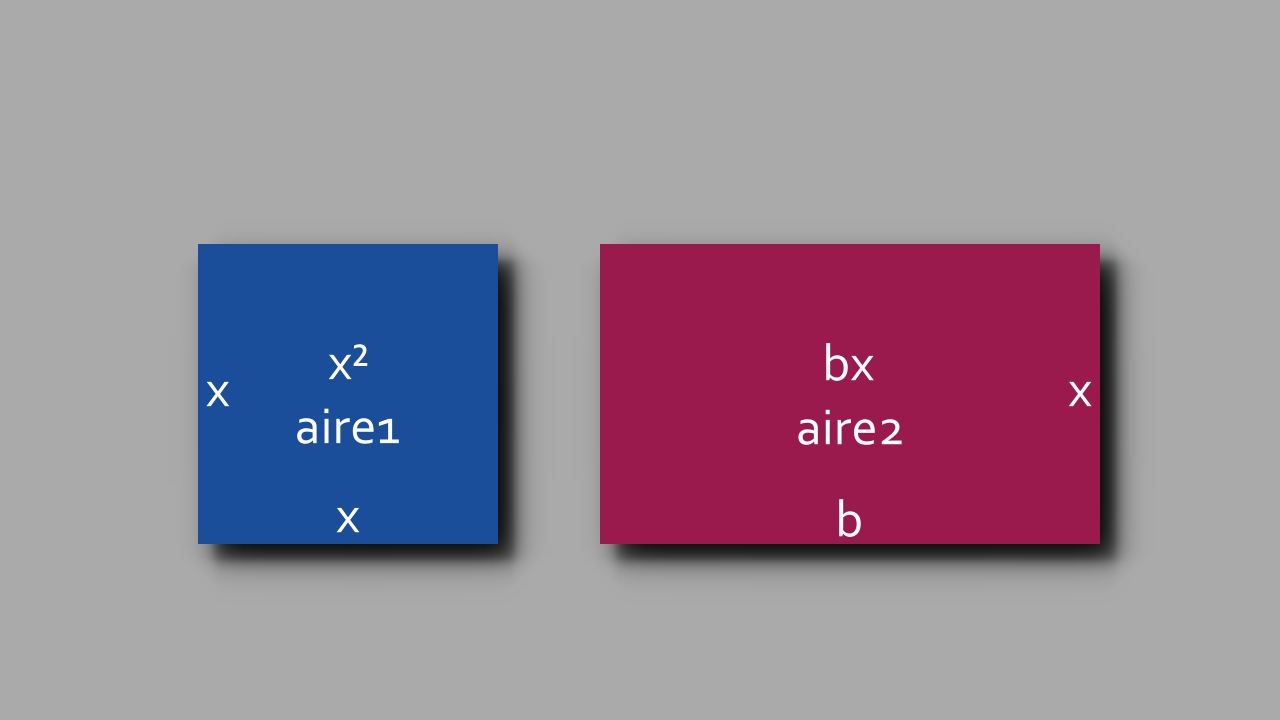
planche 2

planche 3
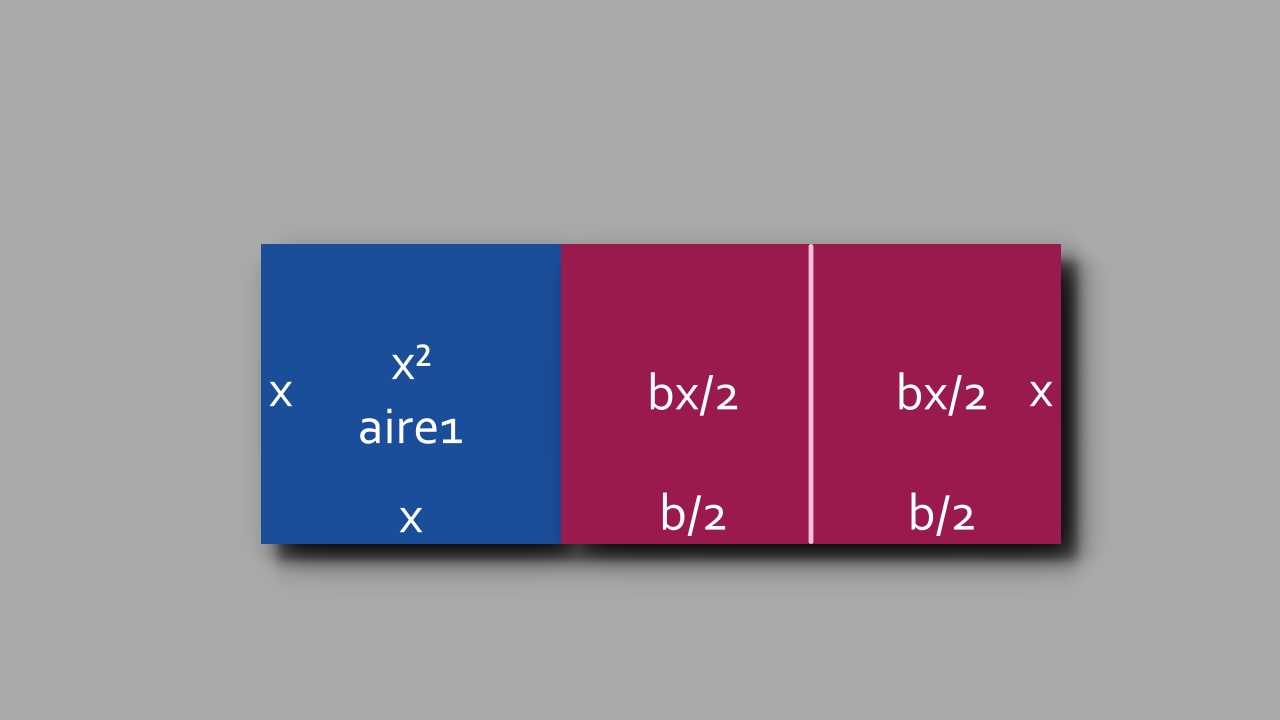
planche 4
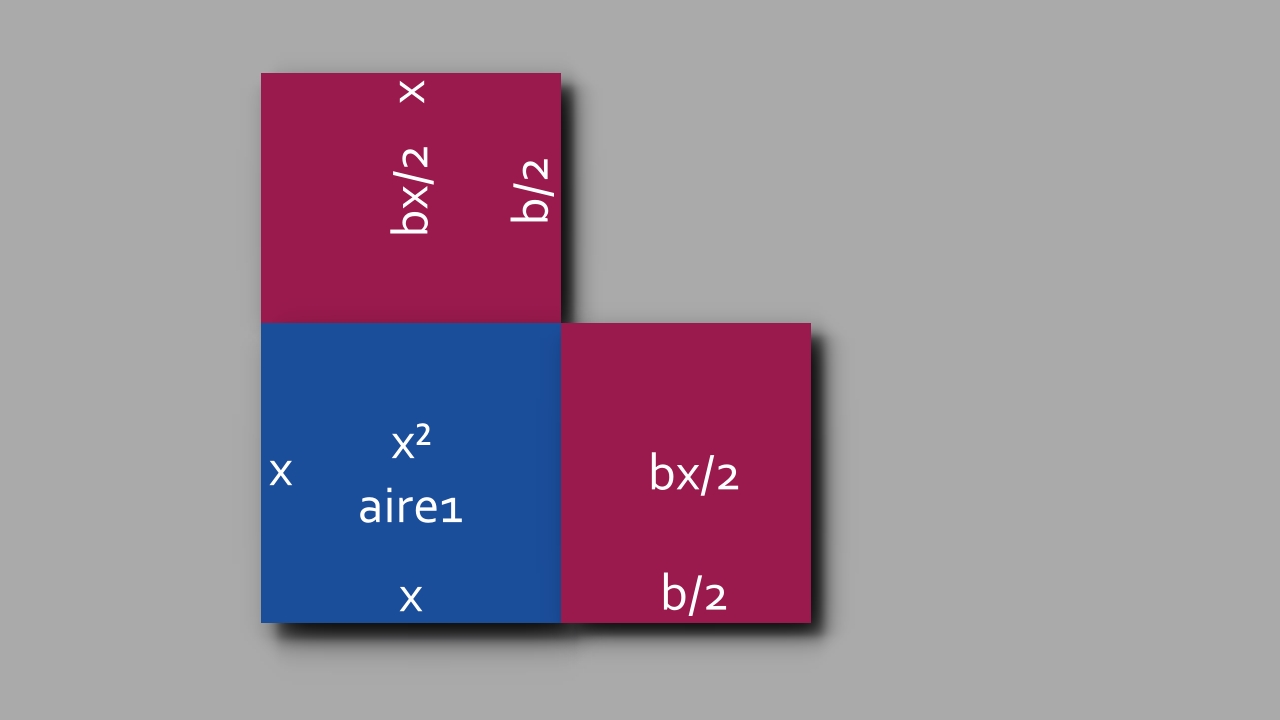
planche 5
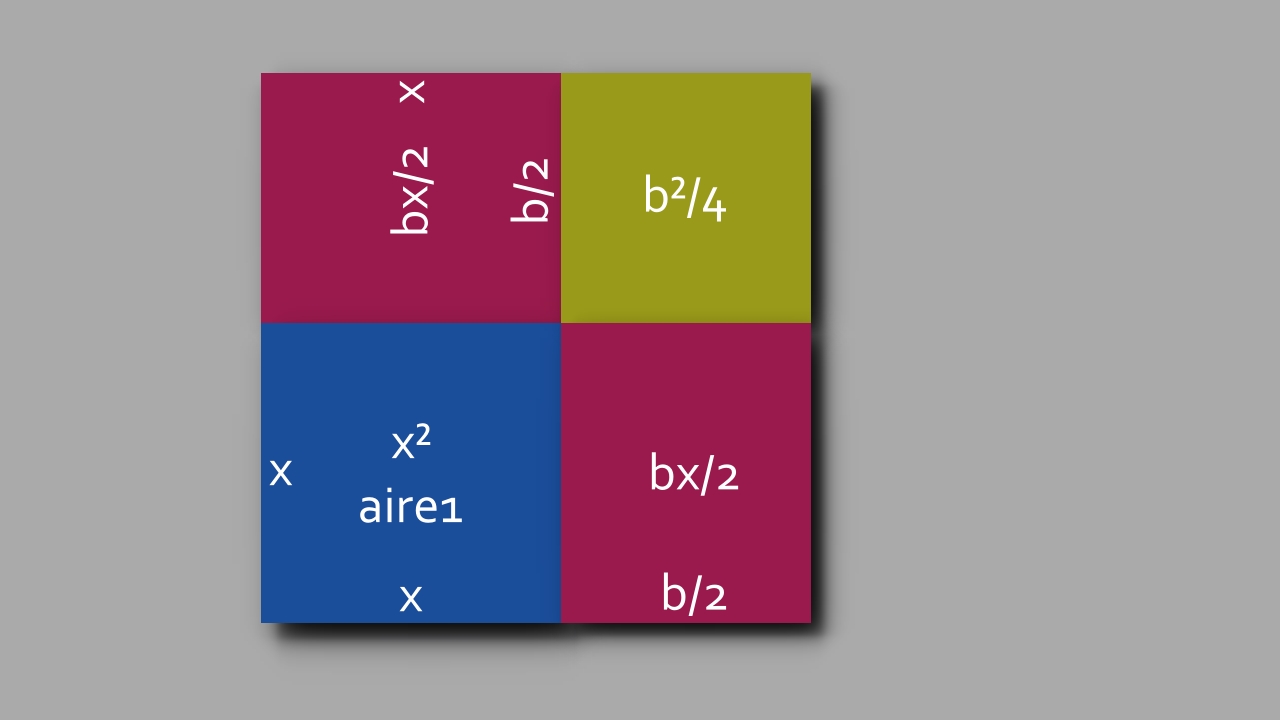
sur la planche 5 (ci-dessus), l'aire de c est égale à:
• c = (x + b/2)² - b²/4
• c = (x + b/2)² - (b/2)²
• c + (b/2)² = (x + b/2)²
ou encore (permutation):
• (x + b/2)² = c + (b/2)²
et ainsi on obtient:
• un carré: (x + b/2)²
• une constante: c + (b/2)²
note: b et c étant des paramètres (valeurs connues), c+(b/2)² peut donc être évalué (constante)
-----------------------------
--- application (exemple) ---
-----------------------------
sur le modèle: x² + bx = c
soit à résoudre: x² + 3x = 28
en appliquant:
• (x + 3/2)² = 28 + (3/2)²
• (x + 3/2)² = 28 + 2,25
• (x + 3/2)² = 30,25
• (x + 3/2) = 5,5
• (x + 1,5) = 5,5
• x = 5,5 - 1,5
• x = 4

(page en construction)
(page en construction)
(page en construction)
• • •
• •
•
• •
•
