
calculer
l'aire d'un
polygone régulier
à partir de son
périmètre
l'aire d'un
polygone régulier
à partir de son
périmètre

planche 1

planche 2
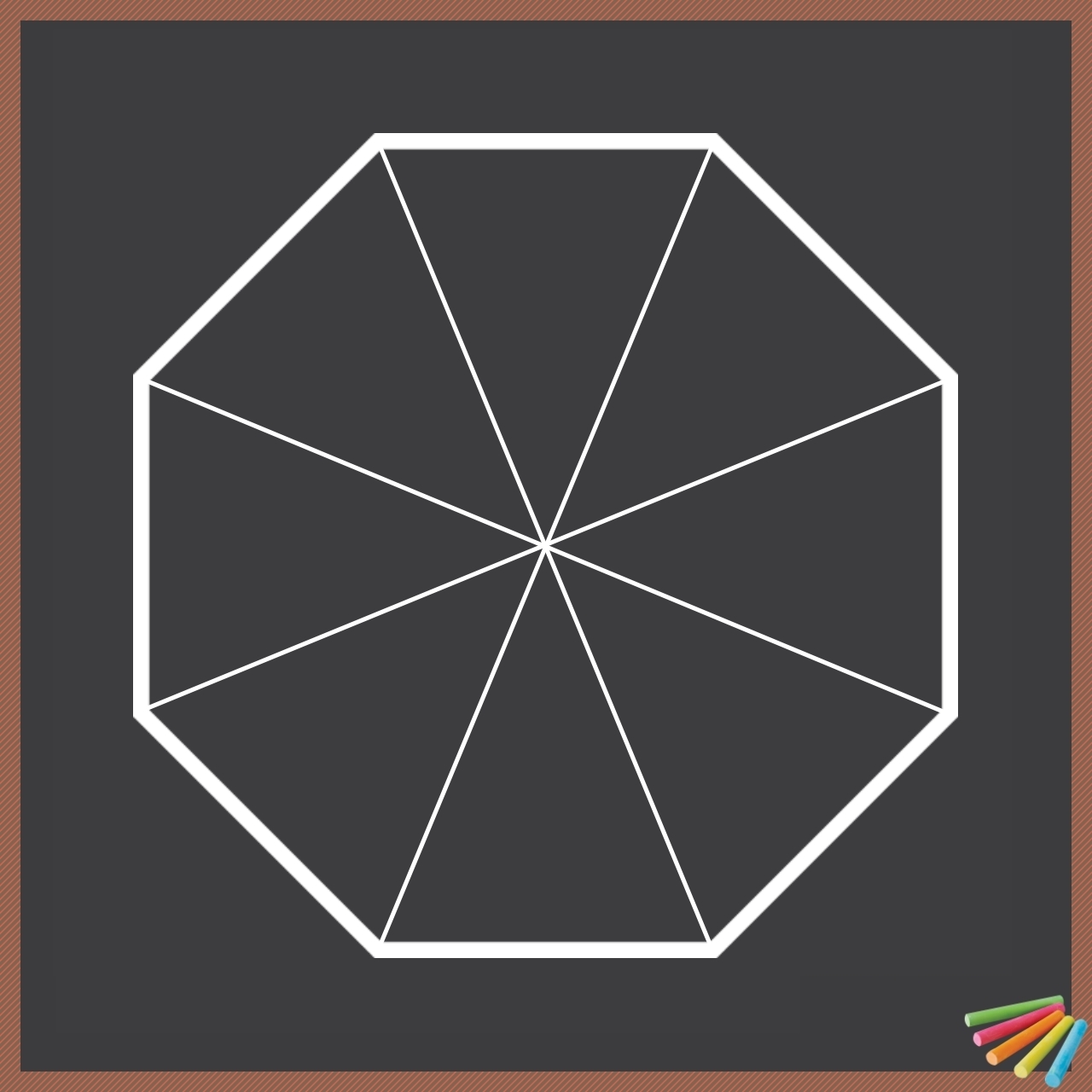
planche 3
Le but de cette page est le calcul de l'aire d'un polygone régulier et convexe (voir planche 1) à partir de deux données:
• le périmètre
• le nombre de côtés (>4)

Un polygone régulier et convexe est une somme de triangles isocèles et identiques.
Par exemple, un octogone régulier et convexe comprend 8 triangles isocèles et identiques (voir planche 2).
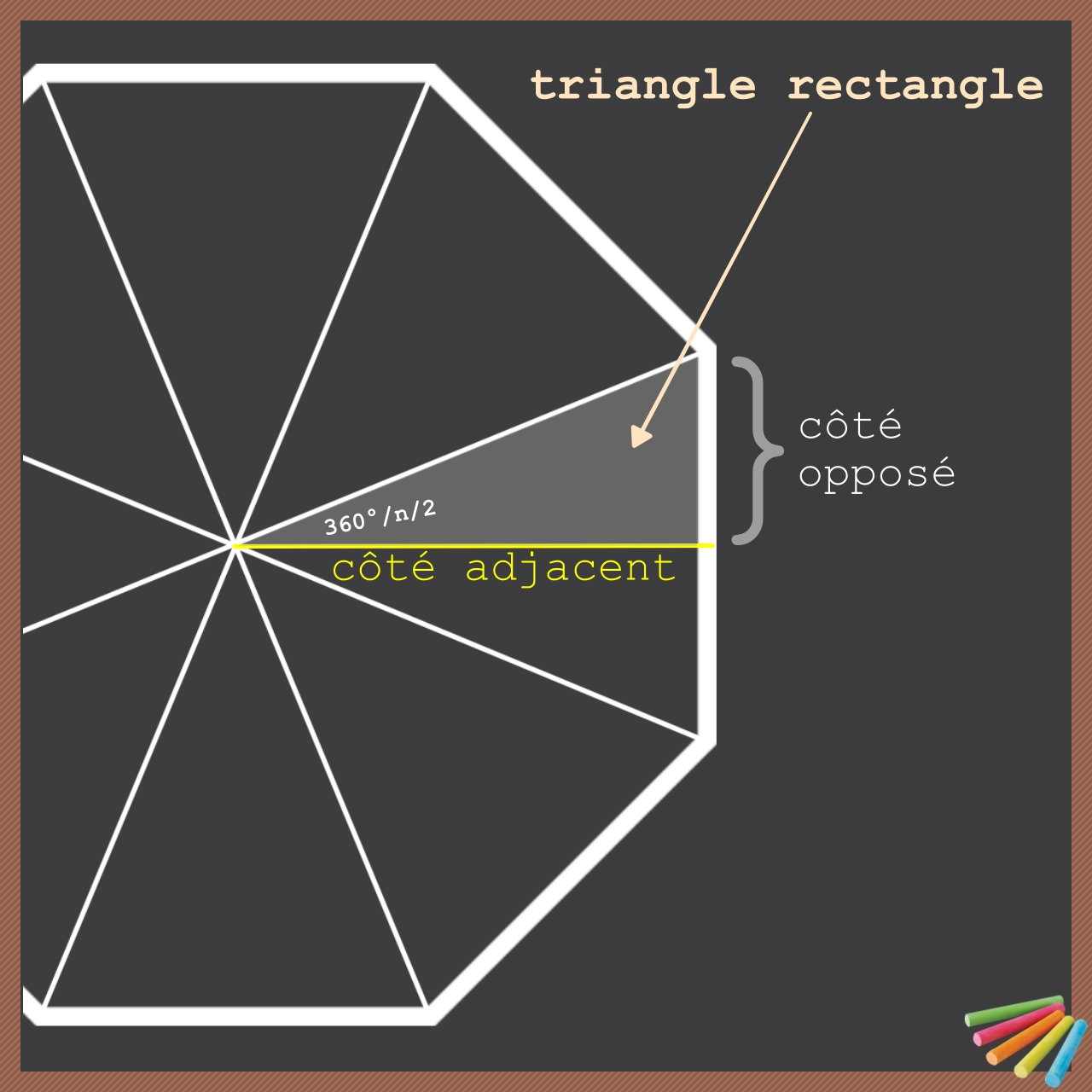
Un triangle isocèle se divise en 2 triangles rectangles par la hauteur élevée depuis sa base (vers le sommet).
Note: la hauteur depuis la base d'un triangle isocèle est également sa médiane et sa bissectrice et constitue aussi son axe de symétrie.
En conséquence, un polygone régulier et convexe sera constitué d'un ensemble (*) de triangles rectangles identiques.
(*) le nombre de triangles rectangles est égal au nombre de côtés du polygone multiplié par 2. Ainsi, un octogone sera constitué de 16 (2 x 8) triangles rectangles identiques.
Il est donc aisé de comprendre que l'aire d'un polygone régulier et convexe est l'aire d'un triangle rectangle multiplié par le double du nombre de côtés de ce polygone.
Connaissant le périmètre et le nombre de côtés, la dimension d'un côté est évidente (on divise, bien-sûr, le périmètre par le nombre de côtés).
Connaissant le nombre de côtés, il est également aisé de connaître l'angle du sommet des triangles isocèles (angles qui "pointent" vers le centre du polygone):
- pour un hexagone: 60° (360°/6),
- pour un octogone: 45° (360°/8),
- pour un décagone: 36° (360°/10),
- etc ...
Pour calculer l'aire d'un polygone régulier et convexe avec comme données le nombre de côtés, la dimension du côté et l'angle au sommet du triangle isocèle, il va falloir utiliser la trigonométrie (voir planche 3)
Soit un octogone dont le périmètre est 64 (mètres, par exemple), quelle est sa surface?
L'aire d'un triangle rectangle est égale à la moitié du produit des deux côtés formant l'angle droit.
La moitié du côté du polygone est la dimension de l'un des côtés de l'angle droit du triangle rectangle.
• soit 64/8/2 = 4
L'angle est la moitié de l'angle au sommet du triangle isocèle:
• soit 360°/8/2 = 22,5°
Sachant que la tangente d'un angle est égale au côté opposé divisé par le côté adjacent, on peut calculer l'autre côté de l'angle droit du triangle rectangle:
Note (rappel): dans un triangle ABC rectangle en C (voir ci-dessous) la tangente de l'angle B est le rapport entre le côté opposé et le côté adjacent. Il sera donc aisé de calculer la dimension du côté adjacent connaissant la valeur de l'angle B et la dimension du côté opposé.
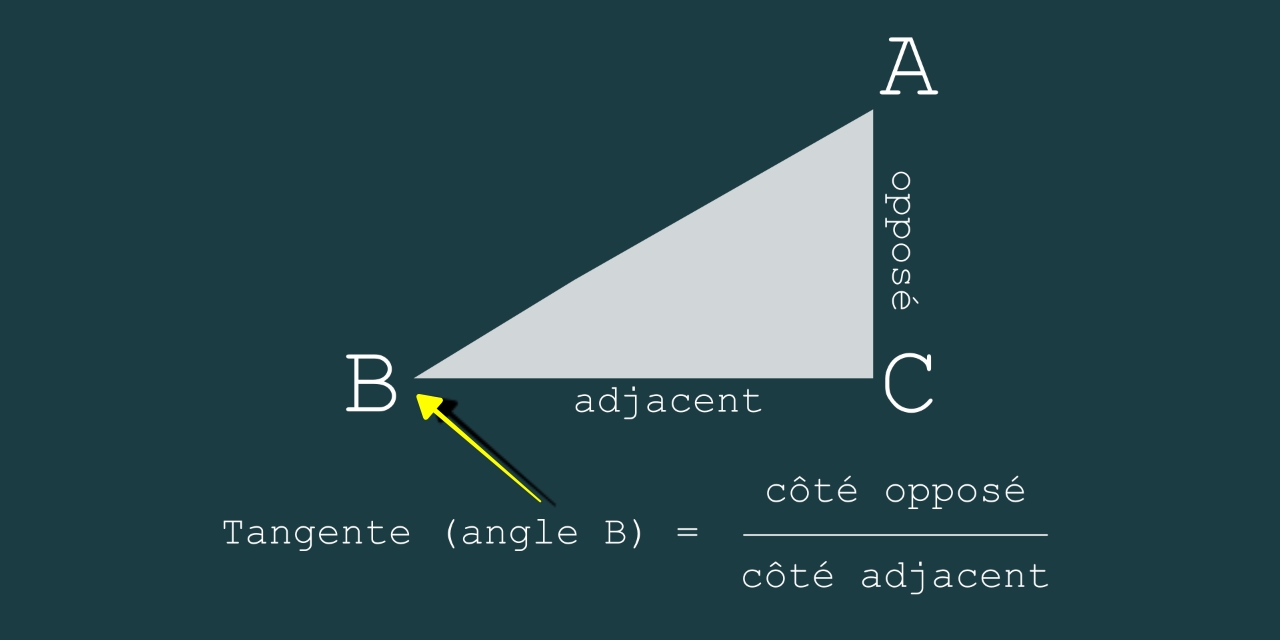
• soit Op le côté opposé (= 4)
• soit Ad le côté adjacent (= ?)
• donc Tangente(22,5°) = 4/Ad
• donc Ad = 4/Tangente(22,5°)
• donc Ad = 4/0,4142 = 9,6571
La surface S du triangle rectangle peut maintenant être calculée:
• soit S = (4*9,6571)/2 = 19,3142
La surface de l'octogone est 16 fois la surface du triangle rectangle:
• soit 19,3142*16 = 309,02 (m²)

Éléments connus:
• périmètre: P
• nombre de côtés: n
Calcul de la surface S:


• • •
• •
•
• •
•
