
les
nombres premiers
dans
l'univers des
mathématiques
nombres premiers
dans
l'univers des
mathématiques

Dans cette page sont abordés:
• la définition,
• le théorème fondamental,
• le crible d'Ératosthène,
• les nombres premiers entre eux,
• les triplets pythagoriciens,
• ...
• ...

1) définition
Un nombre premier est un entier naturel (et positif) qui n'admet que 2 diviseurs entiers (et positifs): 1 et lui-même.
Il y a, par exemple, 168 nombres premiers entre 1 et 1000 (voir la liste ci-dessous).
Premier constat: 2 est l'unique nombre premier pair.


2) théorème fondamental
Tout entier strictement positif peut être écrit comme un produit de nombres premiers d'une unique façon:
(NP signifie Nombre Premier)
• 33 = 3 * 11
3 et 11 sont des NP
• 48 = 2 * 2 * 2 * 2 * 3
• 48 = 2^4 * 3
2 et 3 sont des NP
• 150 = 2 * 3 * 5^2
2, 3 et 5 sont des NP
• 400 = 2^4 * 5^2
2 et 5 sont des NP
• 402 = 2 * 3 * 67
2, 3 et 67 sont des NP
• 2019 = 3 * 673
3 et 673 sont des NP
• 6051 = 3 * 2017
3 et 2017 sont des NP
• etc.
C'est le théorème fondamental de l'arithmétique (ou théorème de décomposition en produit de facteurs premiers).

3) le crible d'Ératosthène
Le crible d'Ératosthène est une algorithme (suite d’opérations ou d'instructions qui permettent de résoudre un problème) qui consiste à supprimer d'une table d'entiers de 1 à n tous les multiples d'un entier jusqu'à la racine carrée de n et de révéler ainsi les nombres premiers entre 1 et n.
Démonstration par l'exemple ci-dessous (en 4 images):
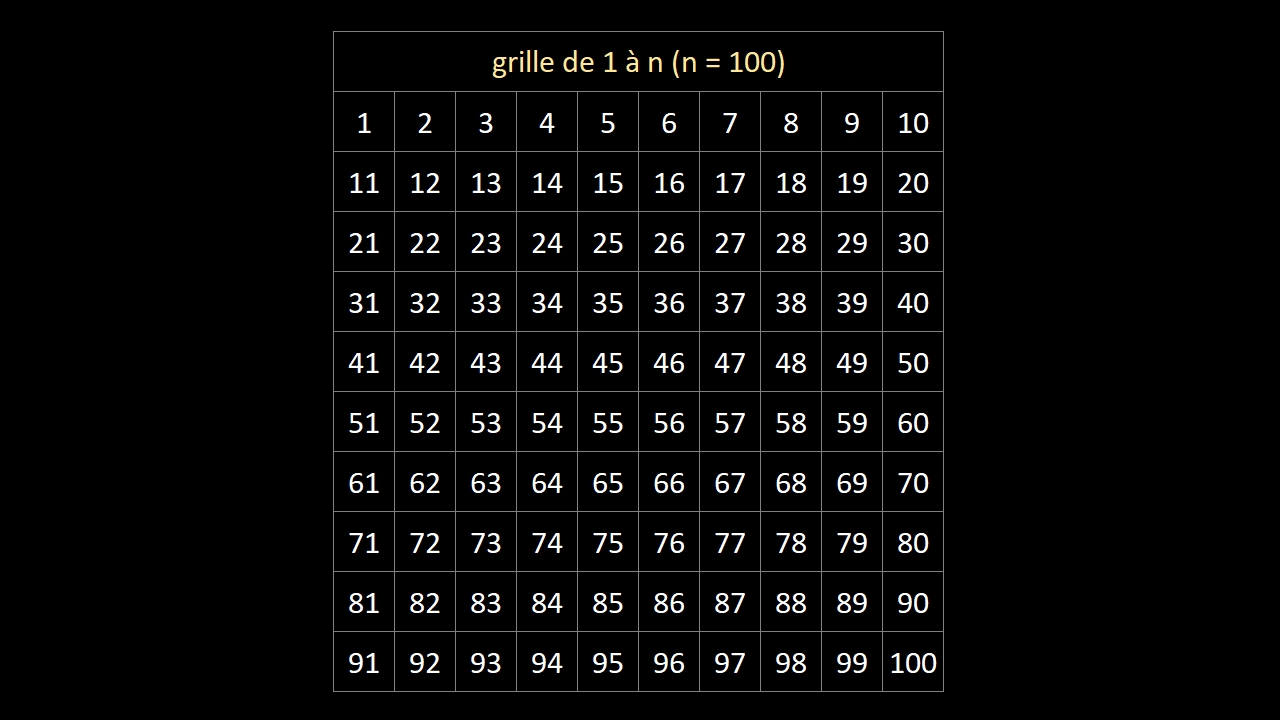


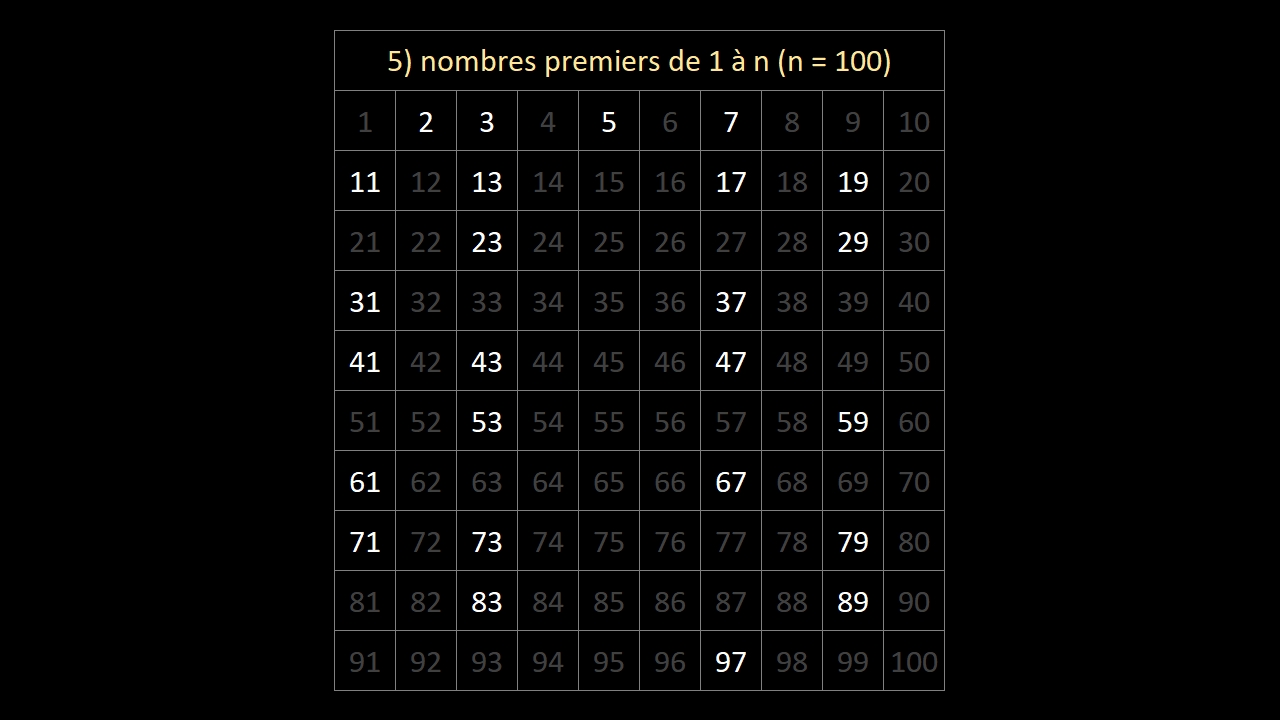
Comme la racine carrée de 100 est 10 (borne n de la table) le processus s'est arrêté car l'entier 11, qui devait être le critère d'analyse, est supérieur à 10.
En conséquence, la figure ci-dessus est, au terme de l'algorithme, la table qui présente tous les nombres entiers entre 1 et n (n = 100).
Note: entre 1 et 100, il y a 25 nombres premiers.

4) les nombres premiers entre eux
Deux nombres non premiers, peuvent l'être entre eux s'ils n'ont aucun diviseur commun à l'exception de 1. Exemple:
• 28 = 1 * 2^2 * 7
donc les diviseurs sont 1, 2 et 7
• 45 = 1 * 3 * 5^2
donc les diviseurs sont 1, 3 et 5
On constate que 28 et 45 ne sont pas des nombres premiers mais comme ces deux nombres n'ont que 1 comme diviseur commun, ILS SONT PREMIERS ENTRE EUX.
Ci-dessous, deux autres exemples de nombres non premiers mais premiers entre eux:
• 65 = 1 * 5 * 13
donc les diviseurs sont 1, 5 et 13
• 72 = 1 * 2^3 * 3^3
donc les diviseurs sont 1, 2 et 9
Les nombres 65 et 72 (non premiers) sont premiers entre eux car 1 est le seul diviseur commun entre ces deux nombres.
5) les triplets pythagoriciens
Il y a même des cas où trois nombres peuvent être premiers entre eux. Par exemple:
• 36 = 1 * 2^2 * 3^2
donc les diviseurs sont 1, 2 et 3
• 77 = 1 * 7 * 11
donc les diviseurs sont 1, 7 et 11
• 85 = 1 * 5 * 17
donc les diviseurs sont 1, 5 et 17
Les nombres 36, 77 et 85 (non premiers) sont premiers entre eux car 1 est le seul diviseur commun entre ces trois nombres.
Dans quel domaine, par exemple, peut-on trouver intéressant d'associer trois nombres premiers entre eux?
Dans le domaine de la trigonométrie et plus précisemment dans les triangles rectangles en appliquant le théorème de Pythagore:
Dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Voir l'image ci-dessous où la somme des carrés des côtés adjacents à l'angle droit (9 + 16) est égale au carré de l'hypoténuse (25) pour un triangle dont les côtés sont donc 3, 4 et 5 (hypoténuse):

Quand les longueurs des trois côtés d'un triangle rectangle sont des nombres entiers et premiers entre eux on dit que ce triangle est un TRIPLET PYTHAGORICIEN PRIMITIF.
Exemple avec les trois nombres 36, 77 et 85 qui sont premiers entre eux (voir plus haut):
• 36^2 + 77^2 = 85^2
• 1296 + 5929 = 7225
Un triangle dont les trois côtés sont 3, 4 et 5 est également un triplet pythagoricien primitif, tout comme avec 9, 10 et 41 (ou avec 33, 56 et 65).
Un triangle dont les trois côtés sont 6, 8 et 10 est également un triplet pythagoricien mais pas primitif car les valeurs des trois côtés ne sont pas des nombre premiers entre eux.

6) constats
En observant bien les 10 images ci-dessous (les 168 nombres premiers entre 1 et 1000) ...
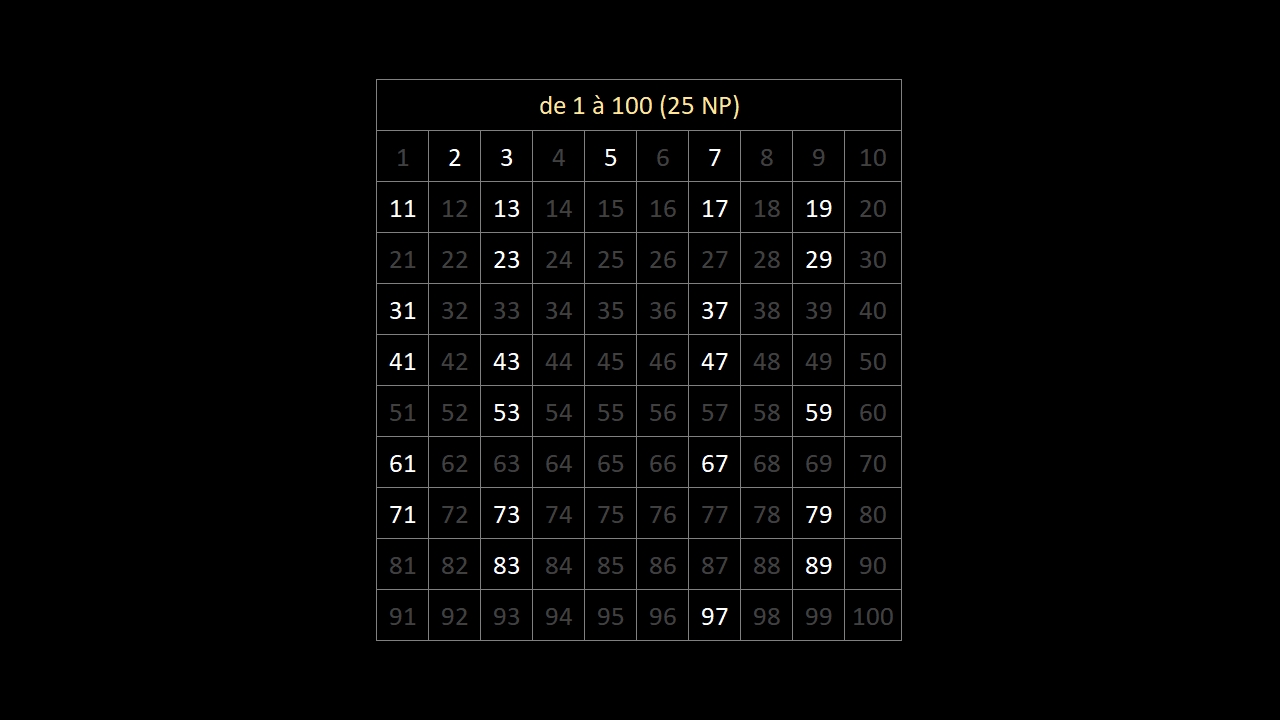
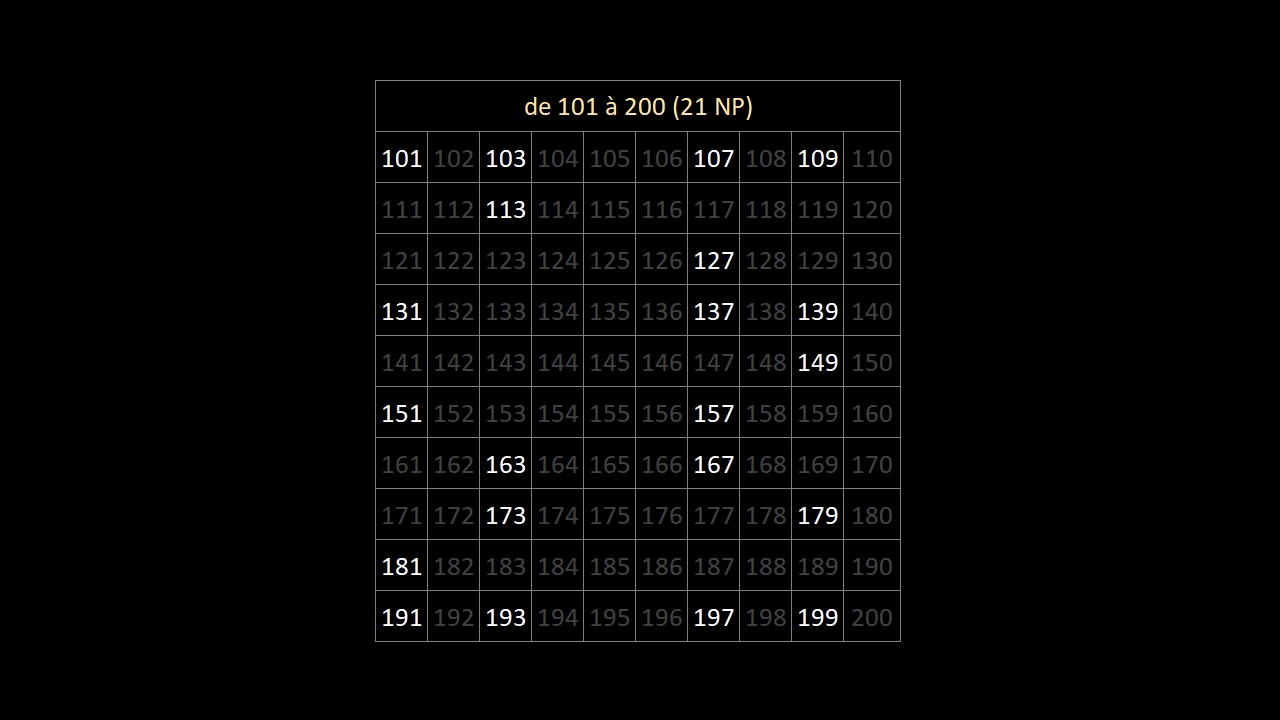
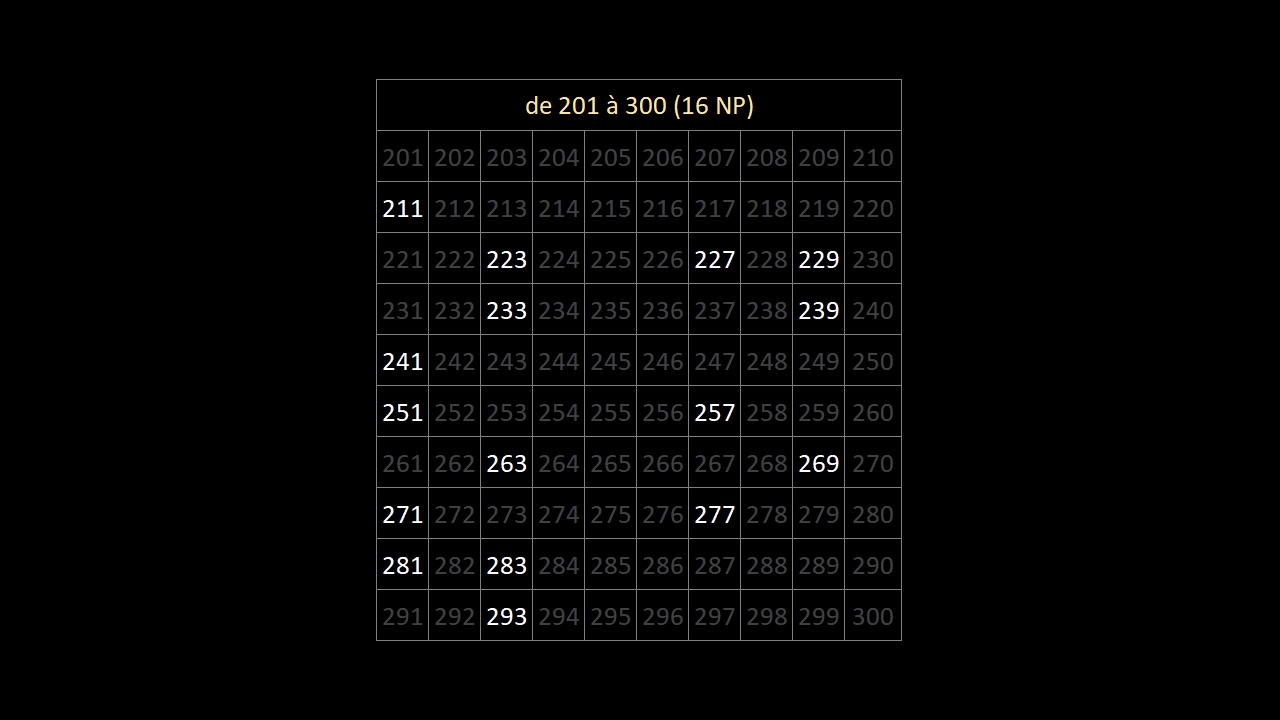
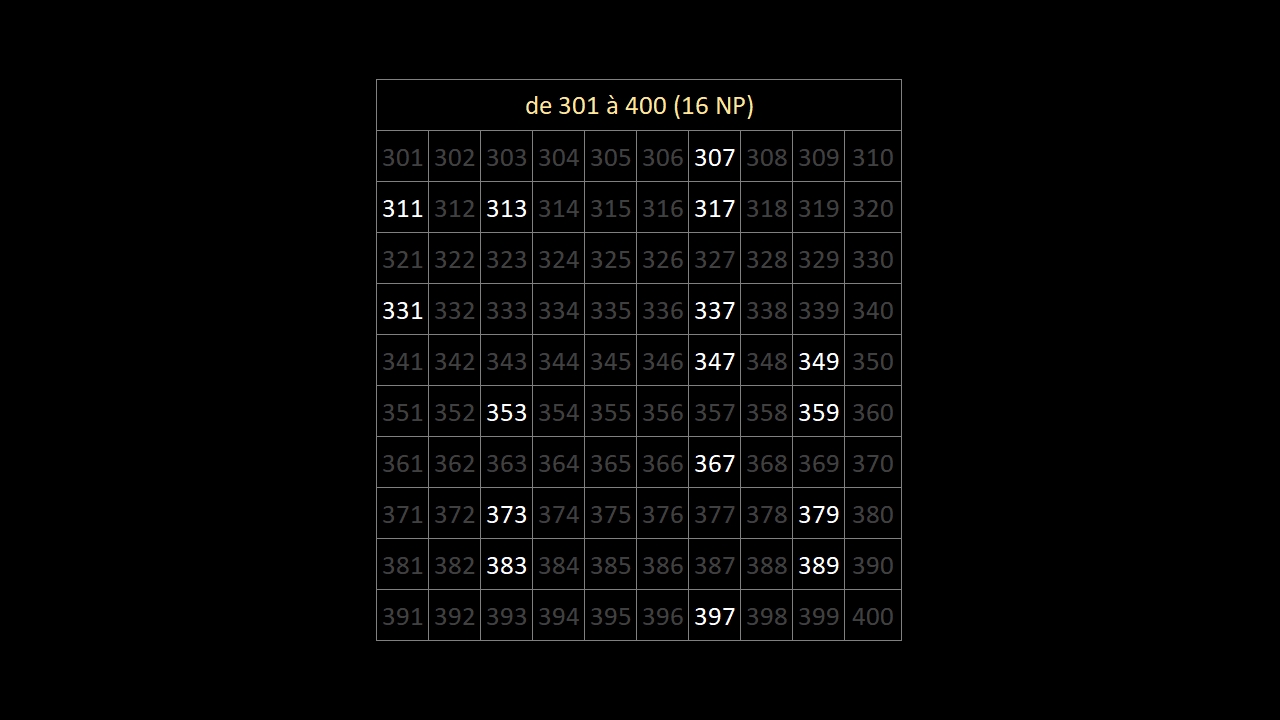
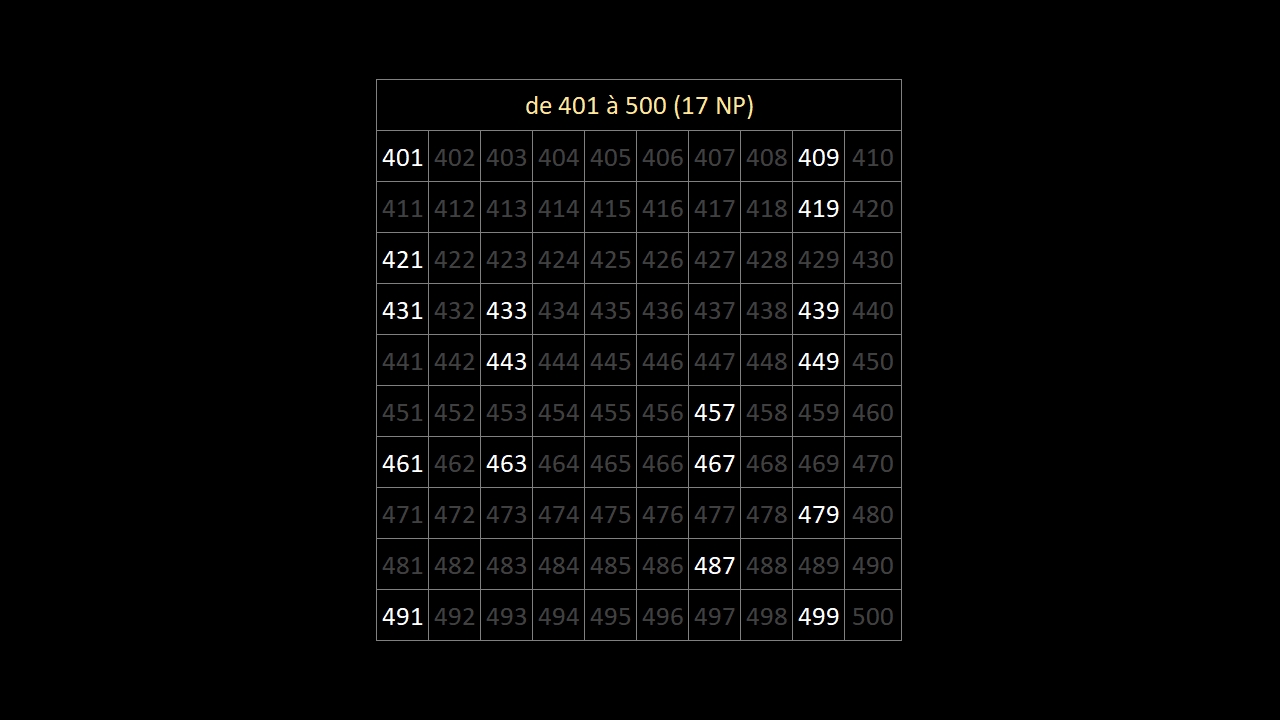
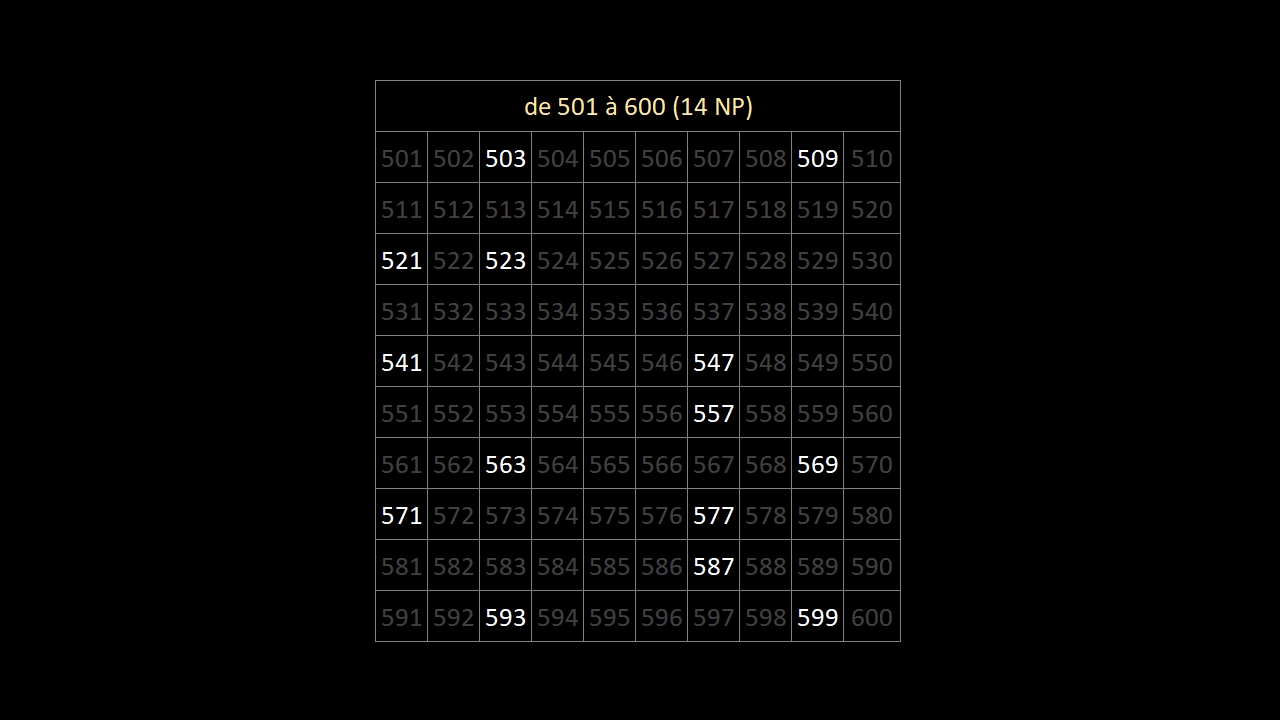
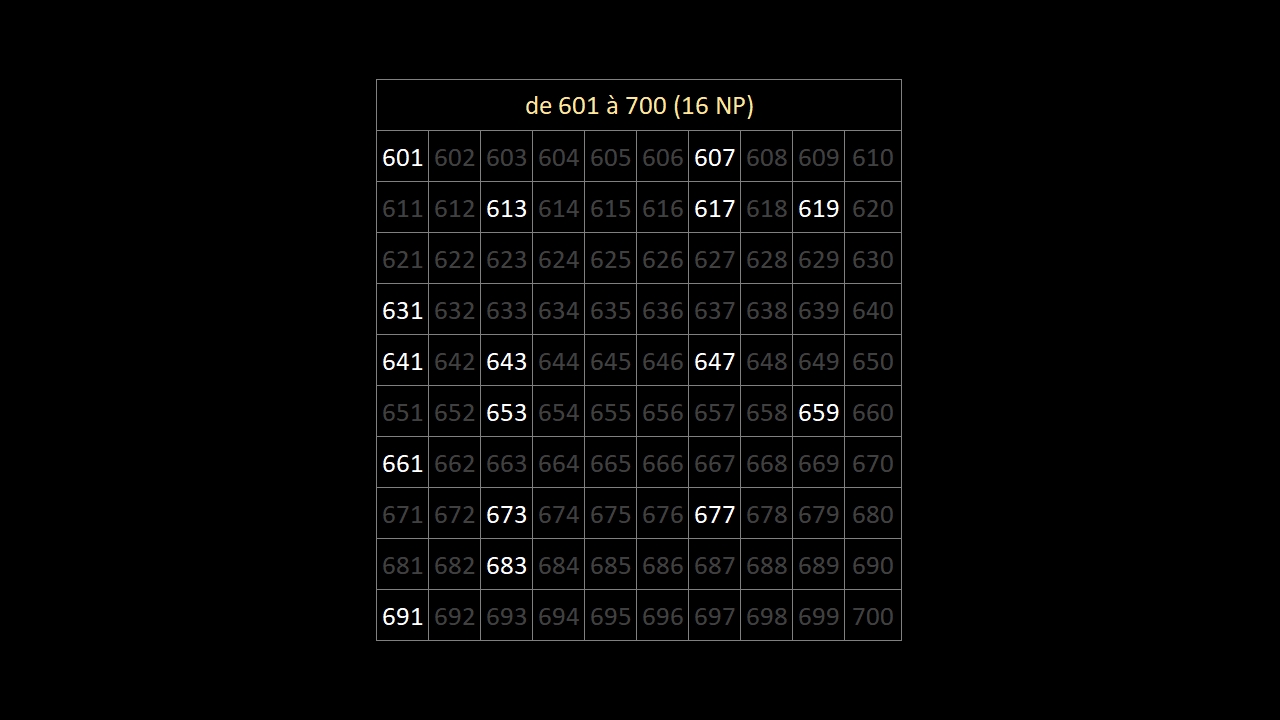
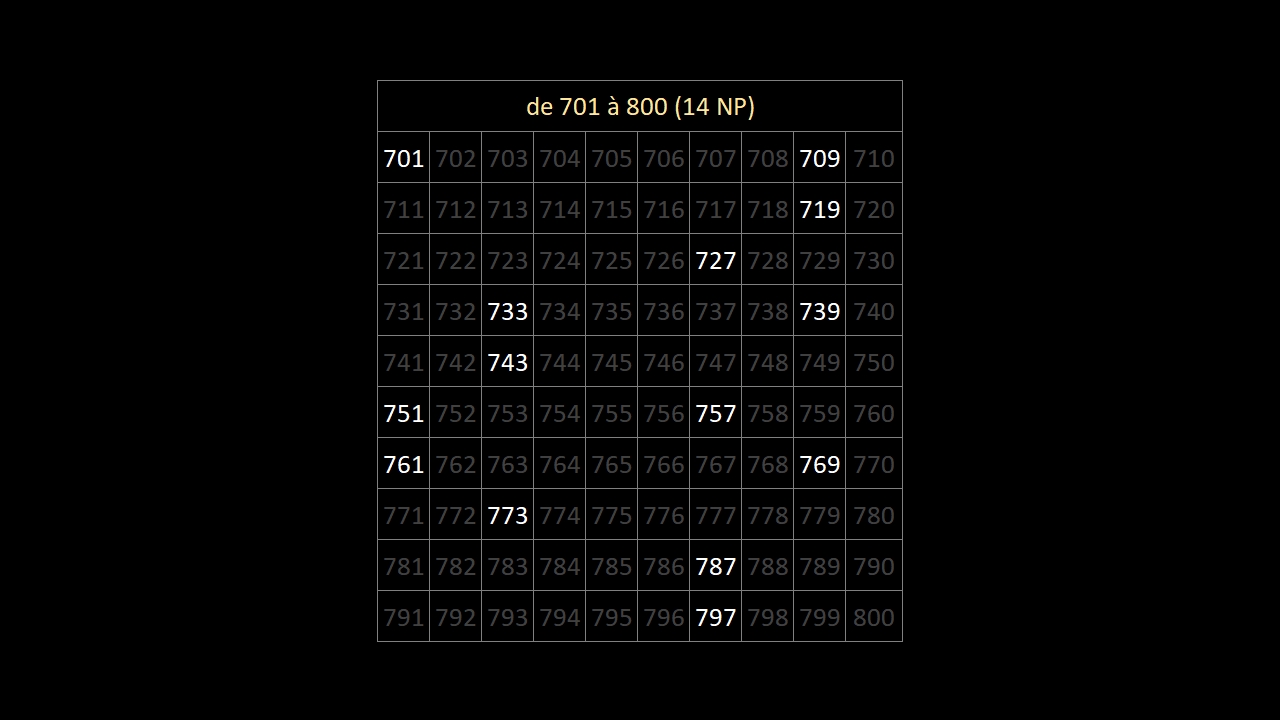
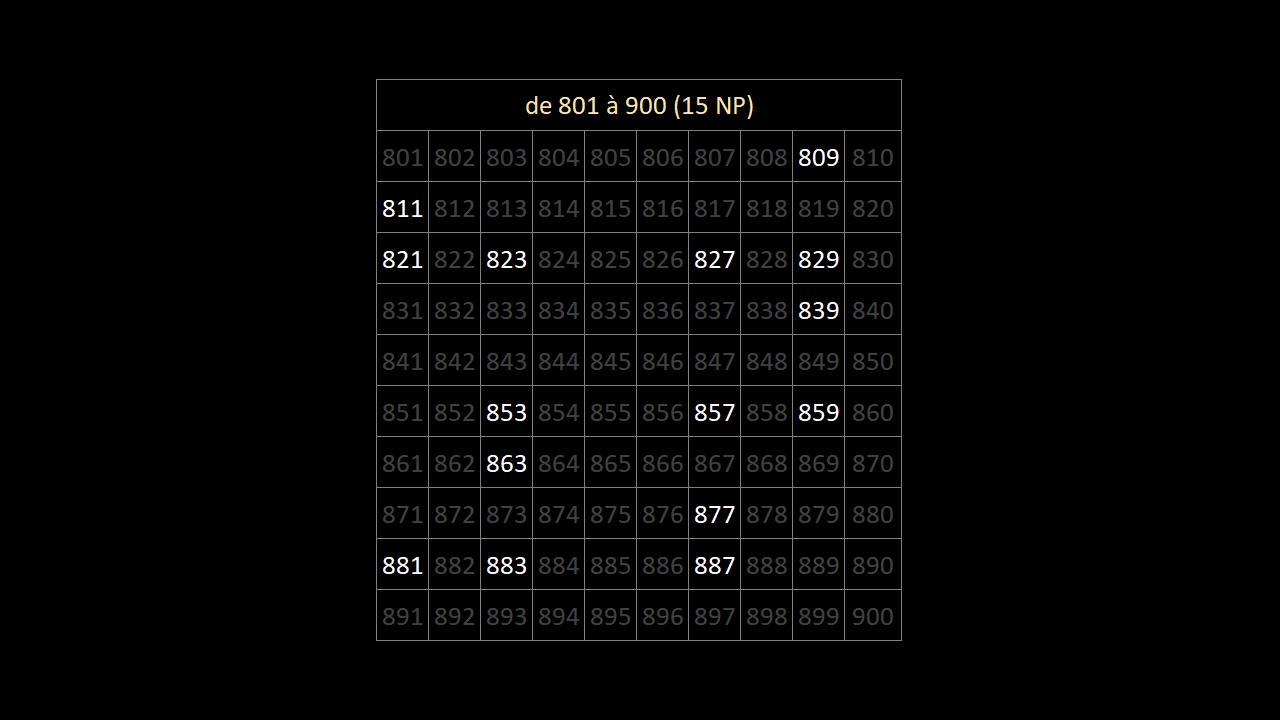
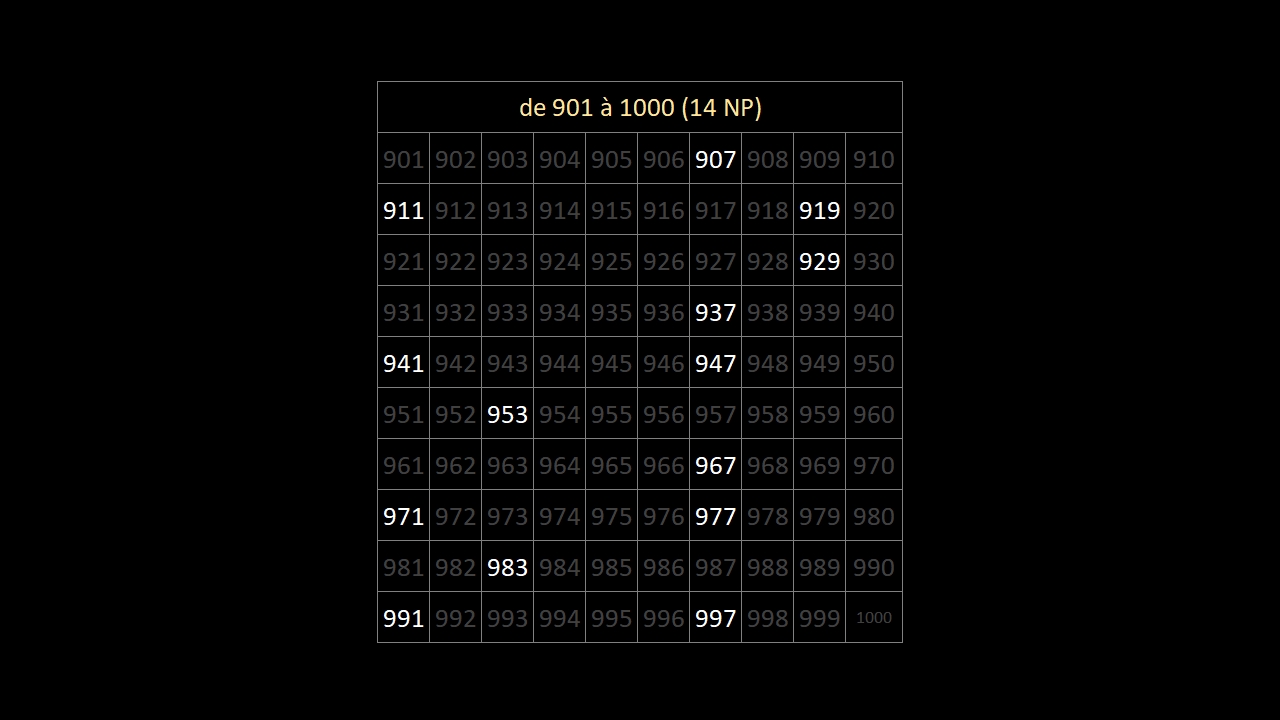
... on constate qu'au-delà du nombre premier 5, les nombres premiers finissent:
• toujours par 1, 3, 7 ou 9
• jamais par 2, 4, 5, 6, 8 ou 0
... ce qui est logique pour les terminaisons paires (2, 4, 6, 8 et 0). Quant aux terminaisons impaires, on notera que tous les nombres dont l'unité est 5 sont divisibles par 5.
Note: ce qui est vrai pour les nombres premiers entre 1 et 1000 est vrai pour tous les nombres premiers.
Question:

(*) sauf le nombre premier 2

• • •
• •
•
• •
•
