la
somme
des carrés
des n premiers
nombres entiers
somme
des carrés
des n premiers
nombres entiers
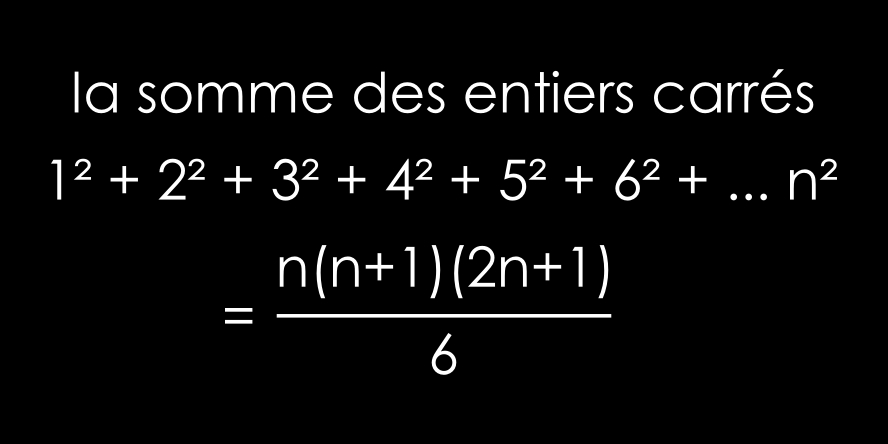
Démonstration
en 7 étapes avec des cubes!
en 7 étapes avec des cubes!

étape 1
Soit S = 1² + 2² + 3² + 4² (= 30)1² --> 1 cube blanc
2² --> 4 cubes bleus
3² --> 9 cubes oranges
4² --> 16 cubes gris
... soit 30 cubes au total.

étape 2
Disposons les 30 cubes de telle façon que la base soit formée de 4 sur 5 cubes.

étape 3
Disposons par-dessus un même lot de 30 cubes ...

étape 4
... on obtient ainsi un bloc de 2 fois 30 cubes, soit 60 cubes.

étape 5
Ajoutons un troisième lot (le dernier) de 30 cubes. On obtient donc 90 cubes.

étape 6
Répartissons les 10 cubes du dessus en 20 demi-cubes pour niveler le haut et obtenir ainsi une forme globale bien parallélépipédique.
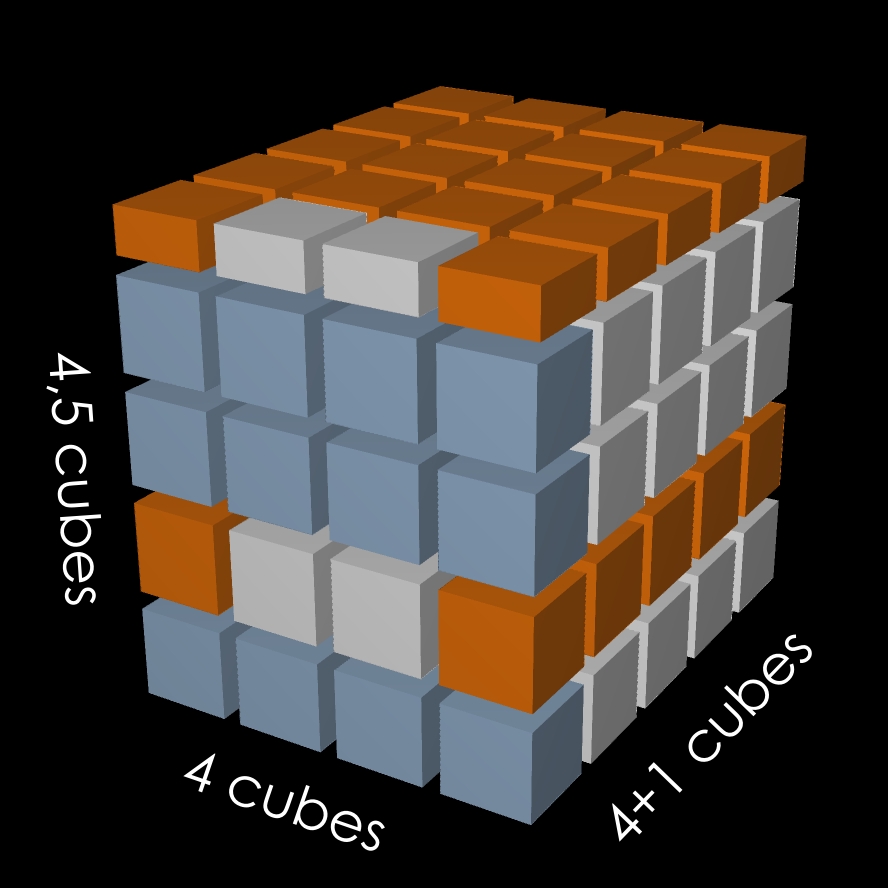
étape 7
Nous pouvons donc écrire en observant le volume du bloc formé par les 3 lots de 30 cubes avec 4 cubes en largeur, 4+1 cubes en longueur et 4+1/2 cubes en hauteur:
3*S = 90
ou
3*(1²+2²+3²+4²) = 4*(4+1)*(4+1/2)
ou
3*(1²+2²+3²+4²) = 4*(4+1)*(4+1/2)
Remplaçons 4 par n:
S = 1² + 2² + .. + n²
3*(1²+2²+..+n²) = n*(n+1)*(n+1/2)
Simplifions:
3*(1²+2²+..+n²) = n*(n+1)*(n+1/2)
6*(1²+2²+..+n²) = n*(n+1)*(n+1/2)*2
6*(1²+2²+..+n²) = n*(n+1)*(2n+1)
1²+2²+..+n² = (n*(n+1)*(2n+1))/6
n*(n+1)*(2n+1)
S = --------------
6
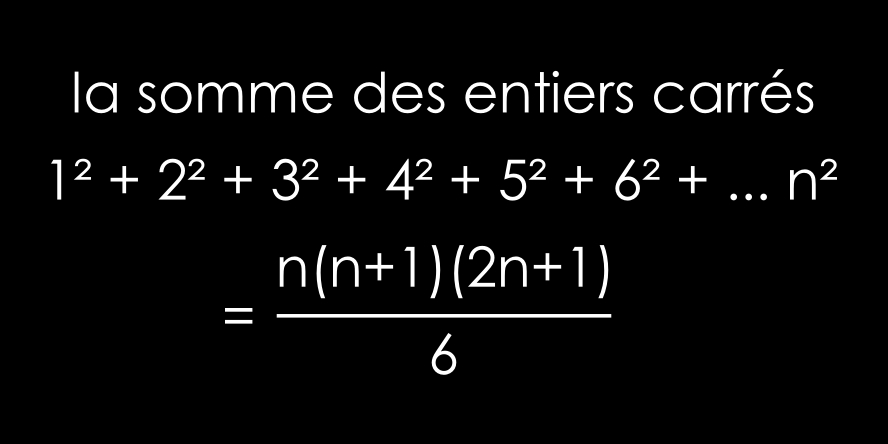
Exemple avec n = 10:
1² + 2² + 3² + 4² + 5² + 6² + 7² + 8² + 9² + 10² = 1 + 4 + 9 + 16 + 25 + 36 + 49 + 64 + 81 + 100 = 385
(10*(10+1)*(2*10+1))/6 = 2310/6 = 385
Exemple avec n = 17:
1² + 2² + 3² + 4² + 5² + 6² + 7² + 8² + 9² + 10² + 11² + 12² + 13² + 14² + 15² + 16² + 17² = 1 + 4 + 9 + 16 + 25 + 36 + 49 + 64 + 81 + 100 + 121 + 144 + 169 + 196 + 225 + 256 + 289 = 1785
(17*(17+1)*(2*17+1))/6 = 1785
Exemple avec n = 100:
(100*(100+1)*(2*100+1))/6 = 338350
Exemple avec n = 512:
(512*(512+1)*(2*512+1))/6 = 44870400
Commentaires (et conclusion)
Cette démonstration (assez proche de "la méthode de Singapour") fonctionne avec un total de cubes divisible par 3. Ainsi, avec n = 13, le nombre total de cubes aurait été 819 qui peut se diviser en 3 lots de 273 cubes chacun.
Il en aurait été de même avec n = 27. Le nombre total de cubes aurait été alors de 6930 cubes, ce qui représente 3 lots de 2310 cubes chacun.
Cette page est inspirée (pas recopiée) de démonstrations que j'ai découvertes sur Internet (YouTube). Ces démon-strations n'abordent pas un point fondamental qui est pourquoi elles reposent sur une répartition en 3 lots identiques (approche cubique). Point que je souhaiterais développer dans cette page.
