la
longueur
d'un
arc de cercle
longueur
d'un
arc de cercle
AVERTISSEMENT
Note: cette page a été développée essentiellement pour présenter, pas à pas, la méthode (assez complexe) qui permet de calculer la longueur d'un arc connaissant
seulement les longueurs de sa corde et de sa flèche (troisième cas, ci-dessous).
Cette page est consacrée aux arcs de cercle. Un arc de cercle est une partie de la circonférence d'un cercle. Lui sont donc associés, un rayon (le rayon de son cercle) et un angle (au centre de son cercle). On peut aisément calculer la longueur d'un arc en connaissant la longueur du rayon de son cercle et la valeur de l'angle de l'arc au centre de ce cercle. Mais on peut aussi déduire la taille du rayon et la valeur de l'angle à partir d'autres données comme, par exemple, les longueurs de la corde et de la hauteur (flèche) de l'arc.
CONTENU
• • •
• •
•
• •
•
premier cas
Calculer la longueur d'un arc de cercle à partir de son angle (en degrés) et du rayon de son cercle.

Soit un cercle ...
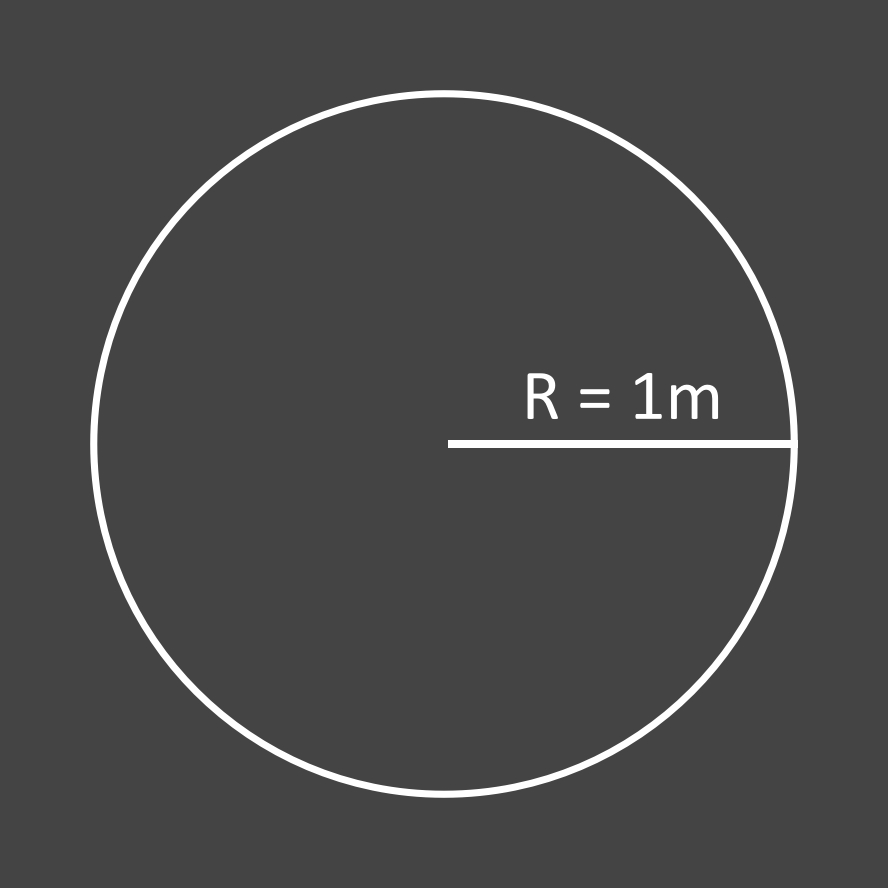
De rayon 1 (mètre) ...
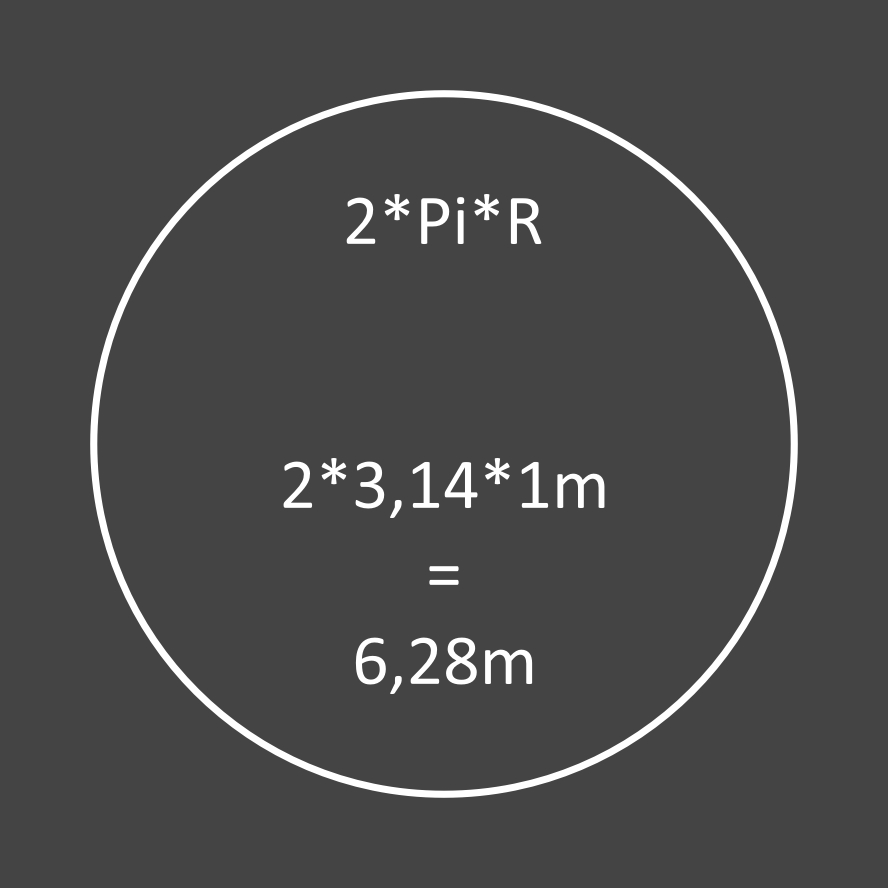
Circonférence = 6,28 mètres ...
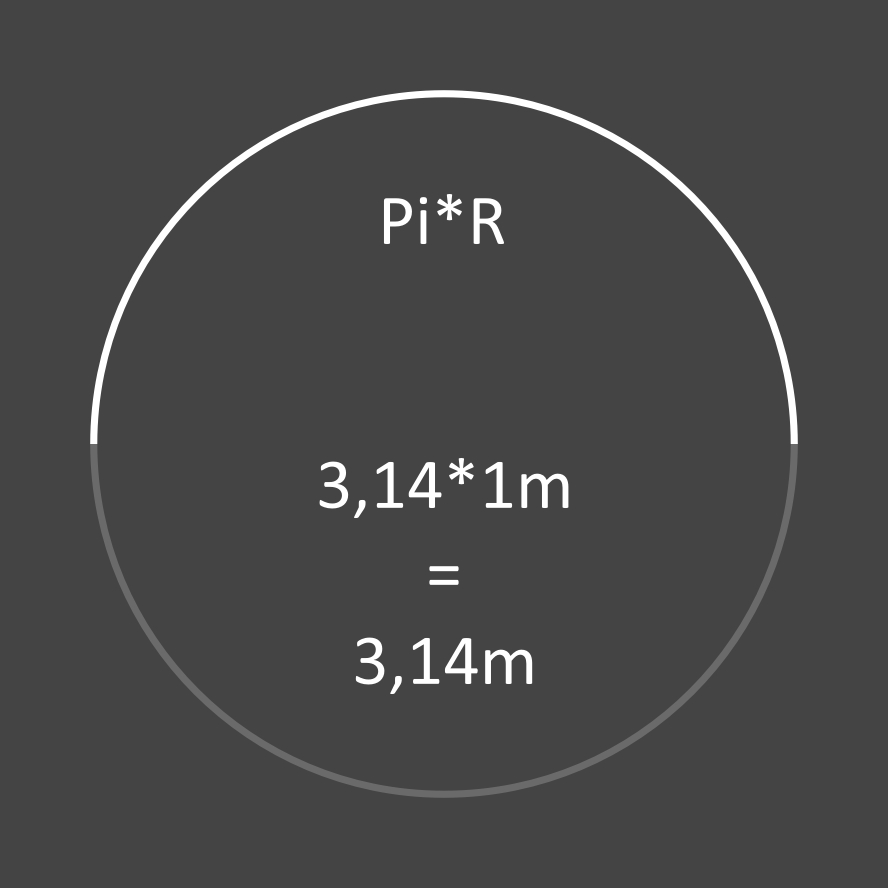
Demi-circonférence = 3,14 mètres ...
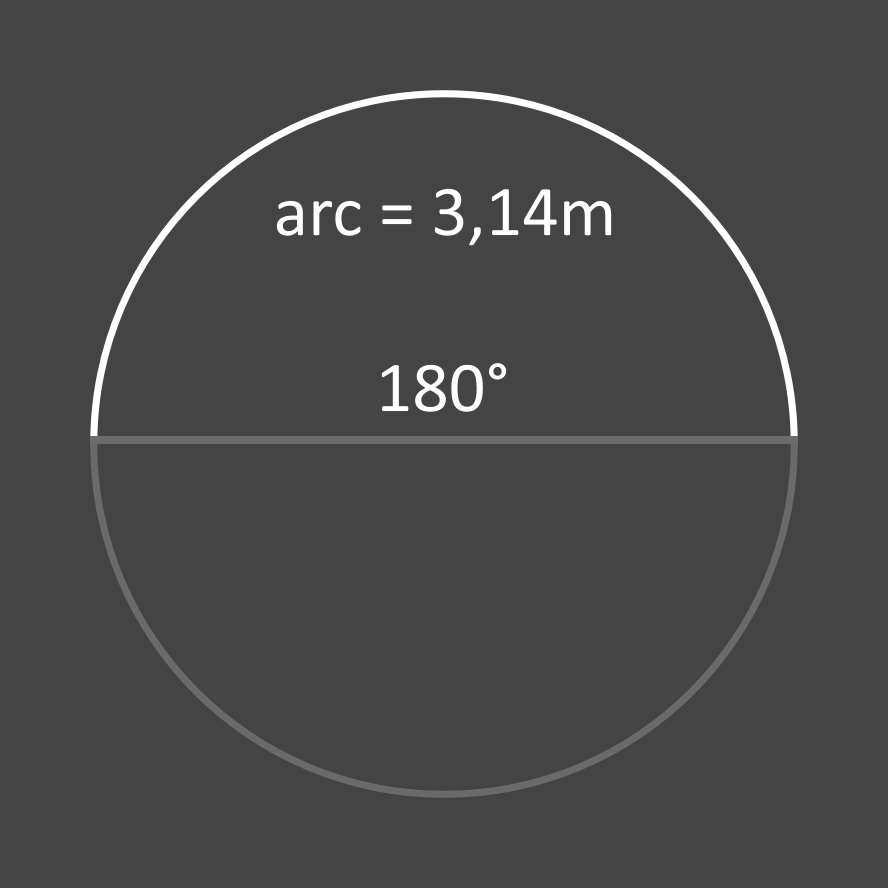
Conclusion 1:
la longueur d'un arc de 180° dans un cercle de rayon 1 est égale à Pi.
Conclusion 2:
la longueur d'un arc de 180° dans un cercle de rayon r est égale à Pi*r.
Conclusion 3:
la longueur d'un arc de a° dans un cercle de rayon r est égale à Pi*r/180*a.
Conclusion 4:
comme Pi/180 est égal à 0,01745, la longueur d'un arc de a° dans un cercle de rayon r est égale à 0,01745*r*a.
Formule retenue dans les livres:

• • •
• •
•
• •
•
deuxième cas
Calculer la longueur d'un arc de cercle à partir de la longueur de sa corde et du rayon de son cercle.
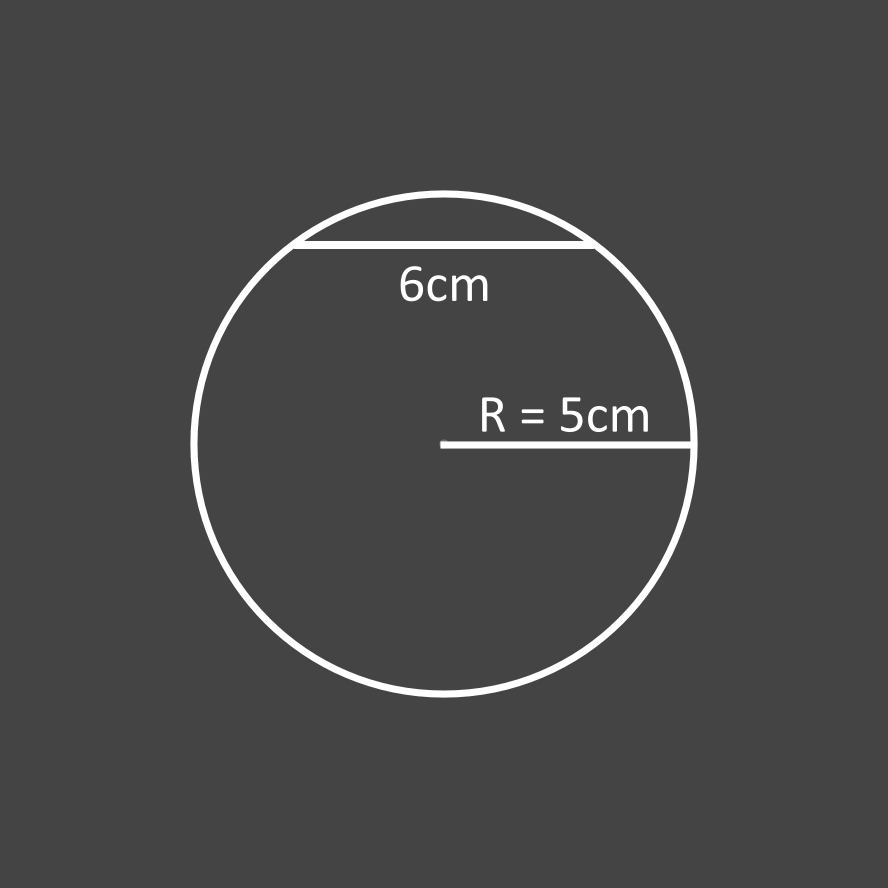
Peut-on calculer l'angle d'un arc (et en conséquence sa longueur) connaissant la longueur de sa corde et celle du rayon du cercle de l'arc?
Réponse: oui!
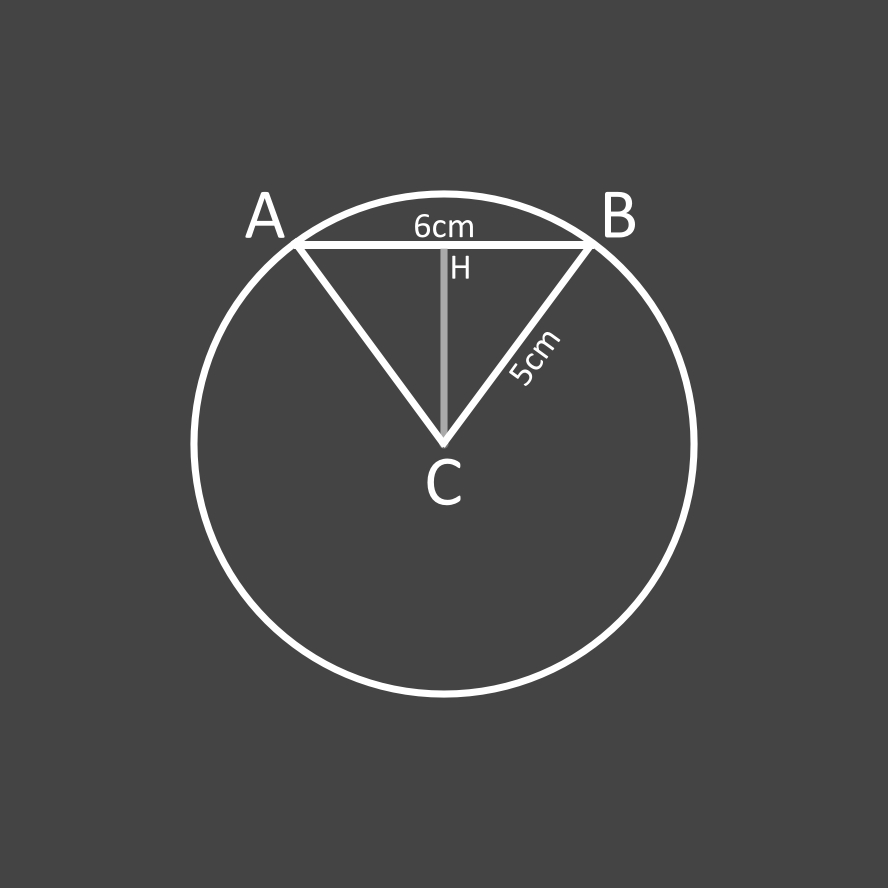
Sur le dessin ci-dessus apparaît un triangle isocèle (ABC) formé par deux rayons (AC et BC constituant les côtés égaux du triangle isocèle) et par la corde AB de l'arc (le troisième côté du triangle).
En portant dans le triangle isocèle une hauteur (CH) ayant comme base la corde (AB), on obtient deux triangles rectangles (HAC et HBC).
En considérant le triangle HBC (rectangle en H), on connaît la longueur de son hypoténuse (BC = rayon du cercle) ainsi que la longueur du côté HB (= la moitié de la corde AB).
Intervient alors un outil indispen-sable en mathématique: la trigo-nométrie.
Note: ce qui suit s'adresse à des personnes ayant des bases en trigo-nométrie.
On sait que le sinus de l'angle HCB est égal au rapport entre le côté opposé (HB) et l'hypoténuse (BC). HB étant au numérateur et BC au dénominateur.
On peut donc écrire:
sin(HCB) = HB/BC
Mais comme c'est la valeur de l'angle HCB que l'on cherche on peut donc écrire:
angle HCB = arcsin(HB/BC)
Exemple avec une corde de 6 cm d'un arc sur cercle de 5 cm de rayon:
• HB = AB/2 = 6/2 = 3
• BC = rayon = 5
• angle HCB = arcsin(HB/BC)
• angle HCB = arcsin(3/5) = 36,86°
• angle ACB = 36,86°*2 = 73,73°
Il ne reste plus qu'à appliquer la formule (voir plus haut dans cette page) pour calculer la longueur de l'arc ayant pour angle 73,73 degrés dans un cercle de rayon égal à 5 cm:
(Pi*r*a)/180
(Pi*5*73,73)/180 = 6,43 cm
Conclusion: un arc ayant une corde de 6 cm dans un cercle ayant un rayon de 5 cm fait une longueur de 6,43 cm.
(Pi*5*73,73)/180 = 6,43 cm
Et voici donc la formule:

• • •
• •
•
• •
•
troisième cas
Calculer la longueur d'un arc de cercle à partir de la longueur de sa corde et de sa flèche.
Note: "hauteur" ou "flèche" de l'arc s'emploient tous les deux pour désigner la même chose.
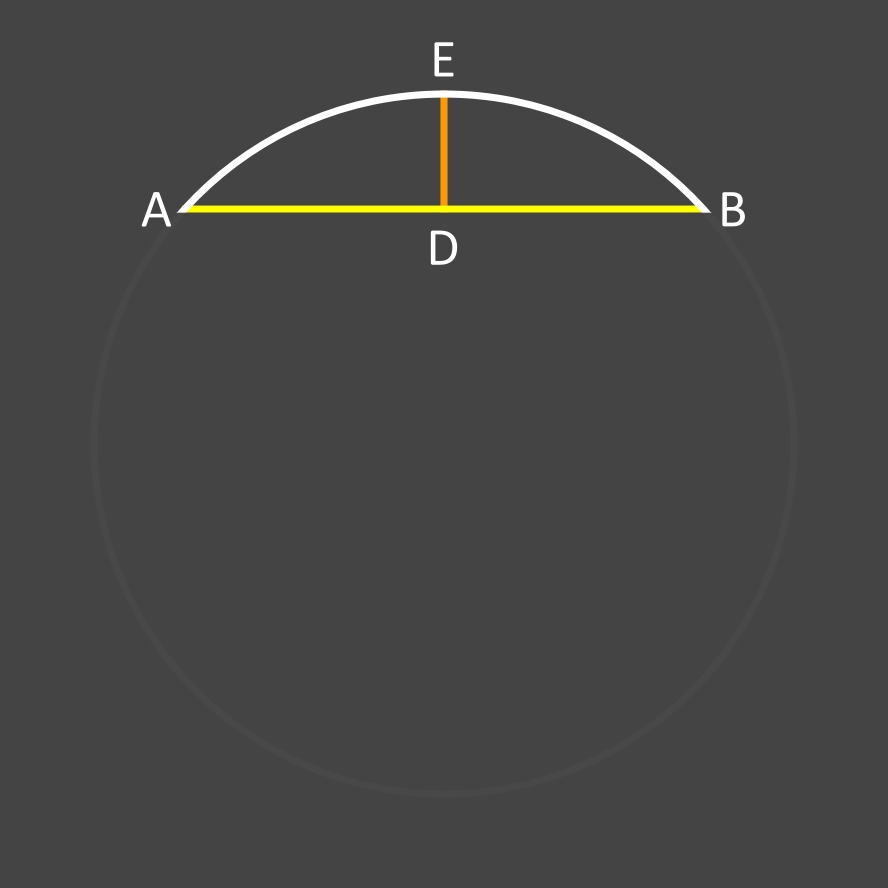
Peut-on calculer l'angle d'un arc et le rayon de son cercle connaissant la longueur de sa corde AB et celle de sa flèche DE, et rien d'autre (voir image ci-dessus)?
Réponse: oui!
La procédure se fera en deux étapes:
1) calcul de l'angle
2) calcul du rayon
1) calcul de l'angle
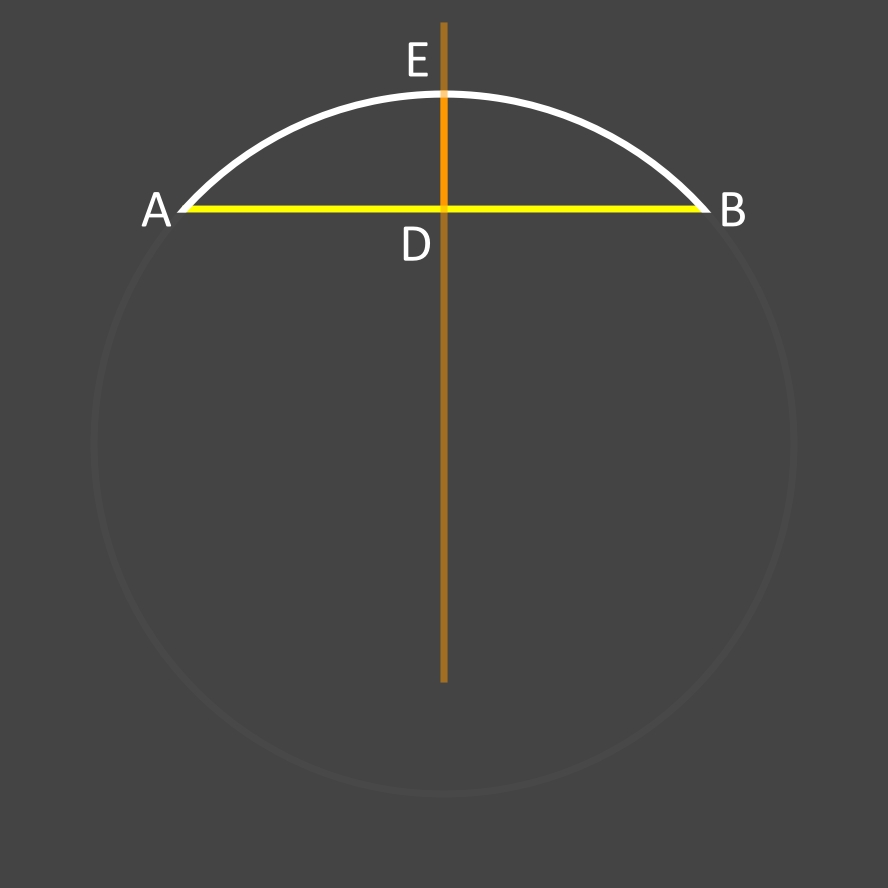
Porter, sur le dessin, une droite dans le prolongement de la flèche DE (trait orange) ...
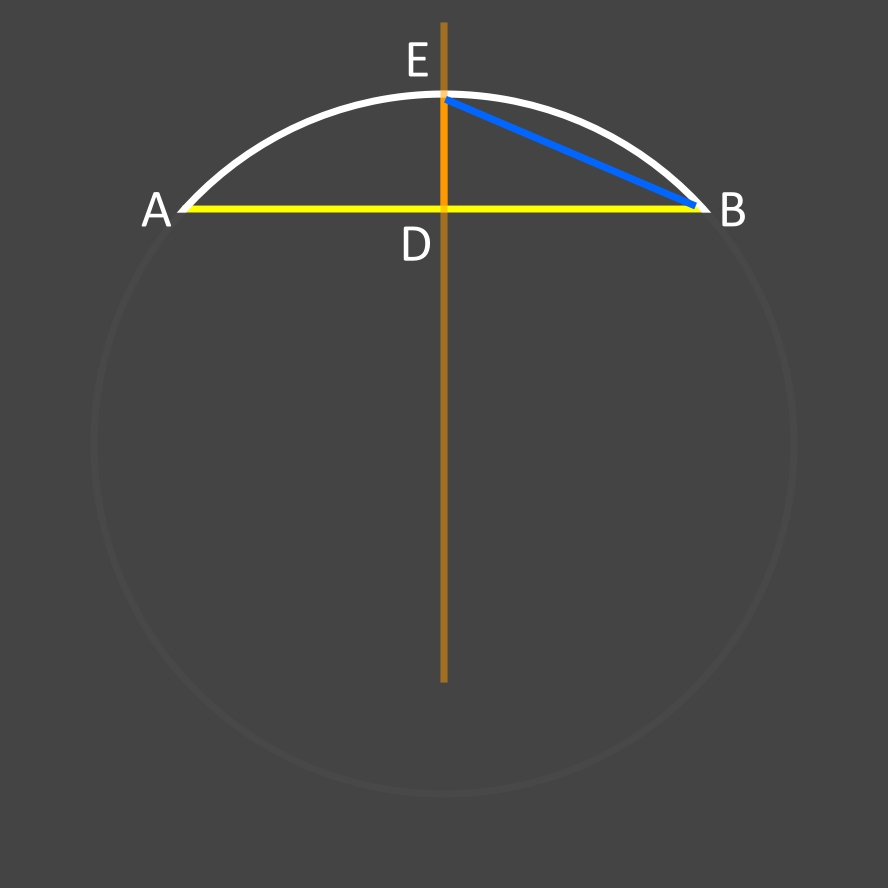
Relier les points E à B (trait bleu) ...
Il faut calculer EB. C'est simple car DEB est un triangle rectangle et que les valeurs DE et DB (AB/2) sont données dans l'hypothèse. EB étant l'hypoténuse du triangle rectangle on peut donc écrire en appliquant le théorème de Pythagore (note: "rac" signifie "racine carrée"):
• EB^2 = DE^2 + (AB/2)^2
• EB = rac(DE^2 + (AB/2)^2)
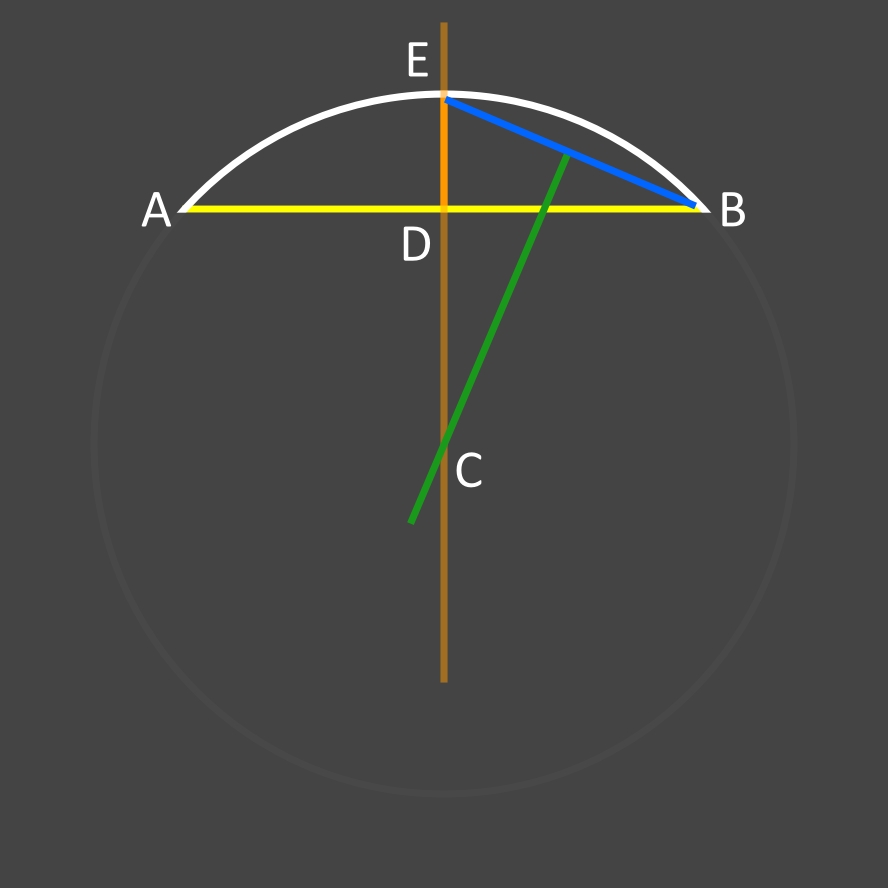
Tracer la médiatrice de DE (trait vert) qui ira couper le prolongement de la flèche (trait orange) à un point C ...
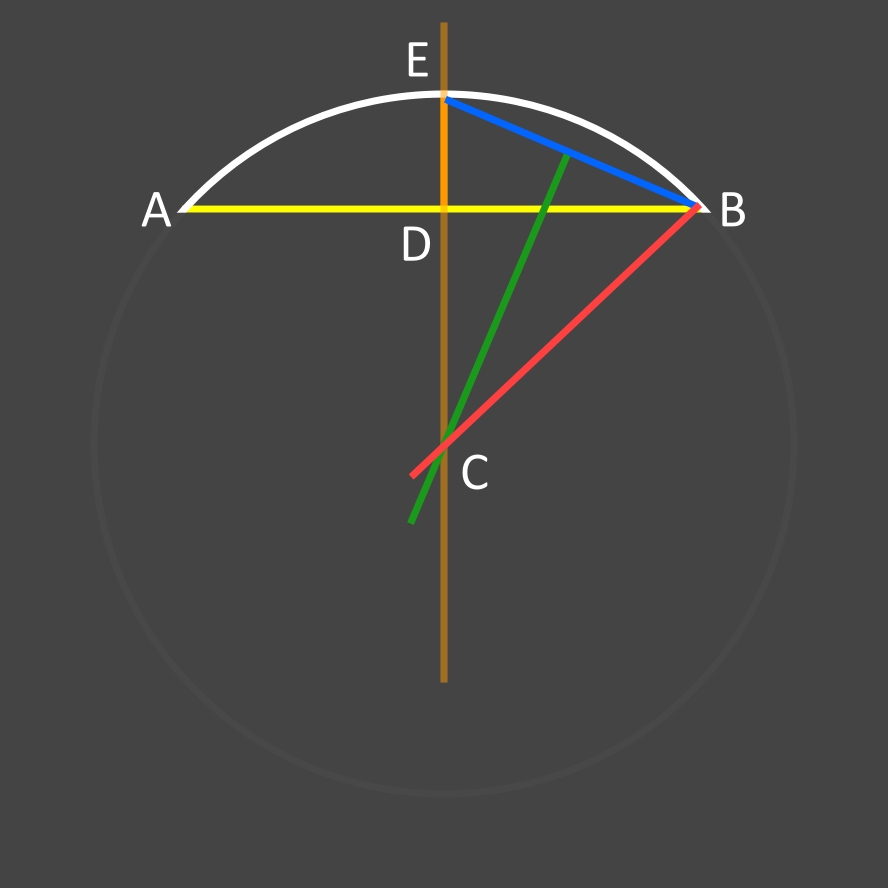
Relier B à C (trait rouge). Constat: le triangle EBC est un triangle isocèle et le point C est le centre du cercle de l'arc AB.
Il faut donc calculer l'angle DCB (que l'on multipliera par 2 pour connaître l'angle au cercle de l'arc AB).
L'angle DCB est égal à 180° moins 2 fois l'angle CEB (rappel: EBC est un triangle isocèle).
Les angles CEB et DEB ne font qu'un.
Connaissant les valeurs DB et DE, il sera aisé de calculer l'angle DEB, par la trigonométrie et, à partir de cet angle, caluler l'angle ECB:
• CEB = arcsin(DB/EB)
• ECB = 180° - 2*CEB
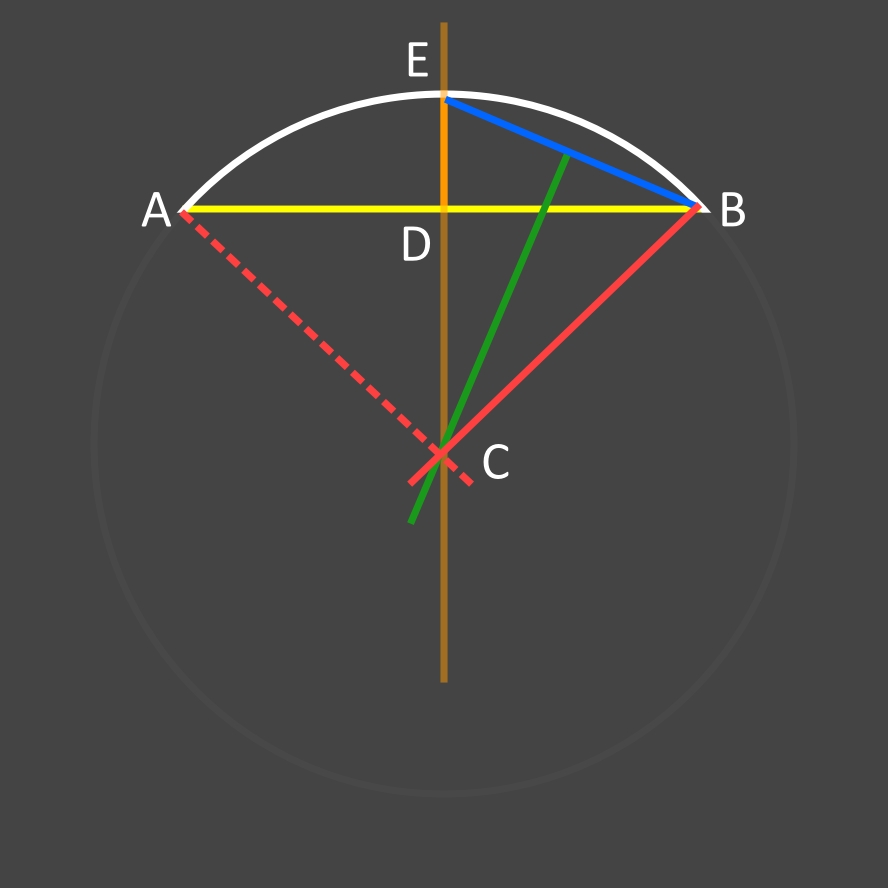
Il suffira de multiplier ECB par 2 pour connaître la valeur de l'angle au cercle (ACB) de l'arc AB et ainsi de pouvoir calculer sa longueur:
• angle ACB =
2*(180-2*(arcsin((AB/2)/(rac(DE^2+(AB/2)^2)))))
Conclusion (angle):
2*(180-2*(arcsin((AB/2)/(rac(DE^2+(AB/2)^2)))))
Le calcul de l'angle (a) d'un arc à partir de sa corde (c) et de sa flèche (f) peut être formulé de la façon suivante:

Exemple:
Quel est l'angle (en degrés) d'un arc AB sachant que sa corde est égale à 11 cm et que sa flèche DE est égale à 2 cm (voir image ci-dessus)?
Il faut tout d'abord calculer EB (hypoténuse du triangle rectangle DEB):
• EB = rac(2^2+(11/2)^2) = 5,85 cm
Il faut ensuite calculer (en degrés) l'angle CEB:
• CEB = arcsin((11/2)/5,85) = 70°
Ce qui permet de calculer l'angle ECB:
• ECB = 180 - (2*70) = 40°
Et d'obtenir la valeur de l'angle du cercle de l'arc AB:
• ACB = 2*40 = 80°
2) calcul du rayon
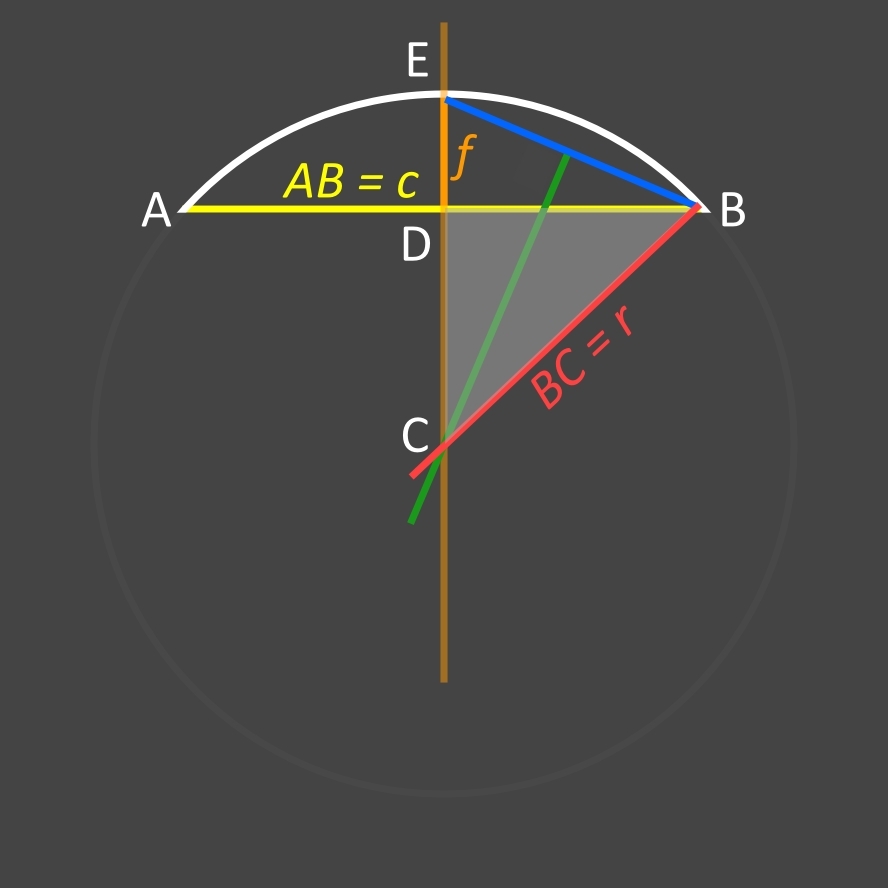
Il faut considérer le triangle rectangle CDB (en gris sur l'image ci-dessus):
• l'hypoténuse BC est le rayon et sera désigné par la lettre r
• le côté DB, qui est la moitié de la corde AB (lettre c), sera désigné par c/2
• le côté DC, qui est le rayon r moins la flèche DE (lettre f), sera désigné par r-f
On peut alors appliquer le théorème de Pythagore, puis développer:
• r^2 = (c/2)^2 + (r-f)^2
• r^2 = c^2/4 + r^2 - 2rf + f^2
• r^2 - r^2 = c^2/4 - 2rf + f^2
• 0 = c^2/4 - 2rf + f^2
• 2rf = c^2/4 + f^2
• r = (c^2/4 + f^2) /2f
• r = (c^2/4 + (f*f)) /2f
• r = (c^2/4)/(2f) + f/2f
• r = c^2/(8f) + f/2
Conclusion (rayon):
Le calcul du rayon (r) d'un arc à partir de sa corde (c) et de sa flèche (f) peut être formulé de la façon suivante:

Exemple (suite):
Quel est le rayon d'un arc AB sachant que sa corde est égale à 11 cm et que sa flèche DE est égale à 2 cm (voir image ci-dessus)?
Il faut appliquer la formule:
• r = AB^2/(8*DE) + DE/2
• r = 11^2/(8*2) + 2/2
• r = 121/16 + 1
• r = 7,56 + 1
• r = 8,56 cm
Connaissant l'angle (a = 80°) et la rayon (r = 8,56 cm), il suffit d'appliquer la formule pour connaître la longueur de l'arc AB:
• r = 121/16 + 1
• r = 7,56 + 1
• r = 8,56 cm
• arc AB = (Pi*r*a) / 180
• arc AB = (Pi*8,56*80) / 180
• arc AB = 11,95 cm
• arc AB = 11,95 cm
Résultat final: un arc de 11 cm de corde et 2 cm de flèche a une longueur de 11,95 cm.
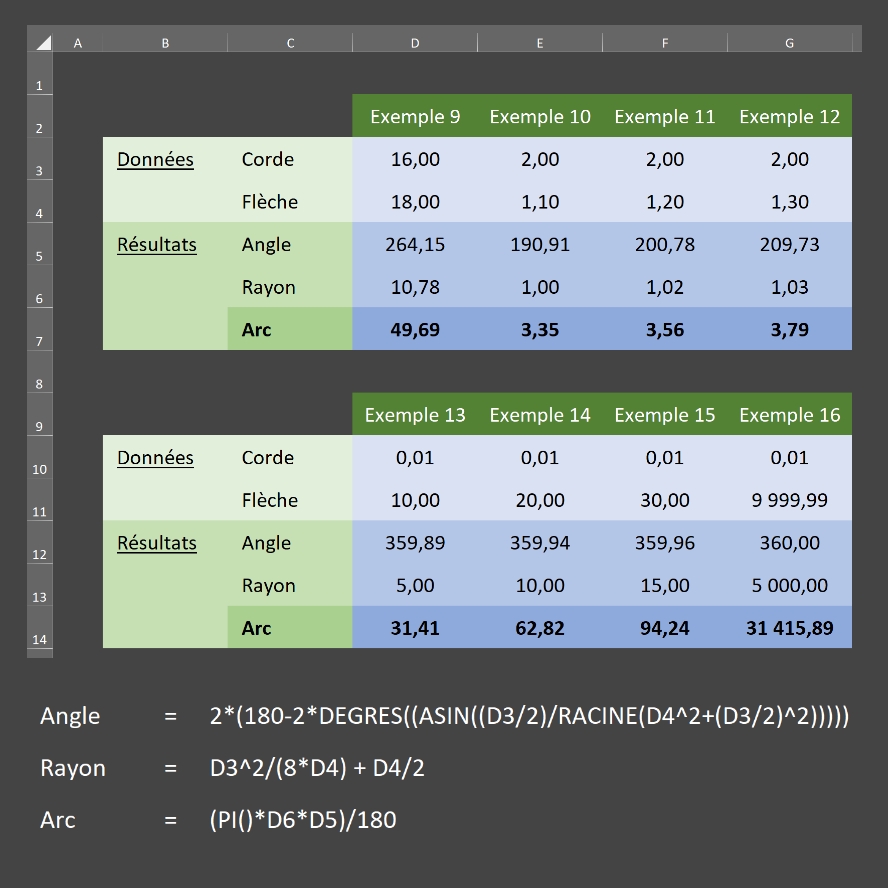
Autres exemples (ci-dessous):
(avec le tableur Excel de Microsoft)
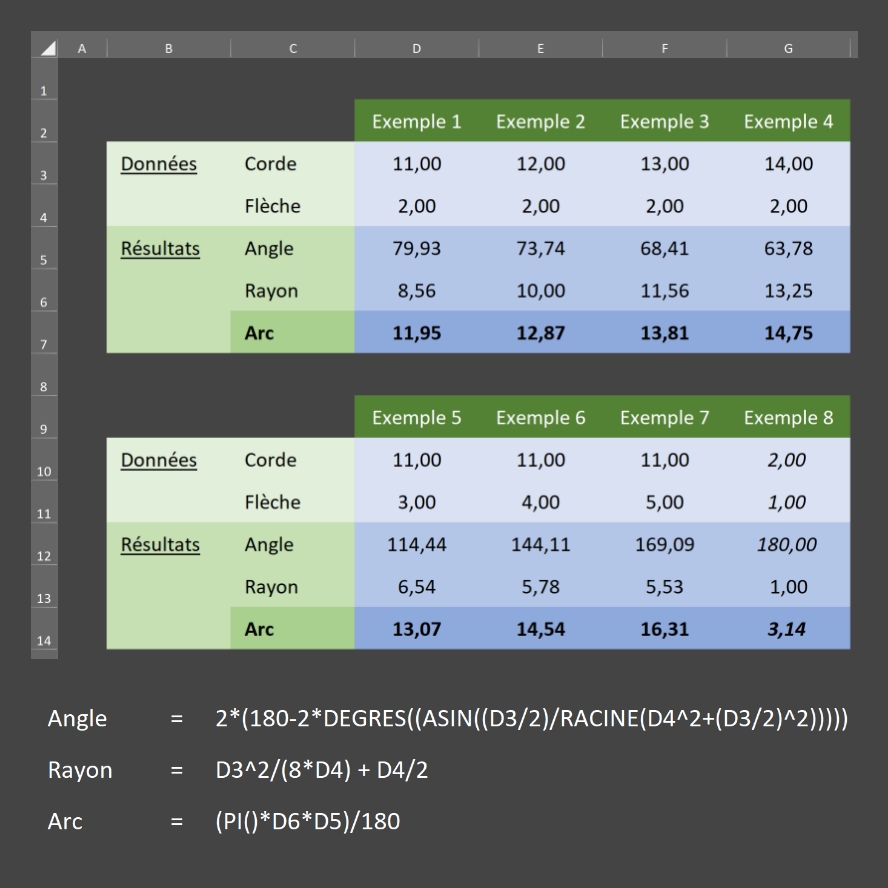
Notes (image ci-dessus):
- dans les formules qui appa-raissent, celle du calcul de l'angle contient une conversion de radians en degrés car les radians sont utlilisés par défaut dans le tableur Excel;
- l'exemple 8 est un cas particu-lier: une corde qui est égale au double de la flèche est le diamètre du cercle de l'arc et si la flèche vaut 1, alors l'arc vaut Pi (3,14);
- des toutes petites différences de calcul peuvent apparaître dues aux méthodes appliquées pour les arrondis.
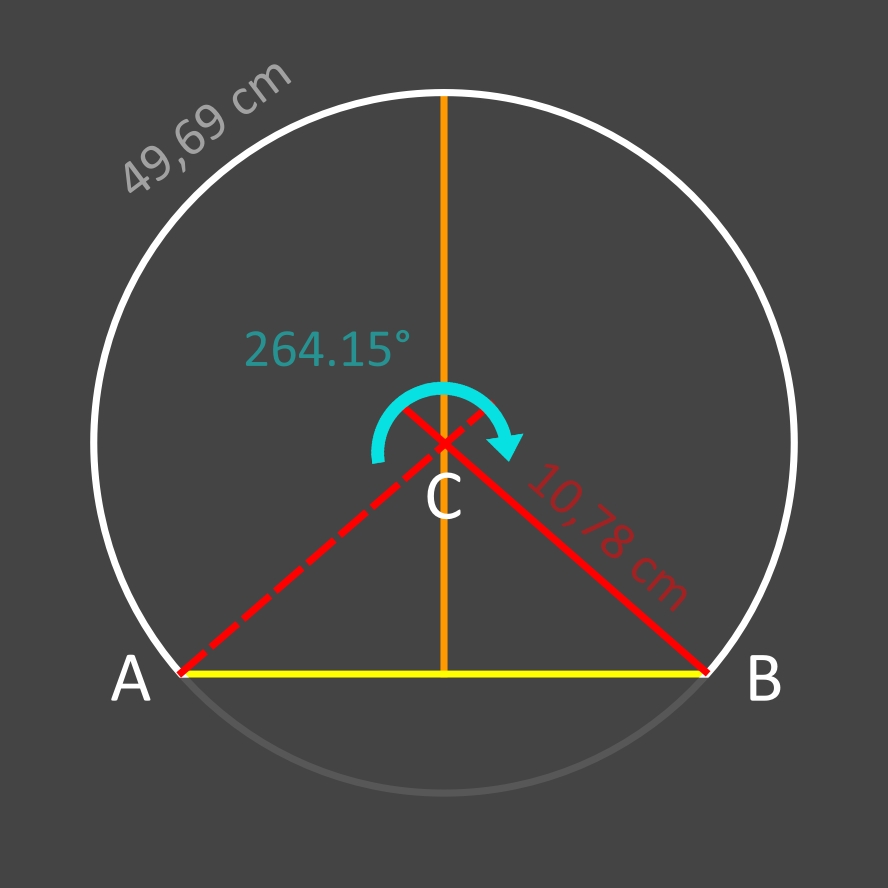
Arcs avec des angles > 180°:
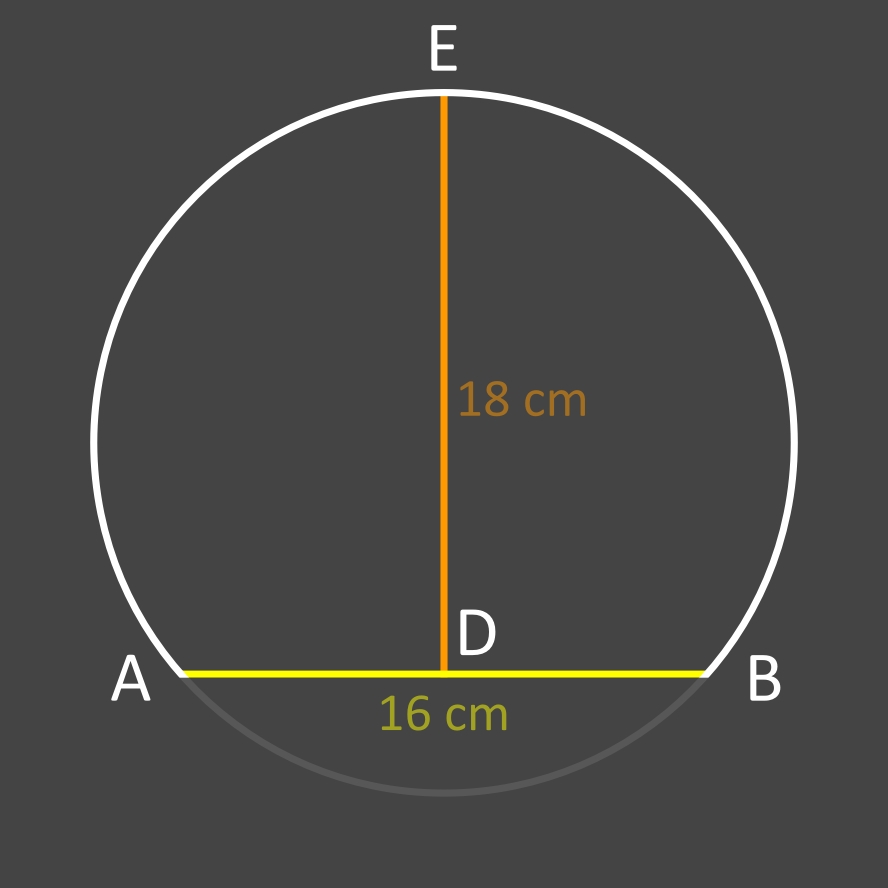
L'angle d'un arc est supérieur à 180° quand sa flèche est plus grande que le rayon du cercle (voir image ci-dessus).
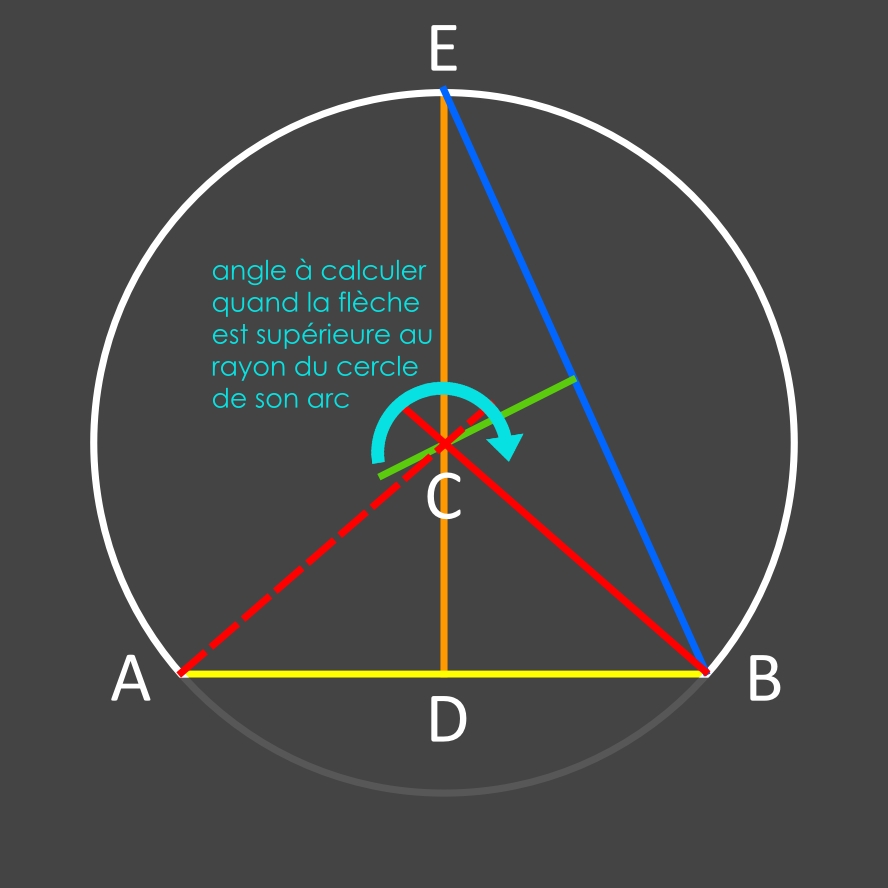
Avec une corde AB de 16 cm et une flèche DE de 18 cm, et en appliquant les mêmes formules développées plus haut, on obtiendra:
• l'angle (obtu) ACB = 264,15°
• le rayon CB = 10,78 cm
• l'arc AB = 49,69 cm
Report de ces trois résultats dans l'image ci-dessous:
Autres exemples (ci-dessous):
(toujours avec le tableur Excel)
• • •
• •
•
• •
•
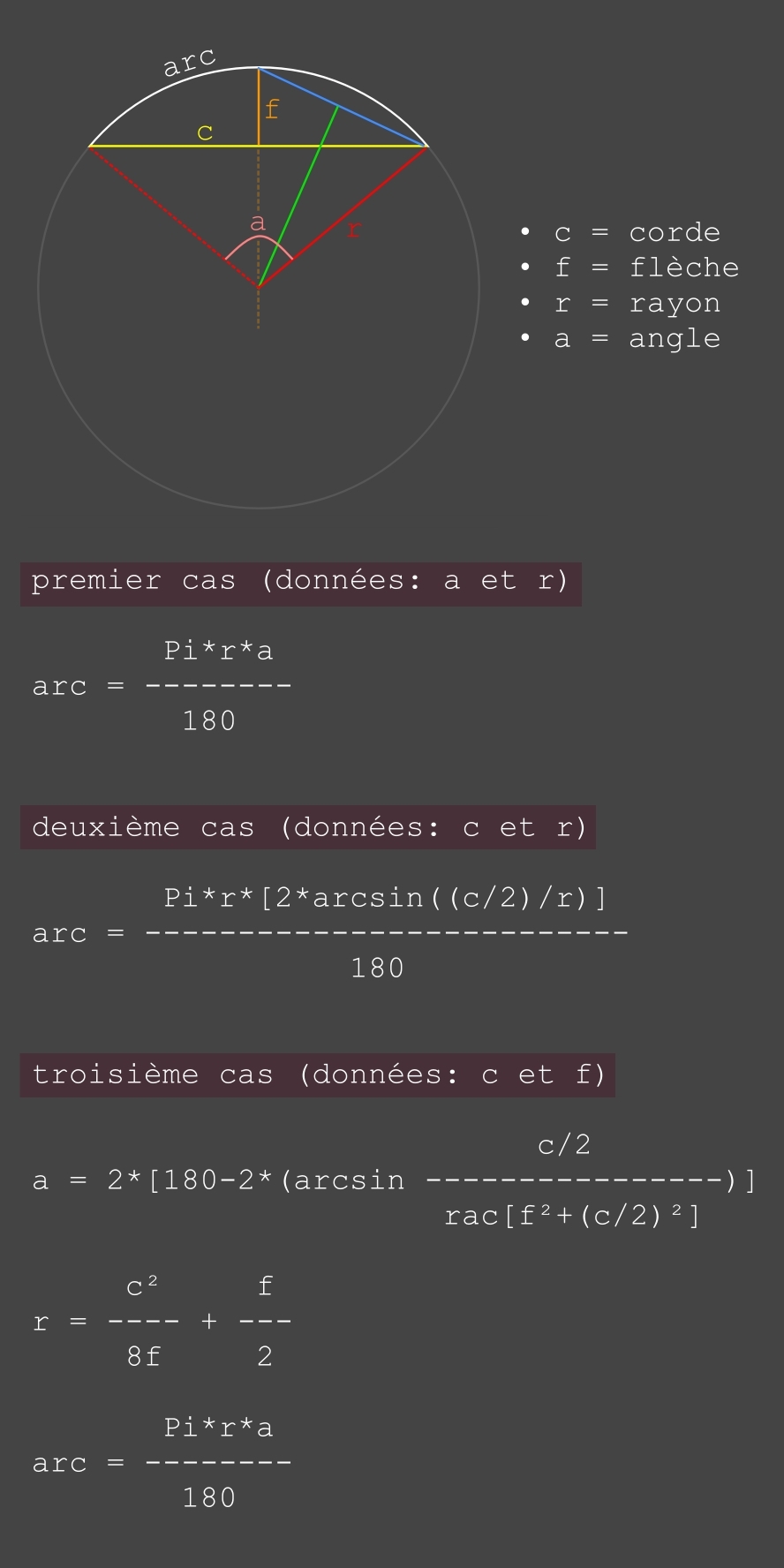
synthèse
• • •
• •
•
• •
•

