pour
comprendre
les paraboles
en commençant par
la forme canonique
comprendre
les paraboles
en commençant par
la forme canonique

"poisson" = 8 fonctions de paraboles + 1 fonction du cercle
(images que j'ai réalisées avec le logiciel DESMOS)
(images que j'ai réalisées avec le logiciel DESMOS)
Le mot canonique vient de canon, sans rapport ici avec une pièce d'artillerie. Canon signifie loi, règlement, précepte. Toute fonction du second degré possède une forme originelle dite forme canonique, où la variable x n'apparaît qu'une seule fois. La forme canonique permet de bien comprendre le comportement graphique des fonctions du second degré (les paraboles).
Le but de cette page est de proposer une bonne compréhension des paraboles en commençant par leur forme canonique, forme à partir de laquelle découle mathématiquement la forme développée (forme utilisée couramment).
Nous pouvons observer des paraboles dans de nombreuses circonstances: trajectoires de projectiles, câbles de ponts suspendus, chemins d'objets célestes, etc.
Les calculs paraboliques sont très utilisés dans la conception d'applications techniques et d'objets de la vie courante.
Note: dans cette page, tous les nombres sont considérés appartenant aux nombres réels (R), et sont donc exclus les nombres complexes (C).
Note: dans cette page, ne sont pas abordées les notions de Foyer et Directrice des paraboles qui feront l'objet d'une autre page, celle-ci étant volontairement focalisée sur seule la forme canonique.
plan de la page
(accès direct en cliquant sur les yeux)
a) parabole (définition)....(•_•)
b) parabole f(x) = x².......(•_•)
c) translation en x.........(•_•)
d) translation en y.........(•_•)
e) coefficient (a)..........(•_•)
f) forme canonique..........(•_•)
g) forme développée.........(•_•)
h) conclusion (application).(•_•)
i) parabole de StarShipTwo..(•_•)
b) parabole f(x) = x².......(•_•)
c) translation en x.........(•_•)
d) translation en y.........(•_•)
e) coefficient (a)..........(•_•)
f) forme canonique..........(•_•)
g) forme développée.........(•_•)
h) conclusion (application).(•_•)
i) parabole de StarShipTwo..(•_•)
a) parabole (définition)
01
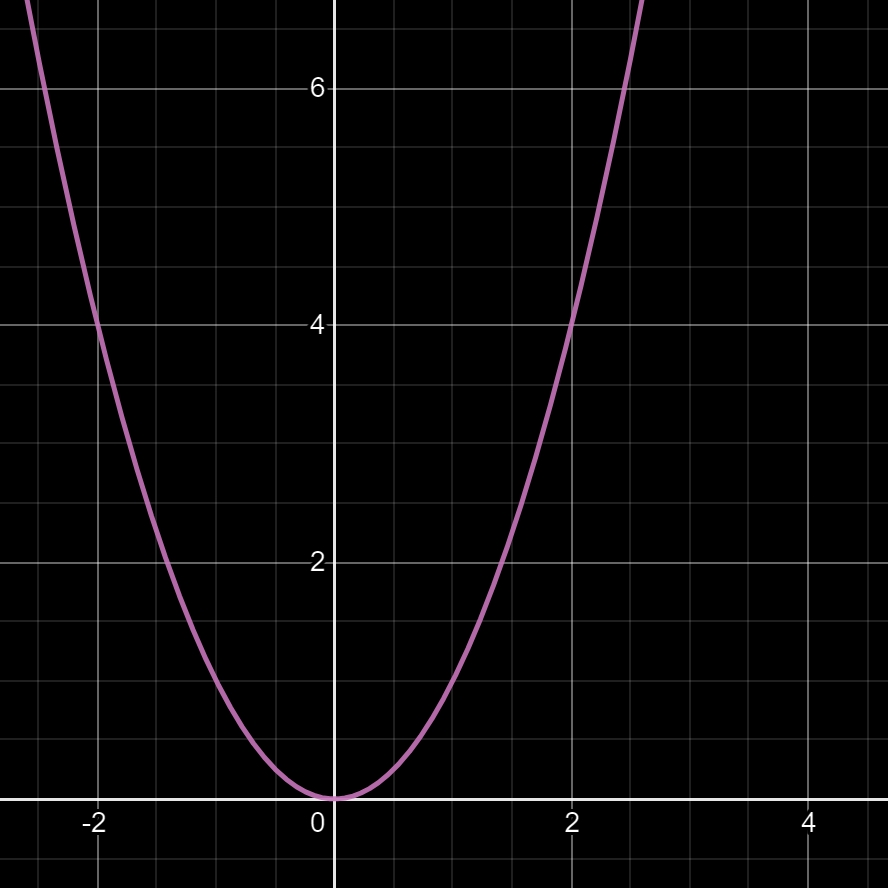
Une parabole est la courbe plane représentative d'une fonction du second degré.
La parabole la plus simple est définie par la fonction f(x) = x².
b) f(x) = x²
02
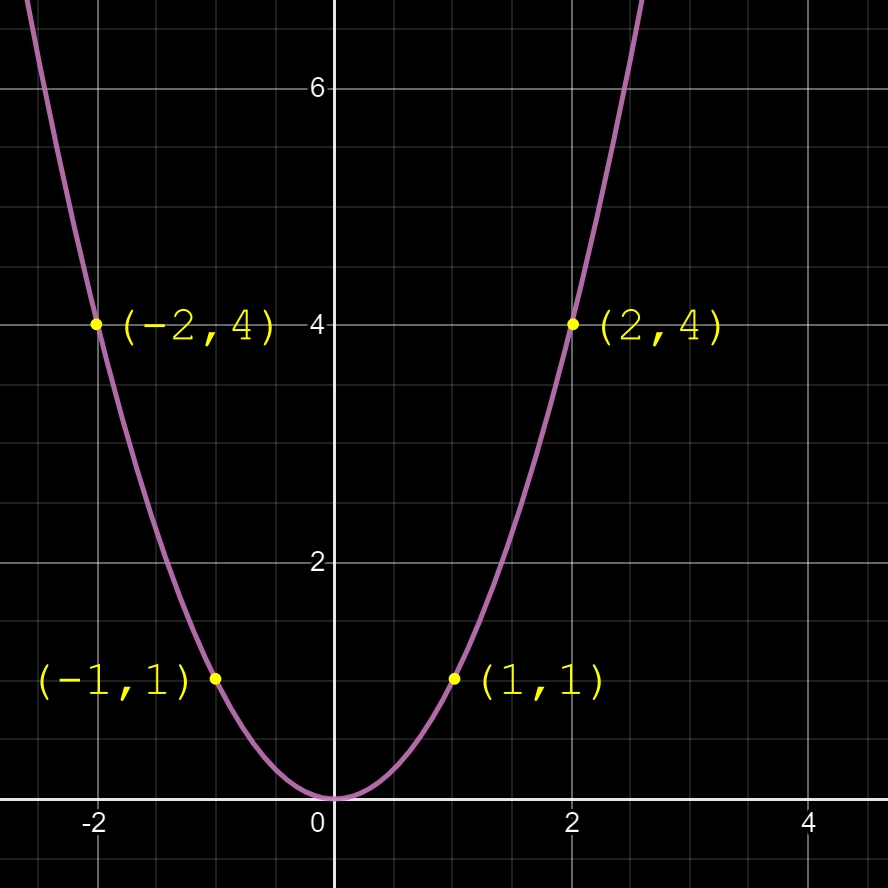
Sachant que (+x)² = (-x)², on peut dire que dans la fonction f(x) = x² tout point de +x et de son opposé -x donnent la même valeur y.
Une parabole est, en conséquence, une courbe symétrique. Son axe de symétrie étant une droite passant par sa base (ou par son sommet) et parallèle à l'axe des y (axe des ordonnées).
Dans la fonction f(x) = x², l'axe de symétrie de la parabole est l'axe des y et la base de la parabole est le point (0,0).
c) translation en x
03
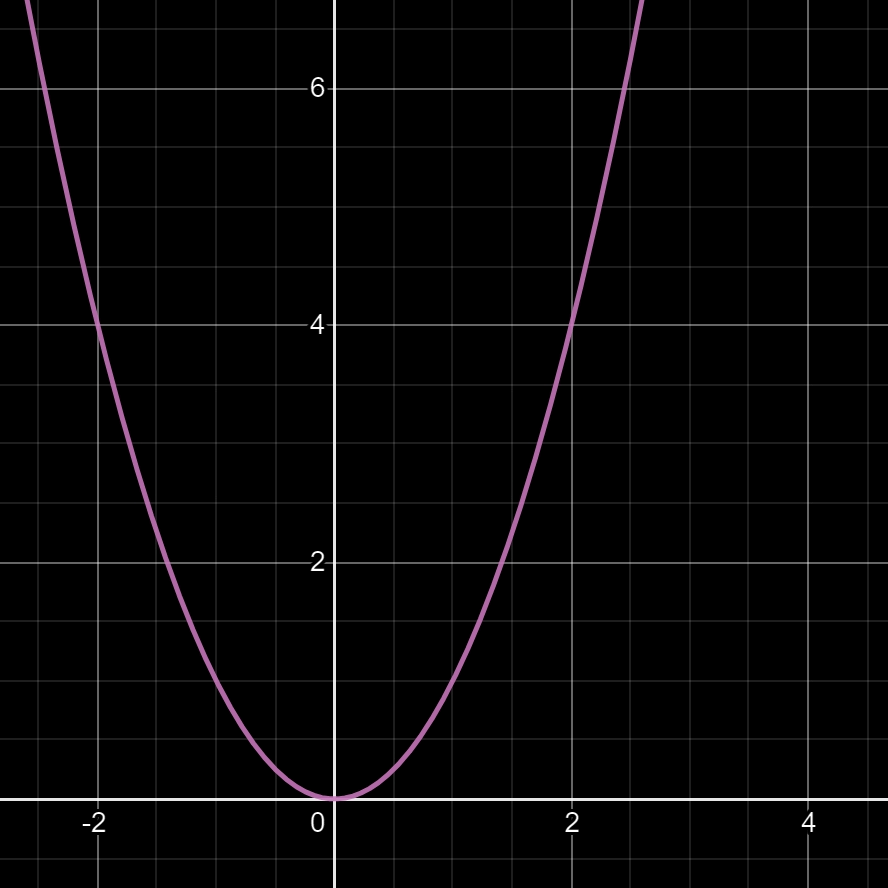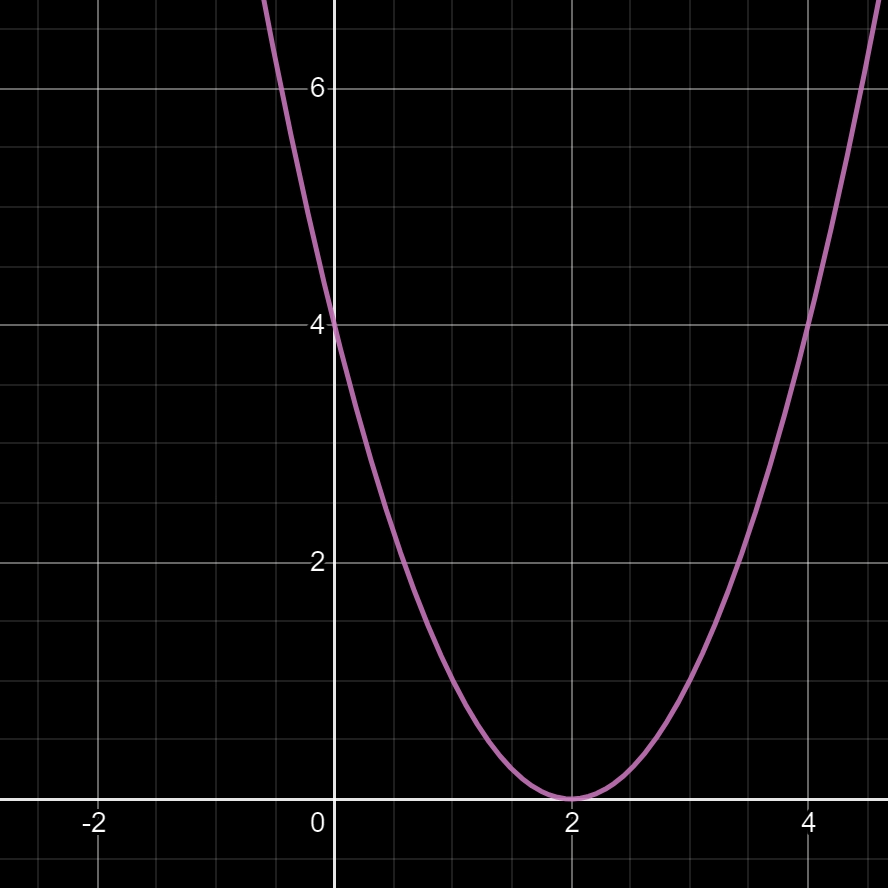
Question: que faut-il faire pour décaler la parabole de la fonction f(x) = x² de 2 unités vers la droite, comme si on procédait à un glissement latéral sur l'axe des x (abscisses) ?
Réponse dans l'image ci-dessous.
Note: en mathématique, on ne parle pas de décalage ou de glissement mais de translation.
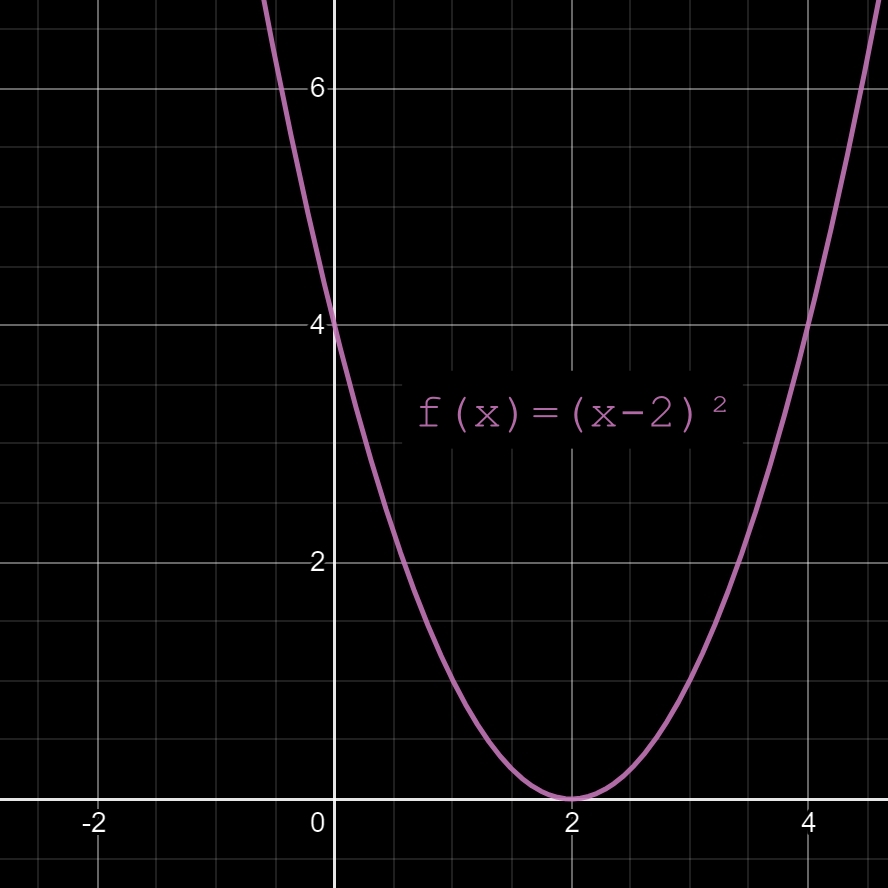
04
Pour une translation de α (alpha) unités le monôme x² devient alors le binôme (x - α)² avec:
• α > 0 → translation vers la droite
• α < 0 → translation vers la gauche
En conséquence, pour translater de 2 unités vers la droite la fonction f(x) = x² devient:
• f(x) = (x - (+2))²
• f(x) = (x - 2)²
Si on avait eu à translater de 4 unités vers la gauche, la fonction f(x) = x² aurait été:
• f(x) = (x - (-4))²
• f(x) = (x + 4)²
d) translation en y
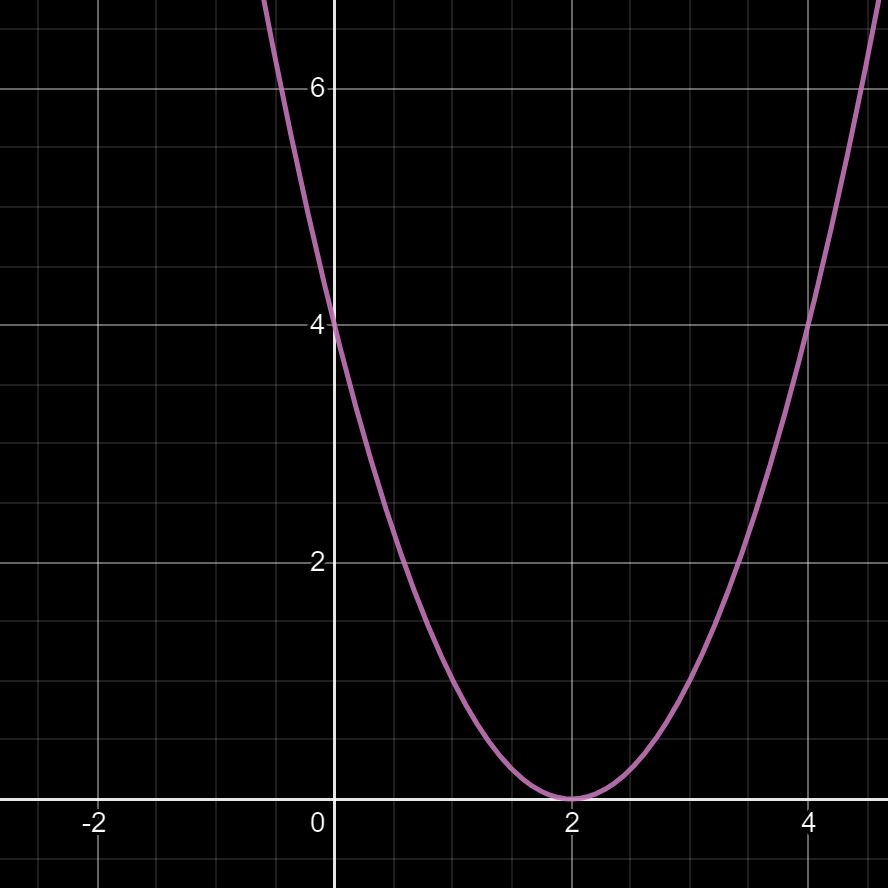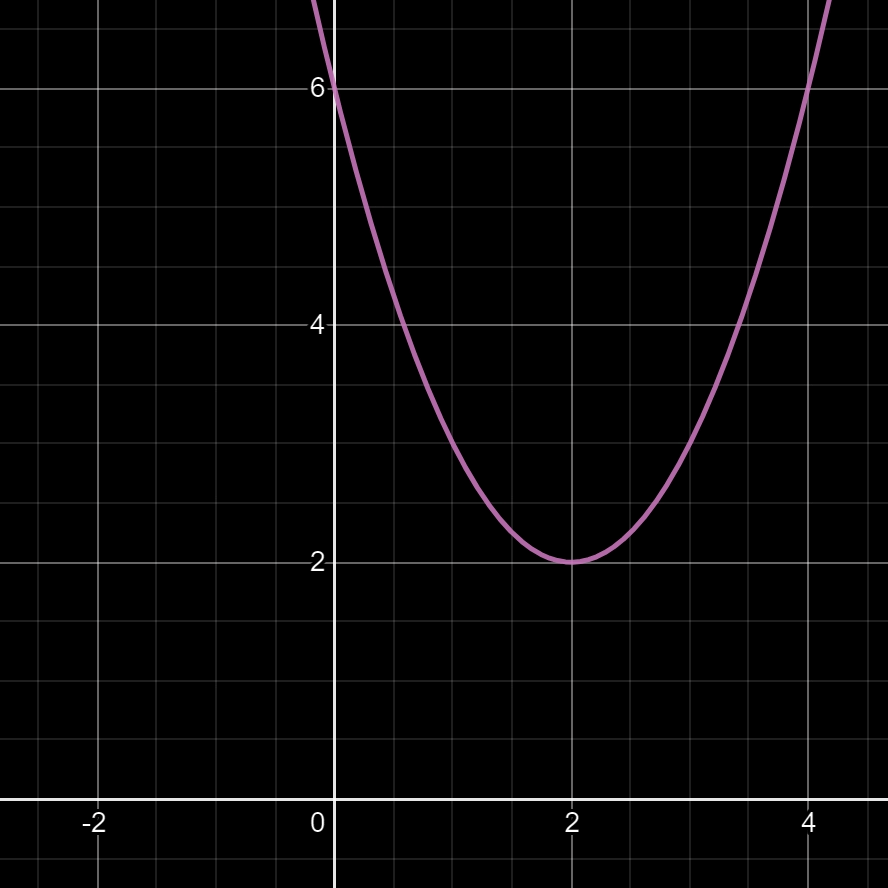
05
Question: que faut-il faire pour translater la parabole de la fonction f(x) = (x - 2)² de 2 unités vers le haut ?
Réponse dans l'image ci-dessous.
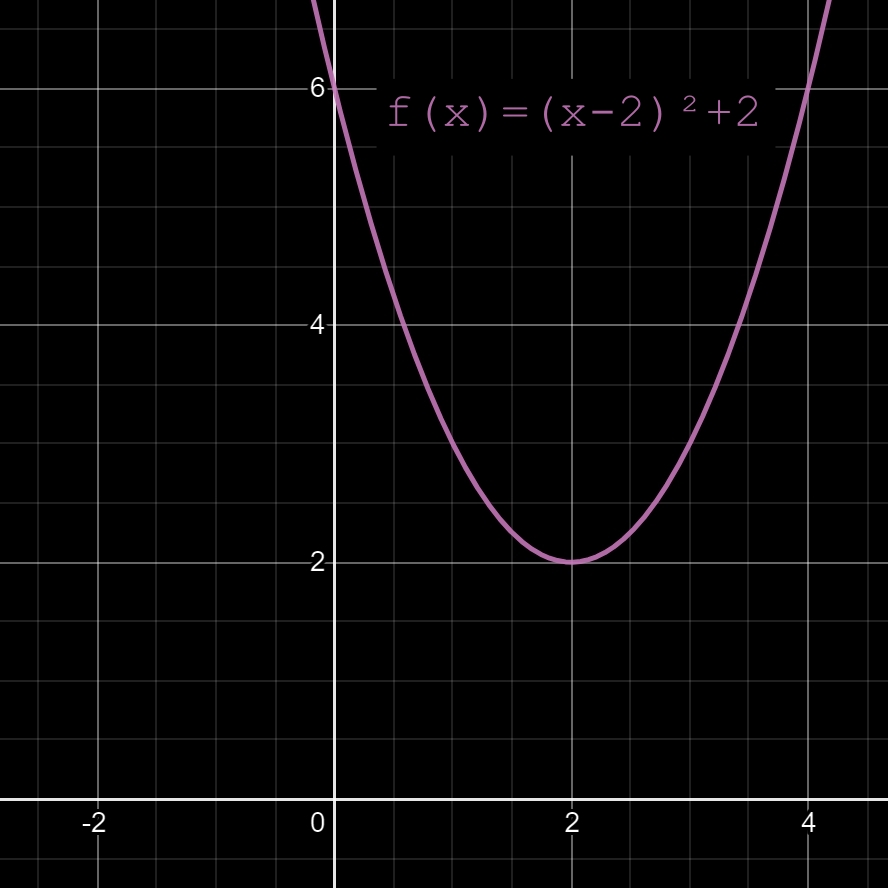
06
Pour une translation de β (bêta) unités le binôme (x - α)² devient alors le trinôme (x - α)² + β avec:
• β > 0 → translation vers le haut
• β < 0 → translation vers le bas
En conséquence, pour translater de 2 unités vers le haut, on obtiendrait:
• f(x) = (x - 2)² + 2
Si on avait eu à translater de 3 unités vers le bas, on aurait obtenu:
• f(x) = (x - 2)² - 3
e) coefficient (a)
07
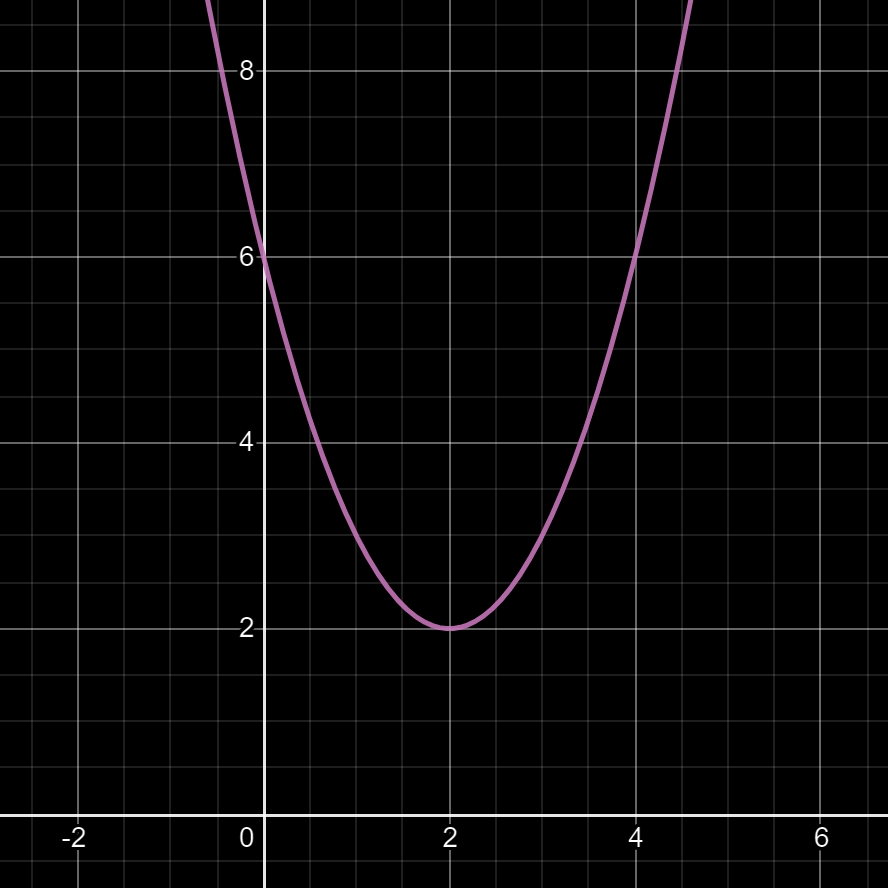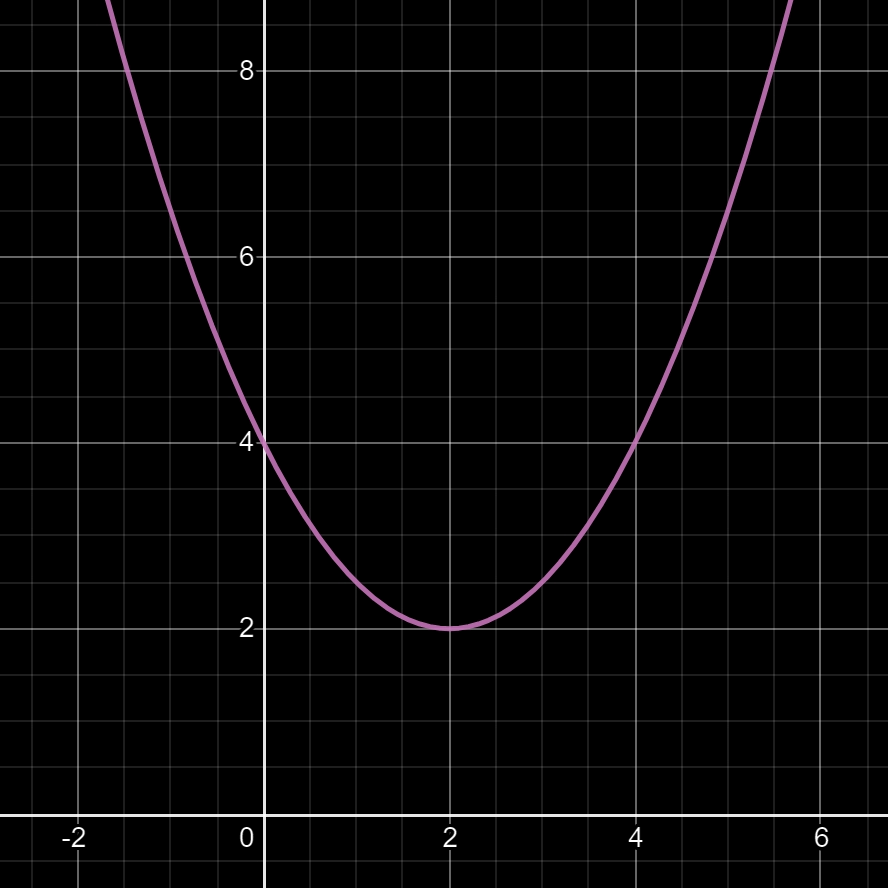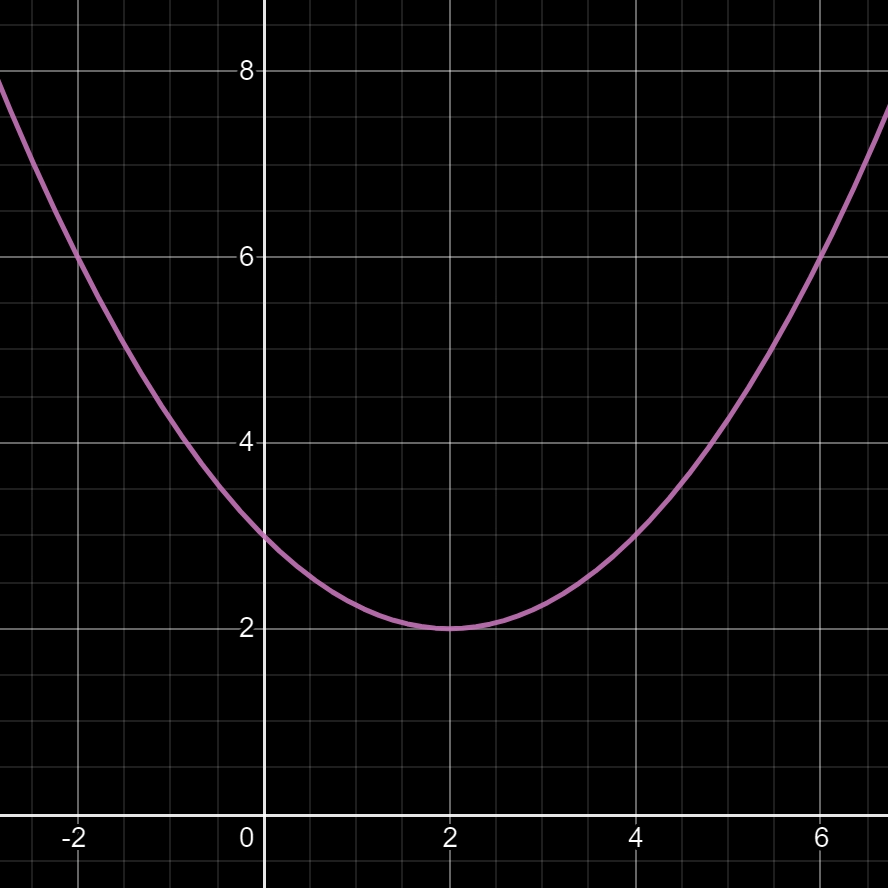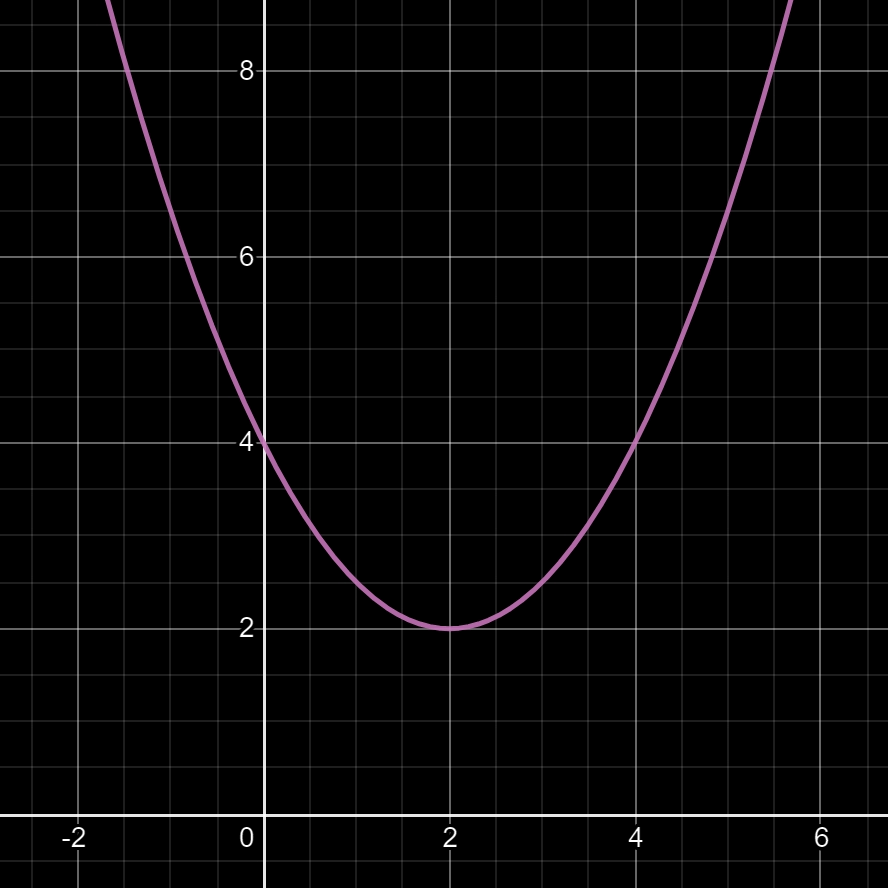
Question: que faut-il faire pour écarter ou reserrer les deux branches de la parabole de la fonction f(x) = (x - 2)² + 2 ?
Réponse dans l'image ci-dessous.
08
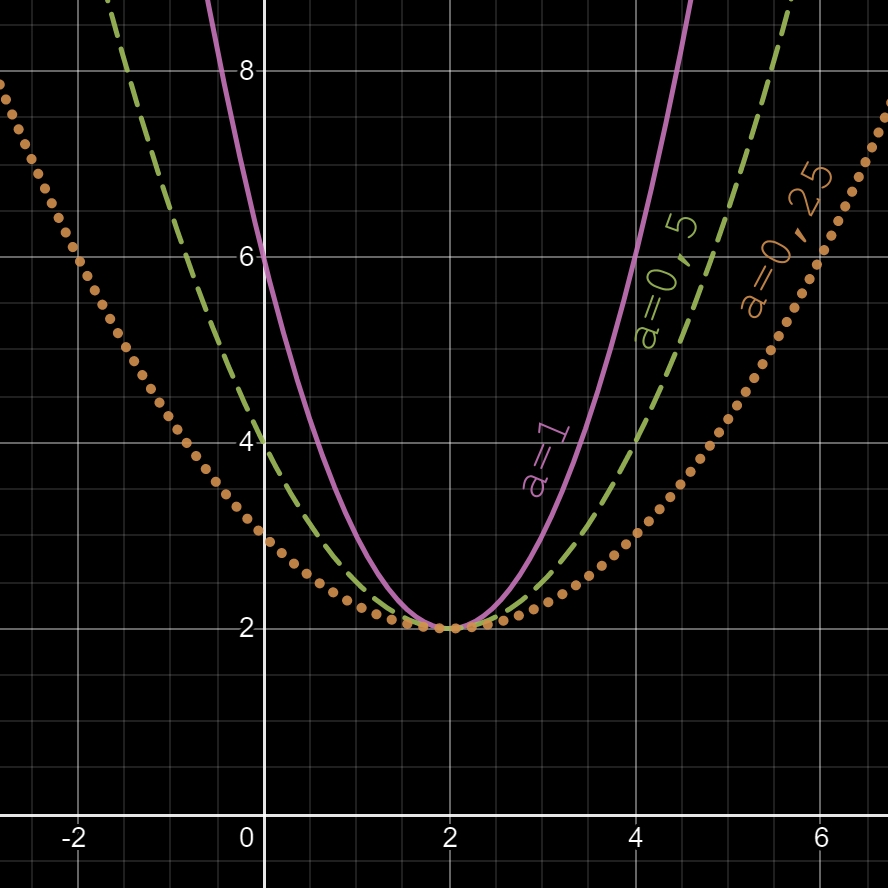
Pour écarter ou reserrer les branches d'une parabole, il faut appliquer un coefficient (appelé a) au premier monôme (celui qui est au carré) de la fonction f(x), et on obtiendra:
f(x) = a(x - α)² + β
Note:
• si a > 0 → parabole = convexe (∪)
• si a < 0 → parabole = concave (∩)
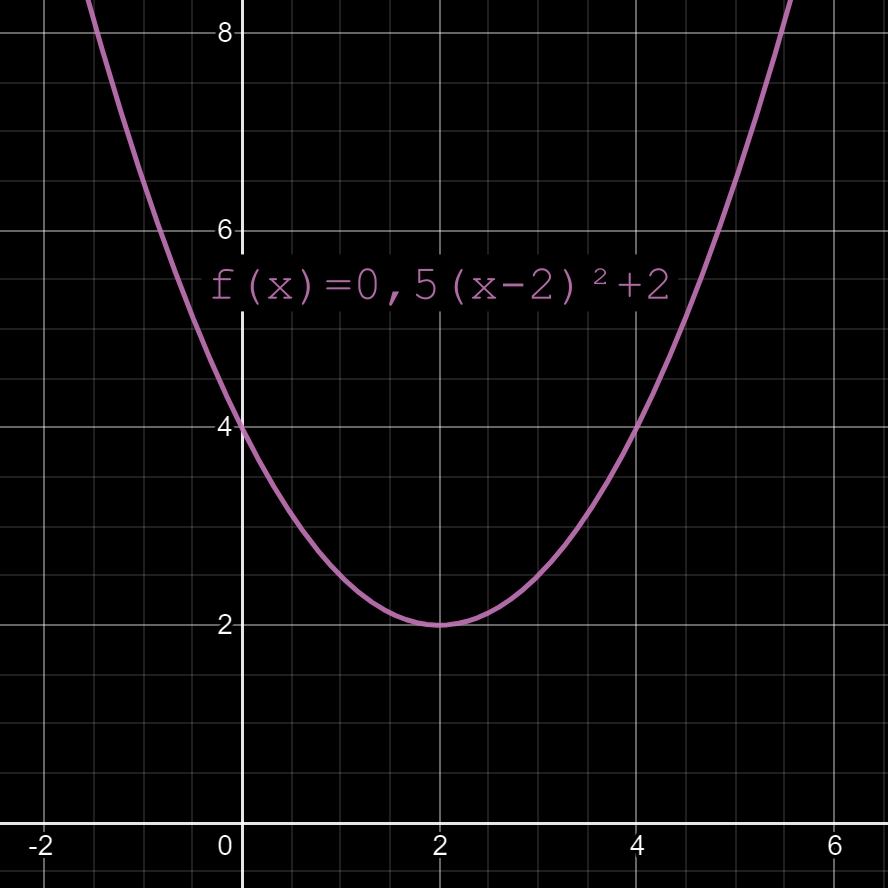
09
Exemple (ci-dessus) de la fonction f(x) = 0,5(x - 2)² + 2
f) forme canonique
La forme canonique d'une fonction est porteuse de sens puisqu'elle donne de l'information sur l'allure de son graphique. La forme canonique permet de reconnaître la repré-sentation graphique, instantanément.
La forme canonique d'une parabole se présente, in fine, de la façon suivante:

f(x) = a(x - α)² + β
Rappel:
• a → le coefficient d'ouverture
• α → la valeur de translation en x
• β → la valeur de translation en y
g) forme développée
En développant une fonction présentée sous la forme canonique, nous la transformons en une somme d’éléments. Ainsi nous allons générer la même fonction mais présentée sous une forme dite développée.
Développons donc l'exemple canonique des précédentes sections:
• f(x) = 0,5(x - 2)² + 2
• f(x) = 0,5(x² - 2*x*2 + 2²) + 2
• f(x) = 0,5(x² - 4x + 4) + 2
• f(x) = 0,5x² - 0,5*4x + 0,5*4 + 2
• f(x) = 0,5x² - 2x + 2 + 2
• f(x) = 0,5x² - 2x + 4
forme canonique
f(x) = 0,5(x - 2)² + 2
↓ ↓ ↓
forme développée
f(x) = 0,5x² - 2x + 4
f(x) = 0,5(x - 2)² + 2
↓ ↓ ↓
forme développée
f(x) = 0,5x² - 2x + 4
Prenons un autre exemple:
• f(x) = -3(x + 2)² - 6
• f(x) = -3(x² + 2*x*2 + 2²) - 6
• f(x) = -3(x² + 4x + 4) - 6
• f(x) = -3x² + (-3)*4x + (-3)*4 - 6
• f(x) = -3x² - 12x - 12 - 6
• f(x) = -3x² - 12x - 18
forme canonique
f(x) = -3(x + 2)² - 6
↓ ↓ ↓
forme développée
f(x) = -3x² - 12x - 18
f(x) = -3(x + 2)² - 6
↓ ↓ ↓
forme développée
f(x) = -3x² - 12x - 18
La forme développée est la forme générale des fonctions du second degré (paraboles) du type:

f(x) = ax² + bx + c
forme canonique
f(x) = a(x - α)² + β
↓ ↓ ↓
forme développée
f(x) = ax² + bx + c
f(x) = a(x - α)² + β
↓ ↓ ↓
forme développée
f(x) = ax² + bx + c
h) conclusion (application)
La forme canonique permet une excellente approche pédagogique facilitant la compréhension et l'usage de la forme développée (dite forme générale).
La forme canonique est également un outil très utile. En voici un exemple:

10
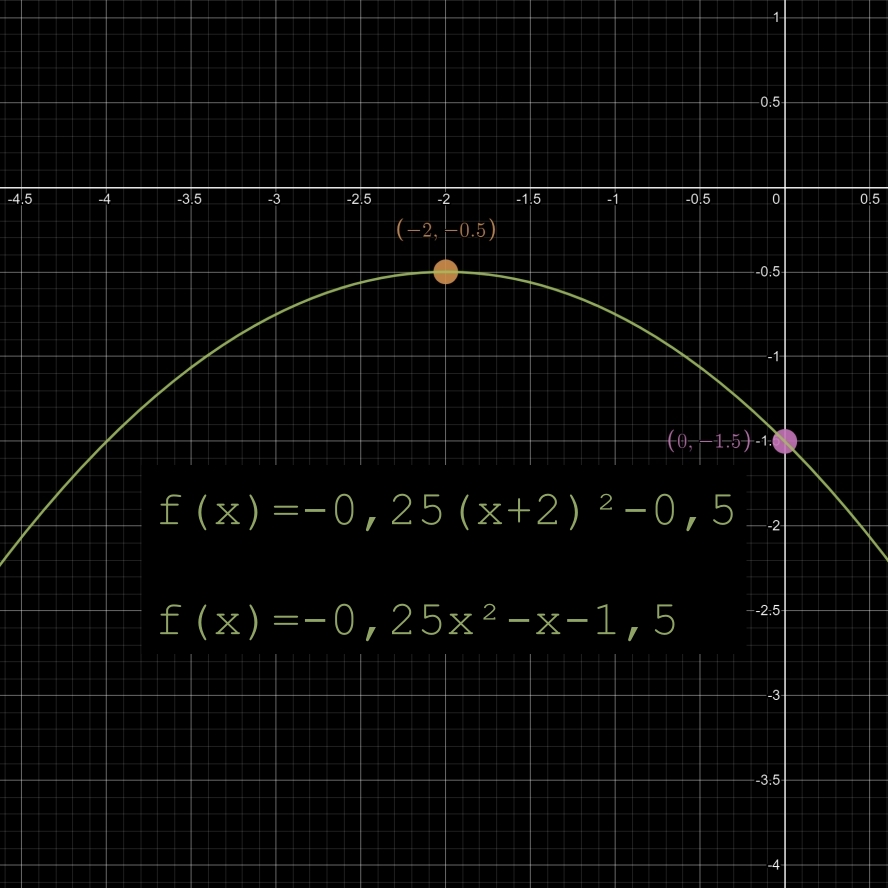
Soit deux points (image ci-dessus) aux coordonnées suivantes:
• point orange: x = -2; y = -0,5
• point rose: x = 0; y = -1,5
Question: sachant que le point orange est le sommet d'une parabole, quelle est la fonction, sous formes canonique et développée, de la parabole qui passe par ces deux points ?
Réponse:
1) forme canonique:
• f(x) = a(x - α)² + β
• α = x (du point orange) = -2
• β = y (du point orange) = -0,5
• f(x) = a(x - (-2))² + (-0,5)
• f(x) = a(x + 2)² - 0,5
• y = a(x + 2)² - 0,5
• calcul de a (on connaît x et y)
• x = 0 (du point rose)
• y = -1,5 (du point rose)
• -1,5 = a(0 + 2)² - 0,5
• -1,5 = 4a - 0,5
• 4a = -1,5 + 0,5
• 4a = -1
• a = -1/4 = -0,25
• f(x) = -0,25(x + 2)² - 0,5
2) forme développée:
• f(x) = -0,25(x + 2)² - 0,5
(x + 2)² = x² + 2*x*2 + 2²
(x + 2)² = x² + 4x + 4
(x + 2)² = x² + 4x + 4
• f(x) = -0,25(x² + 4x + 4) - 0,5
• f(x) = -0,25x² - x - 1 - 0,5
• f(x) = -0,25x² - x - 1,5
11
i) parabole de StarShipTwo
Autre (et dernier) exemple ...
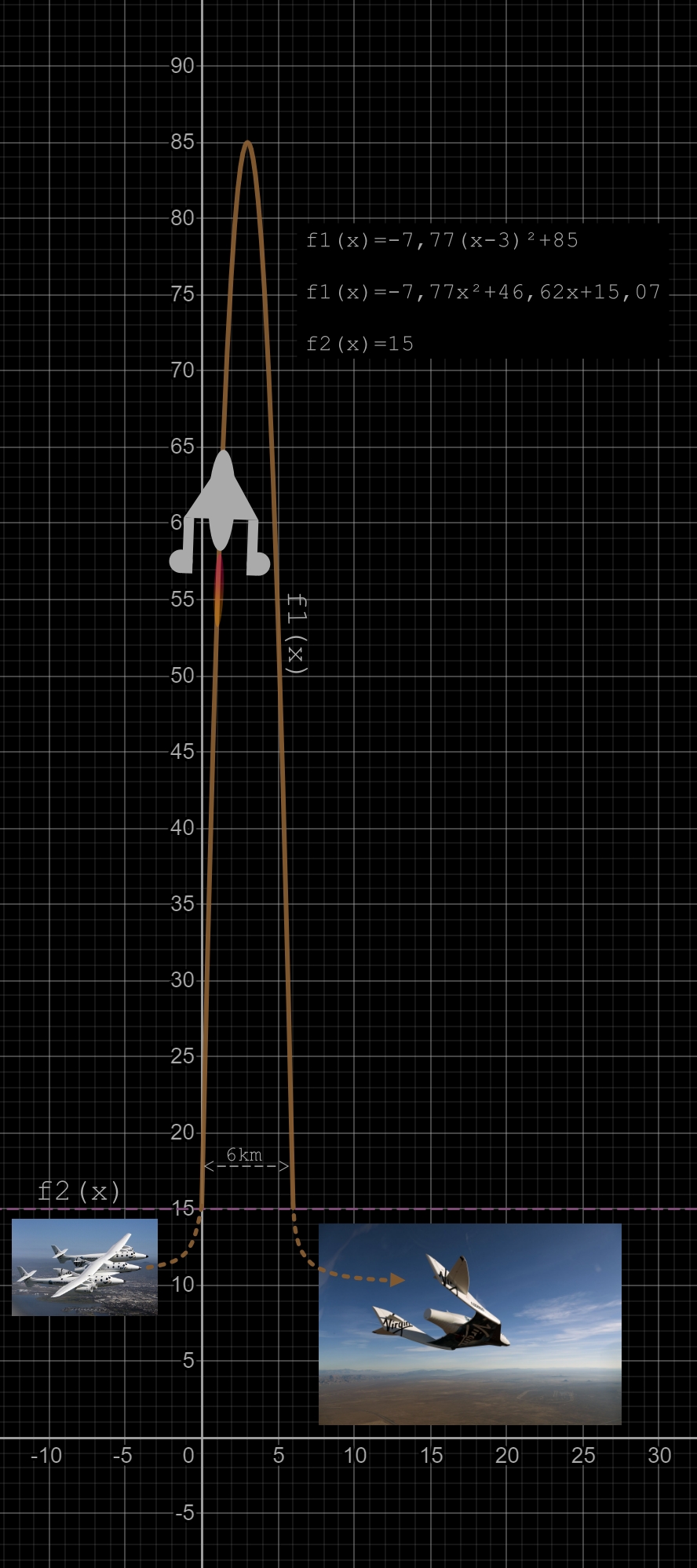
StarShipTwo est un avion spatial qui a décollé à une altitude de 15 km (50000 pieds) depuis un avion porteur (WhiteKnightTwo) le dimanche 11 juillet 2021.
StarShipTwo, telle une fusée, est montée à l'altitude de 85 km, donc tout près du niveau à partir de laquelle l'atmosphère terrestre devient trop ténue pour des applications aéronautiques. C'est la frontière entre l' atmosphère terrestre et l'espace.
L'avion spatial StarShipTwo comprend 2 pilotes et 6 passagers maximum. Fabriqué par Virgin Galactic, cet avion spatial effectuait un vol avec Richard BRANSON, fondateur de la société Virgin et avec quelques autres passagers.
Pour tracer la parabole de ce vol, il faut les coordonnées de 2 points comme expliqué dans la précédente section. Il faut les coordonnées du sommet de la parabole et celle de n'importe quel point de cette parabole.
Considérons le point (x=0 et y=15) correspondant au point de décollage de l'avion spatial. Quant au sommet de la parabole, il passera par y=85 pour x=3 (3 étant la moitié des 6 km qui sont l'écart de la base de la parabole).
Note: les 6 km sont une donnée fondamentale trouvée dans les rapports communiqués par la presse.
Note: StarShipTwo est un véhicule autonome (qui possède ses propres moyens de propulsion et de vol). En conséquence, parler d'un vol purement parabolique serait une erreur. Il s'agit seulement d'un exercice pour définir la fonction de la parabole qui s'approcherait de la forme du vol accompli par l'avion spatial.
Note: StarShipTwo est un véhicule autonome (qui possède ses propres moyens de propulsion et de vol). En conséquence, parler d'un vol purement parabolique serait une erreur. Il s'agit seulement d'un exercice pour définir la fonction de la parabole qui s'approcherait de la forme du vol accompli par l'avion spatial.
Calcul de la f(x) de la parabole ...
1) forme canonique:
• f(x) = a(x - α)² + β
• α = 3 (sommet en x)
• β = 85 (sommet en y)
• f(x) = a(x - (+3))² + 85
• f(x) = a(x - 3)² + 85
• y = a(x - 3)² + 85
• calcul de a (on connaît x et y)
• x = 0 (autre point en x)
• y = 15 (autre point en y)
• 15 = a(0 - 3)² + 85
• 15 = a(-3)² + 85
• 15 = a9 + 85
• -a9 = 85 - 15
• -a9 = 70
• a = 70/-9 = -7,77
• f(x) = -7,77(x - 3)² + 85
2) forme développée:
• f(x) = -7,77(x - 3)² + 85
(x - 3)² = x² - 2*x*3 + 3²
(x - 3)² = x² - 6x + 9
(x - 3)² = x² - 6x + 9
• f(x) = -7,77(x² - 6x + 9) + 85
• f(x) = -7,77x² + 46,62x - 69,93 + 85
• f(x) = -7,77x² + 46,62x - 69,93 + 85
• f(x) = -7,77x² + 46,62x + 15,07
12
Pour information: après avoir passé l'apogée de la parabole (à 85 km d'altitude) l'avion spatial est entré dans une séquence de micro-gravitée, puis les ailes se sont repliées (comme sur l'image ci-dessous) afin de maintenir l'avion dans une position stable pendant sa descente dans l'atmosphère. Cette fonctionnalité porte le nom de "feather mechanism". Le terme "à plumes" est utilisé car la configuration fait penser à un volant de badminton.

13
