calcul d'une
distance maximale
entre une poutre
et un poids
distance maximale
entre une poutre
et un poids

Guillaume François Antoine, marquis De L'HÔPITAL, né à Paris en 1661, fut un mathématicien français. Il est l'auteur du premier livre en français sur le calcul différentiel (*). Il est décédé en 1704 (il avait 43 ans).
(*) Note: le calcul intégral étudie l'aire sous une courbe, le calcul différentiel étudie les variations (dérivées) d'une courbe.

I. Question:
Guillaume de L'HÔPITAL avait proposé le problème suivant:
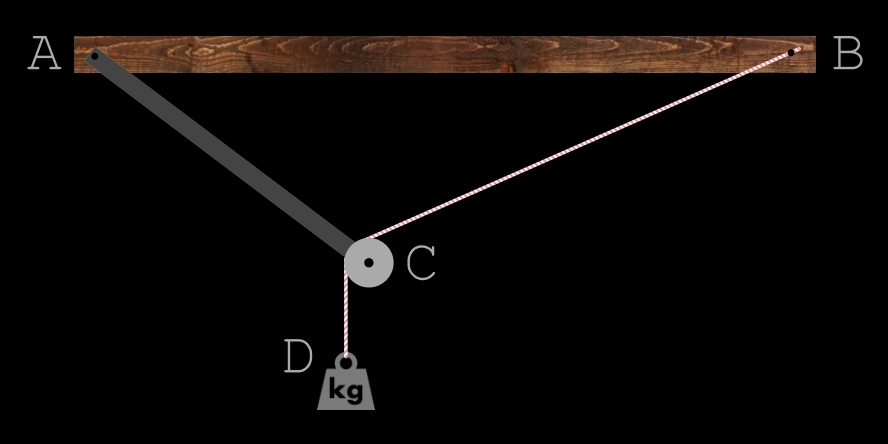
Sur une poutre horizontale de 100 cm de long est fixée une tige (libre) de 40 cm au bout de laquelle est montée un poulie.
De l'autre côté est fixée une corde de 100 cm qui passe sur la poulie et qui est ensuite lestée par un poids (sans importance sur sa valeur).
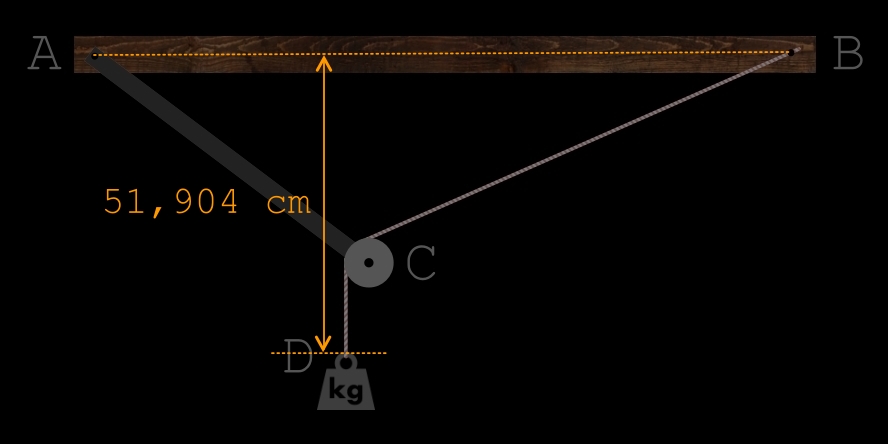
Il faut calculer la plus grande distance que l'on peut obtenir entre la poutre et le poids (le bout de la corde).
Récapitulatif:
• Poutre AB = 100 cm
• Corde BD = 100 cm (via C)
• Tige AC = 40 cm
Quelle est la distance verticale et maximum qu'il peut y avoir entre la poutre AB et le bout de la corde (en D) ?

II. (Ma) réponse:
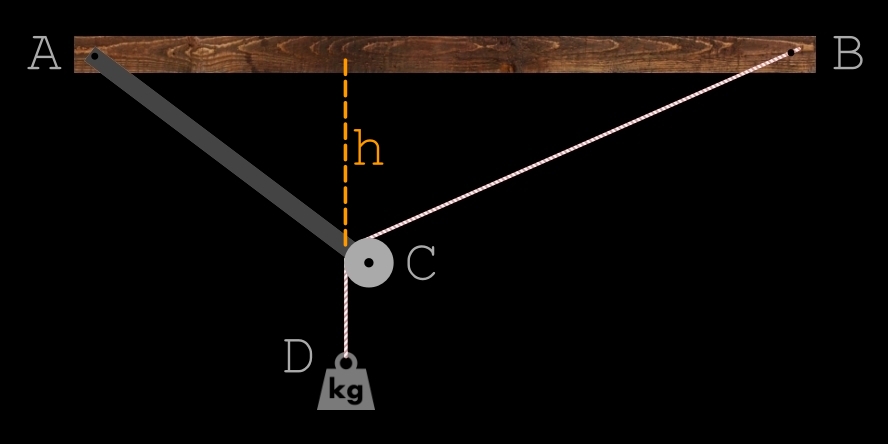
Soit le triangle ABC.
On sait que AB = 100 cm et AC = 40 cm.
Quant à BC, il peut aller de 61 à 100 cm (*).
(*) Note: En géométrie, l'inégalité triangulaire est le fait que, dans un triangle, la longueur d'un côté est inférieure à la somme des longueurs des deux autres côtés.
Ma solution passe par la géométrie.L'objectif étant de calculer, pour chaque longueur du côté BC (de 61 à 100 cm), la hauteur h du triangle ABC (en prenant AB comme base).
On peut calculer la hauteur d'un triangle à partir de son aire mais pour calculer l'aire d'un triangle il faut connaître la hauteur, sauf si on utilise la formule de Héron d'Alexandrie (*) qui permet de calculer l'aire d'un triangle seulement à partir de la longueur des 3 côtés.
(*) Rappel sur la formule:

Ci-dessous, les 4 premières étapes calculent l'aire du triangle ABC avec x (variant de 61 à 100 cm) représentant le côté BC (et avec p pour périmètre et a pour aire).
L'étape numéro 5 calcule la hauteur h (pour x variant de 61 à 100 cm).
Et enfin, la dernière étape (numéro 6) finalise la fonction qui va tracer la courbe représentative des hauteurs (axe des x) pour chaque longueur de BC (axe des y) entre 61 et 100 cm.
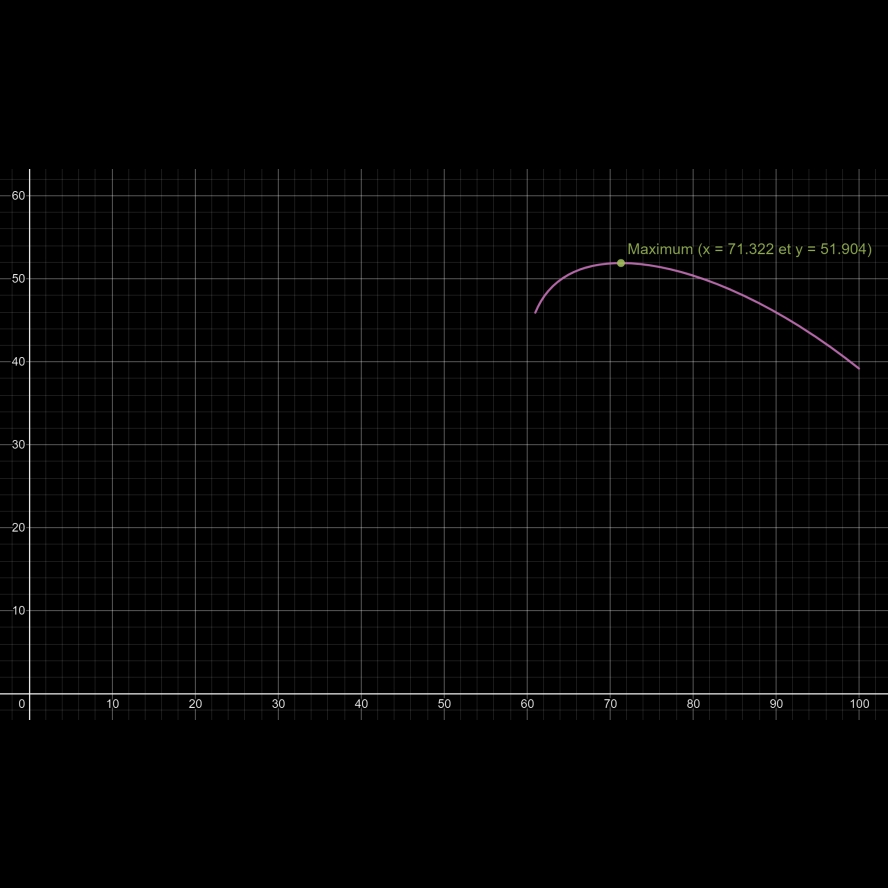
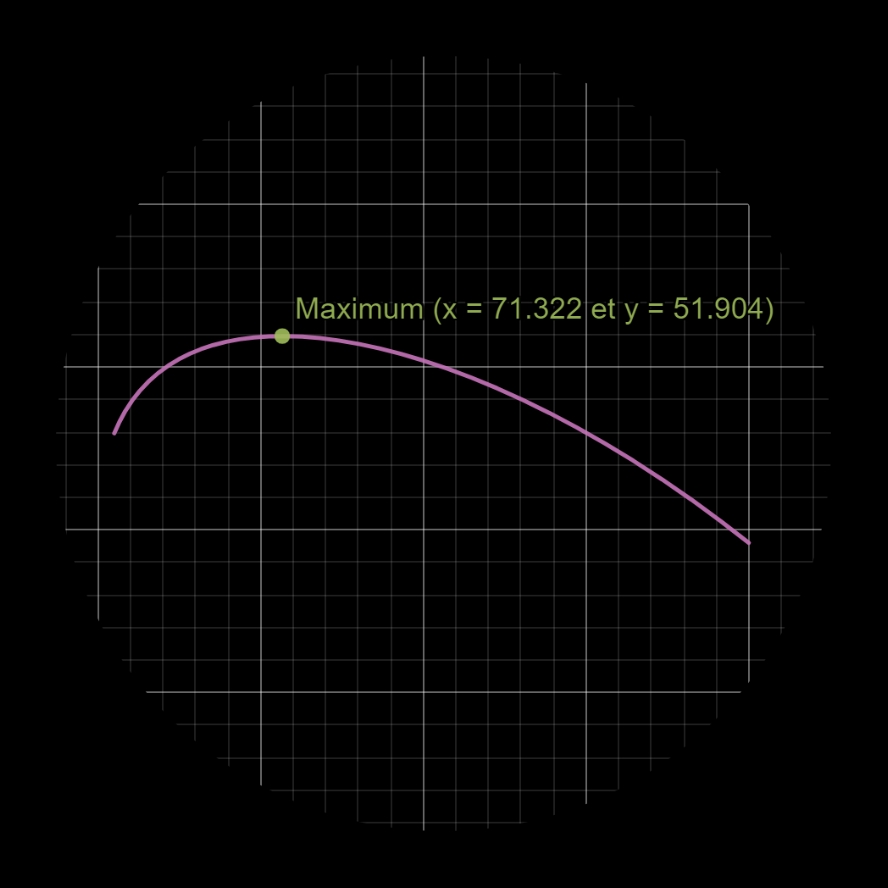
Le point maximum de la courbe donne alors la réponse au problème: 51,904 cm
Voici donc les 6 étapes du calcul de la fonction:
1) p = 100 + 40 + x {x ≥ 61}{x ≤ 100}
2) s = p/2
3) a² = s * (s - 100) * (s - 40) * (s - x)
4) a = racine(a²)
5) h = a / (0,5 * 100)
6) f(x) = h + (100 - h)
2) s = p/2
3) a² = s * (s - 100) * (s - 40) * (s - x)
4) a = racine(a²)
5) h = a / (0,5 * 100)
6) f(x) = h + (100 - h)
Note: les 3 images ci-dessous ont été générées avec l'éditeur de graphes DESMOS.
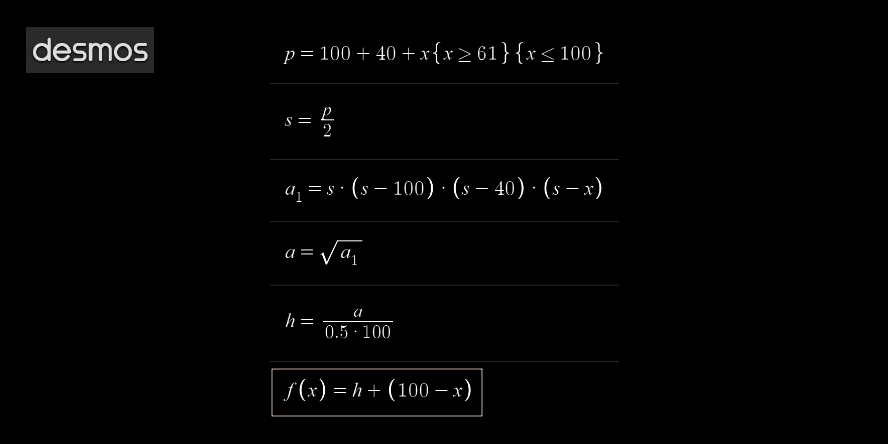

III. Résultat final:
La distance maximum entre la poutre et le poids est de 51,904 cm (la corde entre B et C mesurant alors 71,322 cm).