une
histoire
de
bougies
histoire
de
bougies
(avec la contribution de Laurent M.)

PROBLÈME
1. Description:
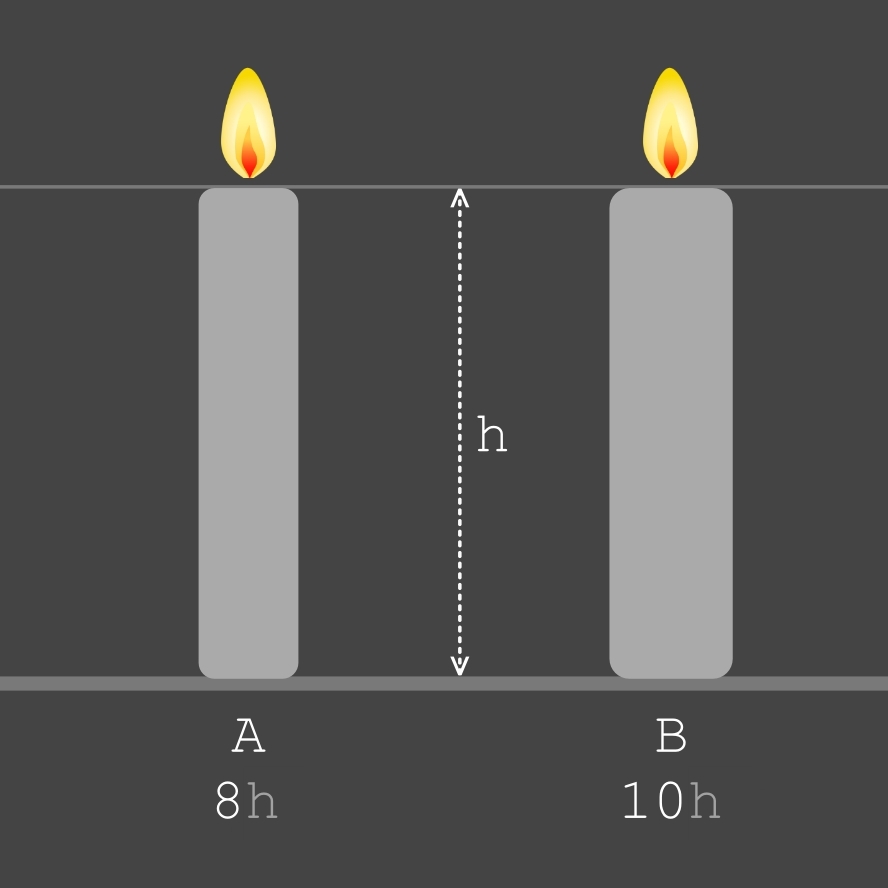
Deux bougies de même hauteur mais d'épaisseur différente sont allumées en même temps.
La première bougie (A) brûlera complètement en 8 heures et la deuxième bougie (B) brûlera complètement en 10 heures.
La première bougie (A) brûlera complètement en 8 heures et la deuxième bougie (B) brûlera complètement en 10 heures.
2. Question:
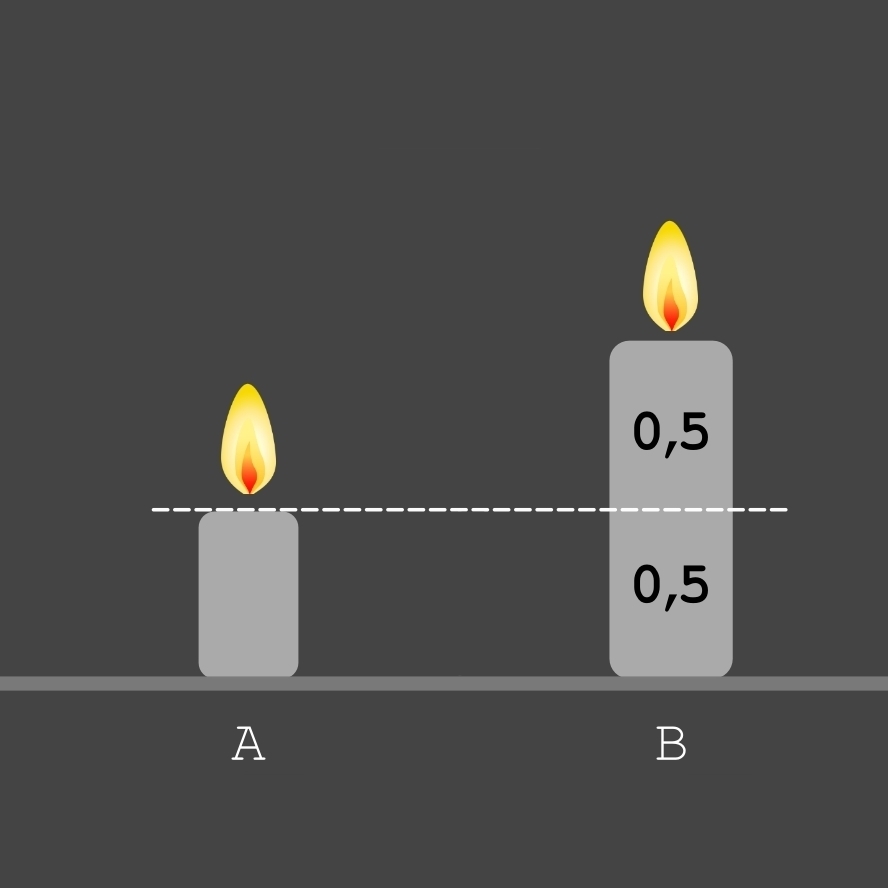
Au bout de combien de temps la hauteur de la bougie A sera égale à la moitié de la hauteur de la bougie B ?
Bien, bien ...
Mais par où commencer ?
SOLUTION
3. Étudier le problème:
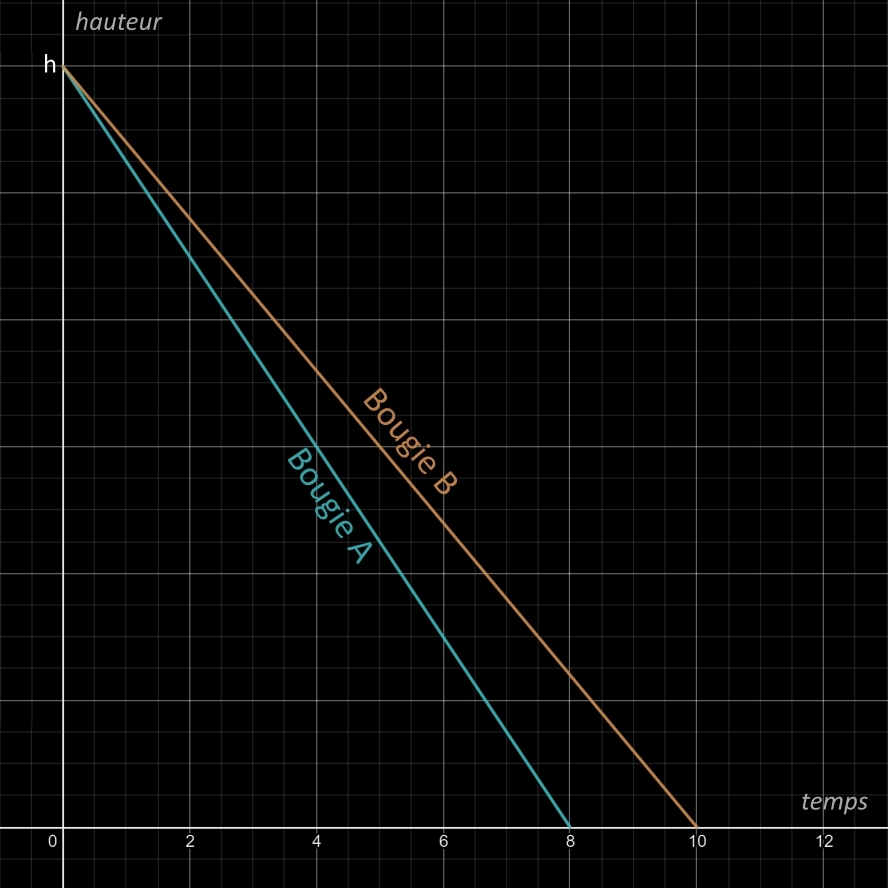
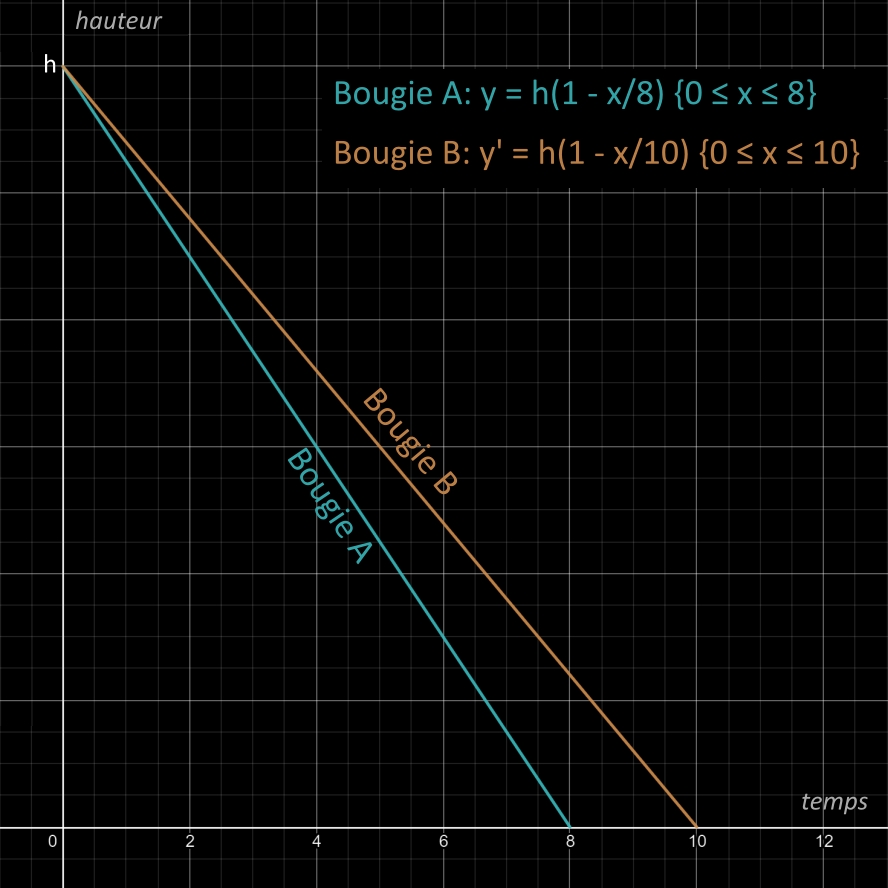
En partant de la hauteur h (hauteur initiale) jusqu'à la consumation totale des deux bougies sur une échelle du temps (8 heures pour la bougie A et 10 heures pour la bougie B)
une représentation par deux équations de droite semble être un bon moyen pour observer la progression de la consumation des deux bougies.
4. Déterminer les équations des 2 droites:
Rappel: une fonction de droite est du type:
• y = ax + b
• a = pente de la droite
• b = ordonnée à l'origine
---=O=---
Calcul de la fonction de la bougie A:
• a = -h/temps(A) (*)
• a = -h/8 (*)
(*) la pente est négative car h diminue avec le temps
• b = h
• y = -(h/8)x + h
• y = h(-x/8 + 1)
• y = h(1 - x/8)
Ajout du domaine de la fonction:
• x est compris entre 0 et 8 (bornes incluses)
• donc y = h(1 - x/8) {0 ≤ x ≤ 8}
---=O=---
Calcul de la fonction de la bougie B:
• raisonnement identique à celui de la bougie A
• temps(B) = 10
• on obtient donc: y' = h(1 - x/10) {0 ≤ x ≤ 10}
• y = ax + b
• a = pente de la droite
• b = ordonnée à l'origine
---=O=---
Calcul de la fonction de la bougie A:
• a = -h/temps(A) (*)
• a = -h/8 (*)
(*) la pente est négative car h diminue avec le temps
• b = h
• y = -(h/8)x + h
• y = h(-x/8 + 1)
• y = h(1 - x/8)
Ajout du domaine de la fonction:
• x est compris entre 0 et 8 (bornes incluses)
• donc y = h(1 - x/8) {0 ≤ x ≤ 8}
---=O=---
Calcul de la fonction de la bougie B:
• raisonnement identique à celui de la bougie A
• temps(B) = 10
• on obtient donc: y' = h(1 - x/10) {0 ≤ x ≤ 10}
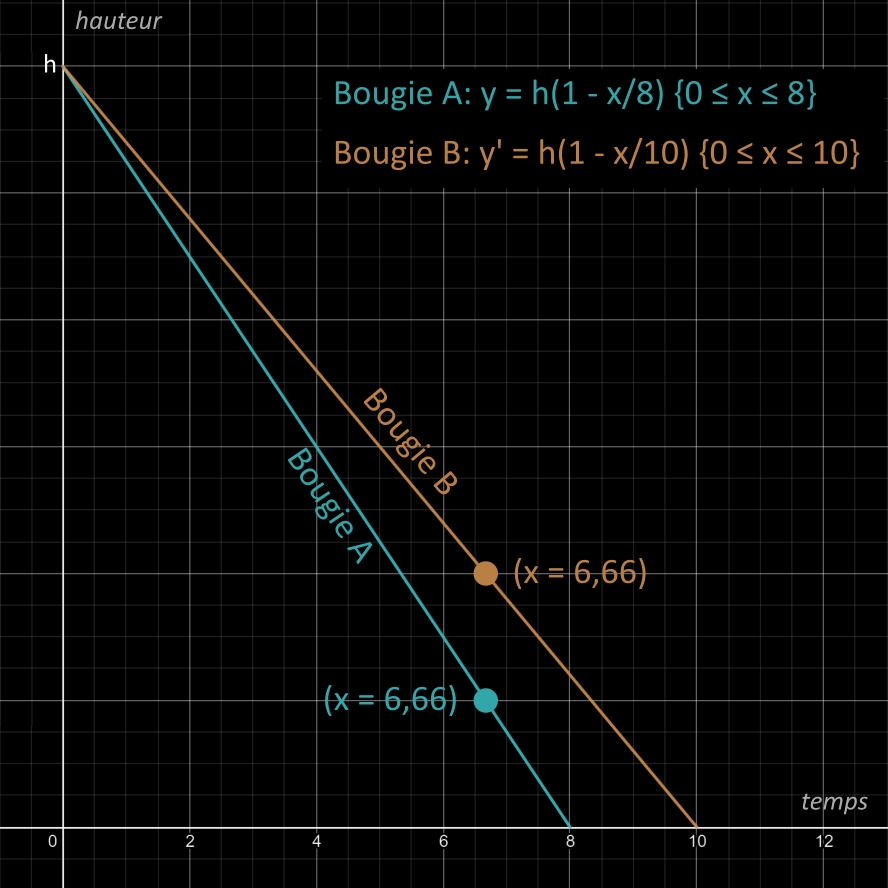
5. Trouver le résultat du problème:
La question était (rappel):
Au bout de combien de temps la hauteur de la bougie A sera égale à la moitié de la hauteur de la bougie B ?
---=O=---
La réponse sera:
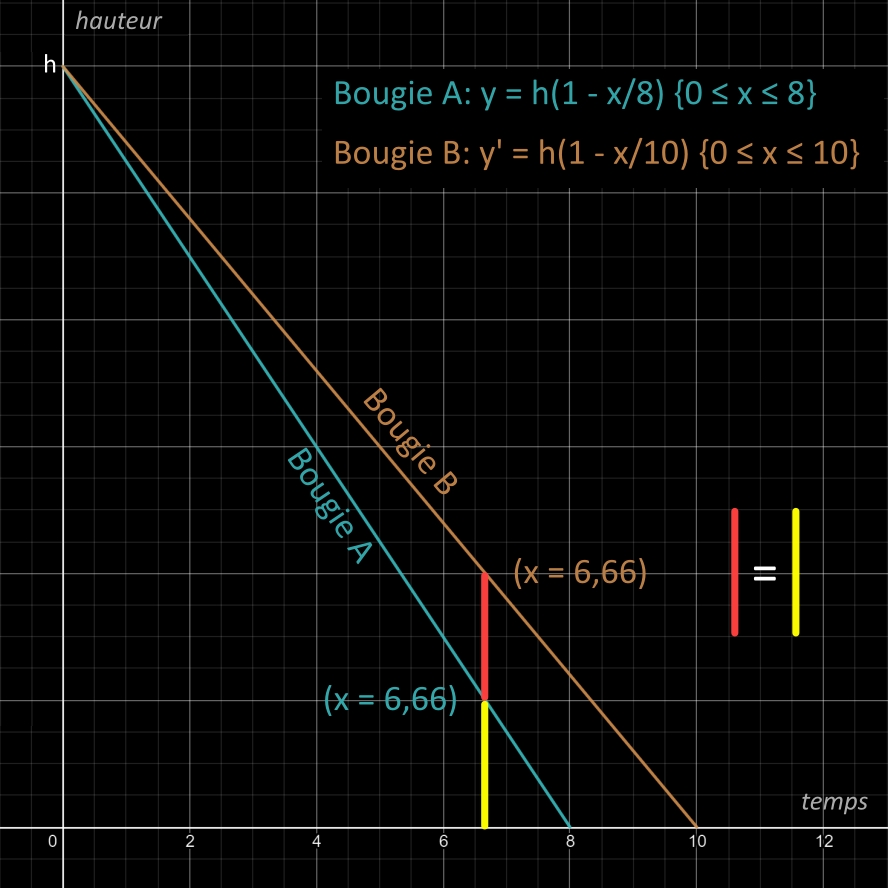
• que vaudra x quand y' vaudra 2y ?
• soit y' = 2y
et comme:
• y = h(1 - x/8)
• y' = h(1 - x/12)
on obtient alors:
• h(1 - x/10) = 2h(1 - x/8)
---=O=---
Calcul de x:
• on divise les 2 termes par h
• (1 - x/10) = 2(1 - x/8)
• et on poursuit le calcul
• 1 - x/10 = 2 - 2x/8
• 1 - x/10 = 2 - x/4
• 1 - 2 = x/10 - x/4
• -1 = 2x/20 - 5x/20
• -1 = -3x/20
• -20 = -3x
• x = -20/-3
• x = 6,66
---=O=---
Conversion mode décimal en mode horaire:
• 6,66 = 6 + 2/3
• 2/3 de 60 mn = 40 mn
• donc 6,66 =
Au bout de combien de temps la hauteur de la bougie A sera égale à la moitié de la hauteur de la bougie B ?
---=O=---
La réponse sera:
• que vaudra x quand y' vaudra 2y ?
• soit y' = 2y
et comme:
• y = h(1 - x/8)
• y' = h(1 - x/12)
on obtient alors:
• h(1 - x/10) = 2h(1 - x/8)
---=O=---
Calcul de x:
• on divise les 2 termes par h
• (1 - x/10) = 2(1 - x/8)
• et on poursuit le calcul
• 1 - x/10 = 2 - 2x/8
• 1 - x/10 = 2 - x/4
• 1 - 2 = x/10 - x/4
• -1 = 2x/20 - 5x/20
• -1 = -3x/20
• -20 = -3x
• x = -20/-3
• x = 6,66
---=O=---
Conversion mode décimal en mode horaire:
• 6,66 = 6 + 2/3
• 2/3 de 60 mn = 40 mn
• donc 6,66 =
6 heures et 40 minutes

problème
proposé sur
chaîne YouTube
MindYourDecisions
