une
question
(ouverte)
concernant
les médiatrices
dans un triangle
question
(ouverte)
concernant
les médiatrices
dans un triangle

RAPPEL
Définition
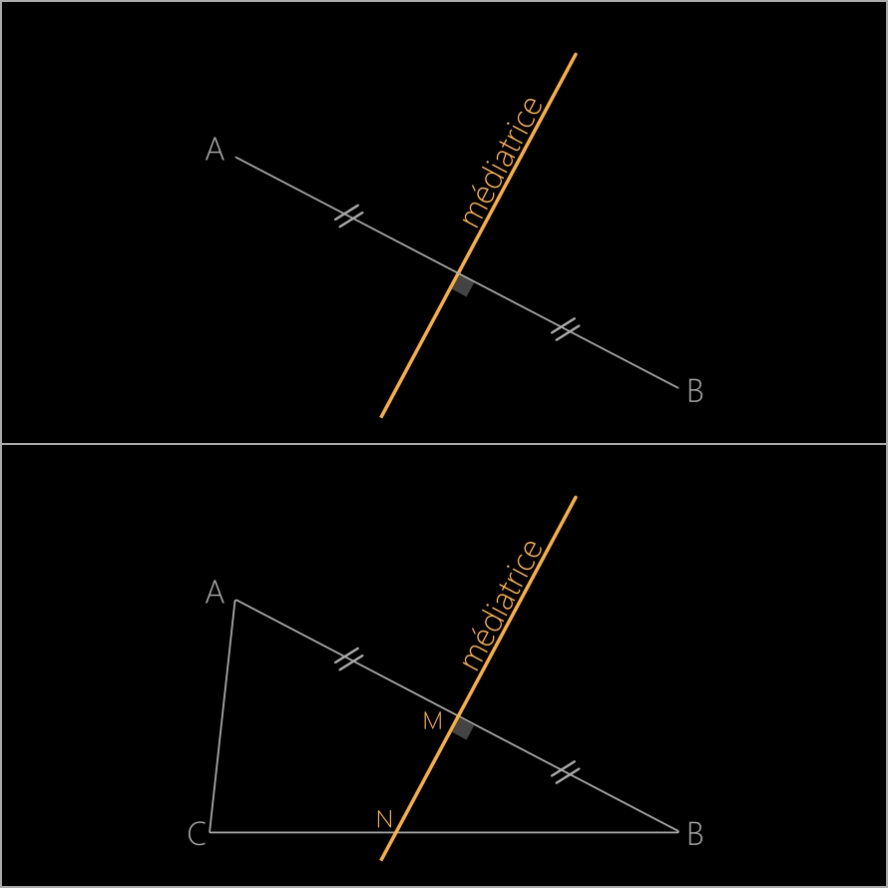
La médiatrice d'un segment (AB ci-dessous) est la droite qui coupe perpendiculairement ce segment en son milieu.
La médiatrice du côté AB du triangle ABC (ci-dessous) coupe AB en M et BC en N.
Pour calculer la longueur de MN il faut appliquer une formule.
Cette formule est la finalité principale de cette page.
La médiatrice du côté AB du triangle ABC (ci-dessous) coupe AB en M et BC en N.
Pour calculer la longueur de MN il faut appliquer une formule.
Cette formule est la finalité principale de cette page.

LA FORMULE
Exemple
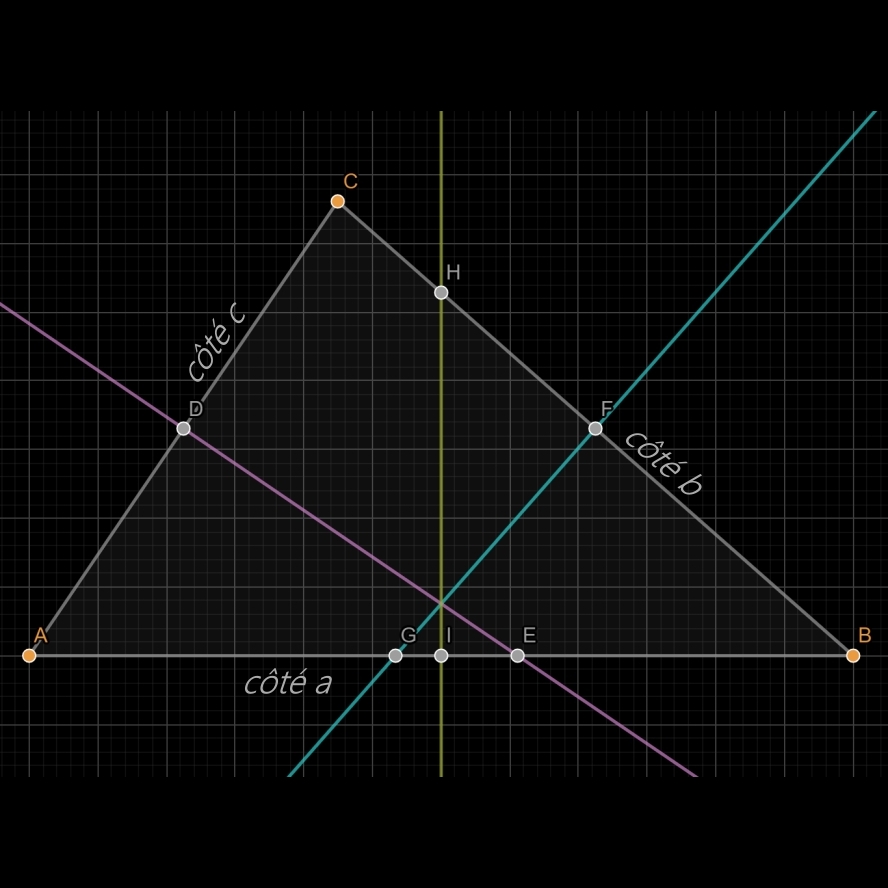
Soit le triangle (quelconque) ABC ci-dessous sur lequel apparaissent les 3 médiatrices:
• en jaune (IH) la médiatrice du côté a (AB)
• en cyan (FG) la médiatrice du côté b (BC)
• en rose (DE) la médiatrice du côté c (AC)
• en jaune (IH) la médiatrice du côté a (AB)
• en cyan (FG) la médiatrice du côté b (BC)
• en rose (DE) la médiatrice du côté c (AC)
La formule
Pour appliquer la formule, il faut 3 préalables:
1) connaître la longueur de chaque côté:
• côté a (AB) = 12
• côté b (BC) = 10
• côté c (AC) = 8
2) connaître l'aire du triangle:
• S = surface (aire) = 39,69
3) ordonner, du plus grand au plus petit, les 3 côtés:
• on obtiendra: a ≥ b ≥ c
• note: cet ordonnancement est très important !
1) connaître la longueur de chaque côté:
• côté a (AB) = 12
• côté b (BC) = 10
• côté c (AC) = 8
2) connaître l'aire du triangle:
• S = surface (aire) = 39,69
3) ordonner, du plus grand au plus petit, les 3 côtés:
• on obtiendra: a ≥ b ≥ c
• note: cet ordonnancement est très important !

Application de la formule
Résultats attendus:
• longueur mesurée de la médiatrice IH = 5,29
• longueur mesurée de la médiatrice FG = 4,41
• longueur mesurée de la médiatrice DE = 5,88
Résultats calculés (avec la formule):
• voir ci-dessous
• longueur mesurée de la médiatrice IH = 5,29
• longueur mesurée de la médiatrice FG = 4,41
• longueur mesurée de la médiatrice DE = 5,88
Résultats calculés (avec la formule):
• voir ci-dessous


QUESTION
Question ouverte
La formule fonctionne parfaitement pour n'importe quel triangle (quelconque, rectangle, isocèle ou équilatéral).
Elle fonctionne également parfaitement avec un triangle comprenant des angles obtus et même si deux médiatrices en venaient alors à couper le même côté opposé.
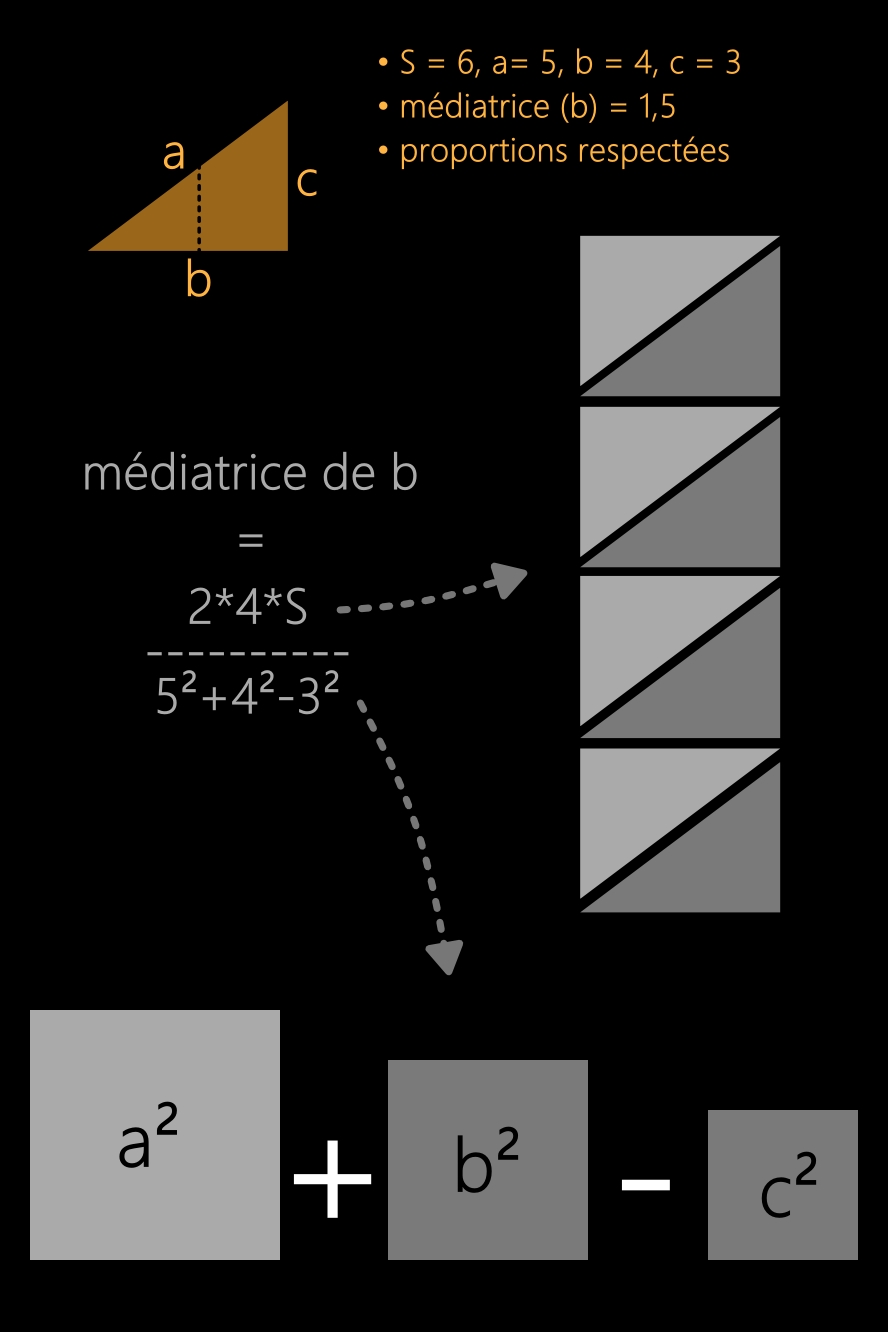
Comment comprendre le fonctionnement de cette formule (surfaces manipulées et divisées entre elles) ?
Ci-dessous, en respectant les proportions, voici une "matérialisation" du contenu du numérateur et du dénominateur de la formule à partir d'un triangle rectangle (de côtés 3,4 et 5).
Autre questionnement: le numérateur de la formule change pour la médiatrice du plus petit des 3 côtés d'un triangle mais reste le même pour les 2 autres.
Elle fonctionne également parfaitement avec un triangle comprenant des angles obtus et même si deux médiatrices en venaient alors à couper le même côté opposé.
Comment comprendre le fonctionnement de cette formule (surfaces manipulées et divisées entre elles) ?
Ci-dessous, en respectant les proportions, voici une "matérialisation" du contenu du numérateur et du dénominateur de la formule à partir d'un triangle rectangle (de côtés 3,4 et 5).
Autre questionnement: le numérateur de la formule change pour la médiatrice du plus petit des 3 côtés d'un triangle mais reste le même pour les 2 autres.