divisibilité
de
la somme
ou
du produit
de
3 entiers
consécutifs
de
la somme
ou
du produit
de
3 entiers
consécutifs
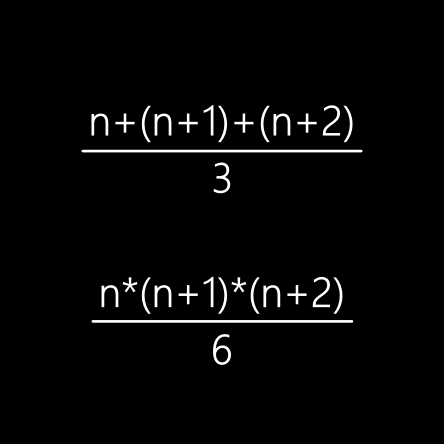

|

|

|
Somme
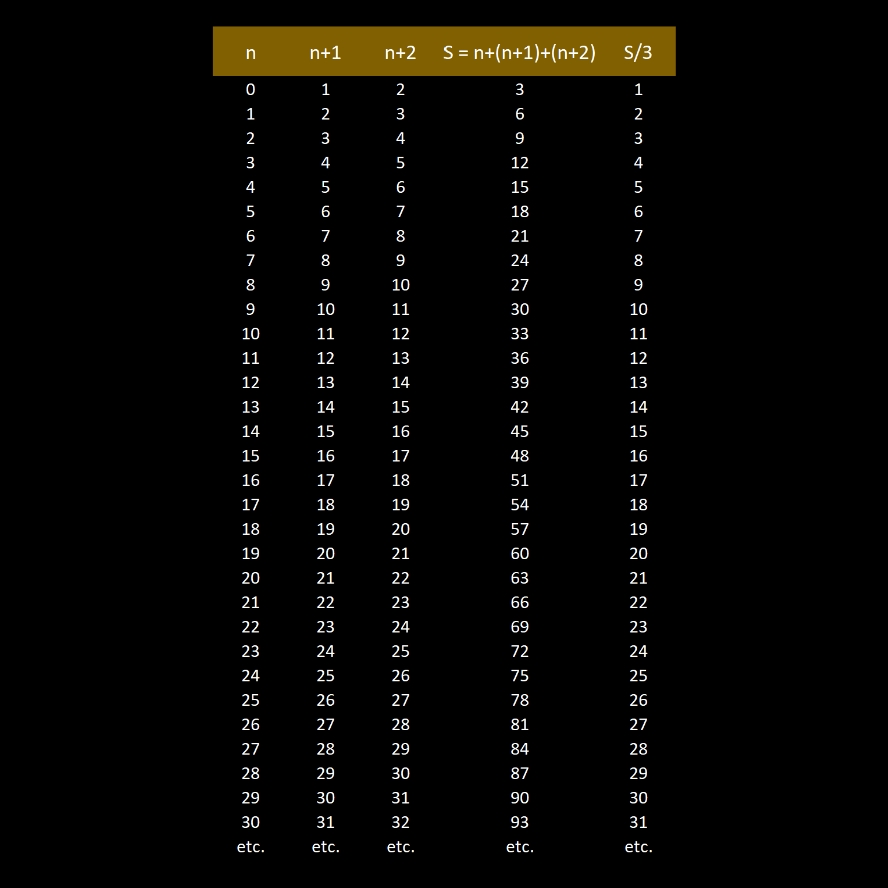
La somme de 3 entiers consécutifs:
La somme de 3 entiers consécutifs est toujours divisible par 3 (voir ci-dessous).
01
Divisibilté par 3:
• le premier entier est n
• le deuxième entier consécutif est n+1
• le troisième entier consécutif est n+2
en conséquence:
• somme = n + (n+1) + (n+2)
• somme = n + n + n + 1 + 2
• somme = 3n + 3
• somme = 3(n + 1)
Exemples:
• la somme de 306 + 307 + 308 = 3*307 = 921
• la somme de 7210 + 7211 + 7213 = 3*7211 = 21633
• le premier entier est n
• le deuxième entier consécutif est n+1
• le troisième entier consécutif est n+2
en conséquence:
• somme = n + (n+1) + (n+2)
• somme = n + n + n + 1 + 2
• somme = 3n + 3
• somme = 3(n + 1)
--=O=--
Constat: la somme de 3 nombres entiers consécutifs est toujours égale à 3 fois le nombre qui est au milieu de la série.
--=O=--
On peut également dire que pour calculer (rapidement) la somme de 3 nombres entiers consécutifs il suffit de multiplier par 3 le nombre qui est au milieu de la série.
Exemples:
• la somme de 306 + 307 + 308 = 3*307 = 921
• la somme de 7210 + 7211 + 7213 = 3*7211 = 21633

|

|

|
Produit
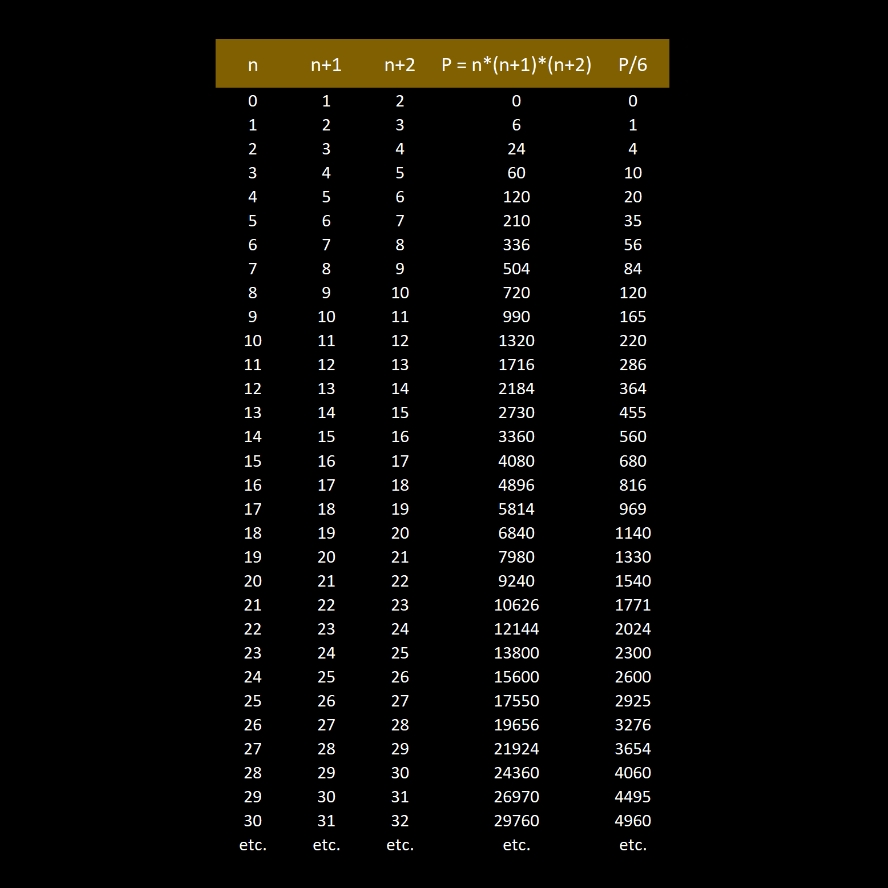
Le produit de 3 entiers consécutifs:
Le produit de 3 entiers consécutifs est toujours divisible par 6 (voir ci-dessous).
02
Rappel:
Tout nombre entier peut-être décomposé en un produit de facteurs premiers (c'est-à-dire en un produit de facteurs de nombres premiers).
Exemples:
• 6 = 2*3 (2 et 3 sont des facteurs premiers)
• 18 = 2*3*3
• 24 = 2*2*2*3
• 25 = 5*5
• 1024 = 2*2*2*2*2*2*2*2*2*2 (ou 2 puissance 10)
• 2017 = 1*2017 (car 2017 est un nombre premier)
• 2022 = 2*3*337
Dans une suite de 3 entiers consécutifs, il y a au moins un nombre entier pair (sinon deux), et un nombre pair est toujours divisible par le facteur premier 2.
Exemple:
• n = 561 = 3*11*17
• n+1 = 562 = 2*281 (562 est pair)
• n+2 = 563 = 1*563
Comme il s'agit de suites consécutives de 3 nombres entiers, chacune des suites comprendra obligatoirement un nombre appartenant la table des 3. Et ce nombre sera alors divisible par le facteur premier 3.
Exemple:
• n = 19
• n+1 = 20
• n+2 = 21 = 3*7 (21 appartient à la table des 3)
Autre exemple:
• n = 561 = 3*187 (561 appartient à la table des 3)
• n+1 = 562
• n+2 = 563
Un nombre est divisible par 6 si sa décomposition, en un produit de facteurs premiers, contient 2 et 3.
Exemples:
• 24 = 2*2*2*3 (24 est divisible par 6)
• 8*12 = (2*2*2)*(2*2*3) (8*12 est divisible par 6)
• 75 = 3*5*5 (75 n'est pas divisible par 6)
Le produit de 3 nombres entiers consécutifs est toujours divisible par 6 car la décomposition des nombres de cette suite en un produit de facteurs premiers contient le facteur 2 et le facteur 3.
Tout nombre entier peut-être décomposé en un produit de facteurs premiers (c'est-à-dire en un produit de facteurs de nombres premiers).
Exemples:
• 6 = 2*3 (2 et 3 sont des facteurs premiers)
• 18 = 2*3*3
• 24 = 2*2*2*3
• 25 = 5*5
• 1024 = 2*2*2*2*2*2*2*2*2*2 (ou 2 puissance 10)
• 2017 = 1*2017 (car 2017 est un nombre premier)
• 2022 = 2*3*337
--=O=--
Divisibilité par 2:
Dans une suite de 3 entiers consécutifs, il y a au moins un nombre entier pair (sinon deux), et un nombre pair est toujours divisible par le facteur premier 2.
Exemple:
• n = 561 = 3*11*17
• n+1 = 562 = 2*281 (562 est pair)
• n+2 = 563 = 1*563
--=O=--
Divisibilité par 3:
Comme il s'agit de suites consécutives de 3 nombres entiers, chacune des suites comprendra obligatoirement un nombre appartenant la table des 3. Et ce nombre sera alors divisible par le facteur premier 3.
Exemple:
• n = 19
• n+1 = 20
• n+2 = 21 = 3*7 (21 appartient à la table des 3)
Autre exemple:
• n = 561 = 3*187 (561 appartient à la table des 3)
• n+1 = 562
• n+2 = 563
--=O=--
Divisibilité par 6:
Un nombre est divisible par 6 si sa décomposition, en un produit de facteurs premiers, contient 2 et 3.
Exemples:
• 24 = 2*2*2*3 (24 est divisible par 6)
• 8*12 = (2*2*2)*(2*2*3) (8*12 est divisible par 6)
• 75 = 3*5*5 (75 n'est pas divisible par 6)
Le produit de 3 nombres entiers consécutifs est toujours divisible par 6 car la décomposition des nombres de cette suite en un produit de facteurs premiers contient le facteur 2 et le facteur 3.

|

|

|
