é
n
i
g
m
e
avec
trois
rectangles
n
i
g
m
e
avec
trois
rectangles


|

|

|
Note: dans sa résolution, cette énigme aborde la congruence de figures géométriques c'est-à-dire la relation par laquelle deux figures
peuvent être amenées à coïncider parfaitement l’une sur l’autre par une isométrie (même mesure) directe.

|

|

|
I. La question

01
Soit trois rectangles identiques: deux en rouge et un en vert.

02
Les trois rectangles sont disposés selon le dessin ci-dessus ...

03
... avec les rectangles rouges par-faitement alignés.
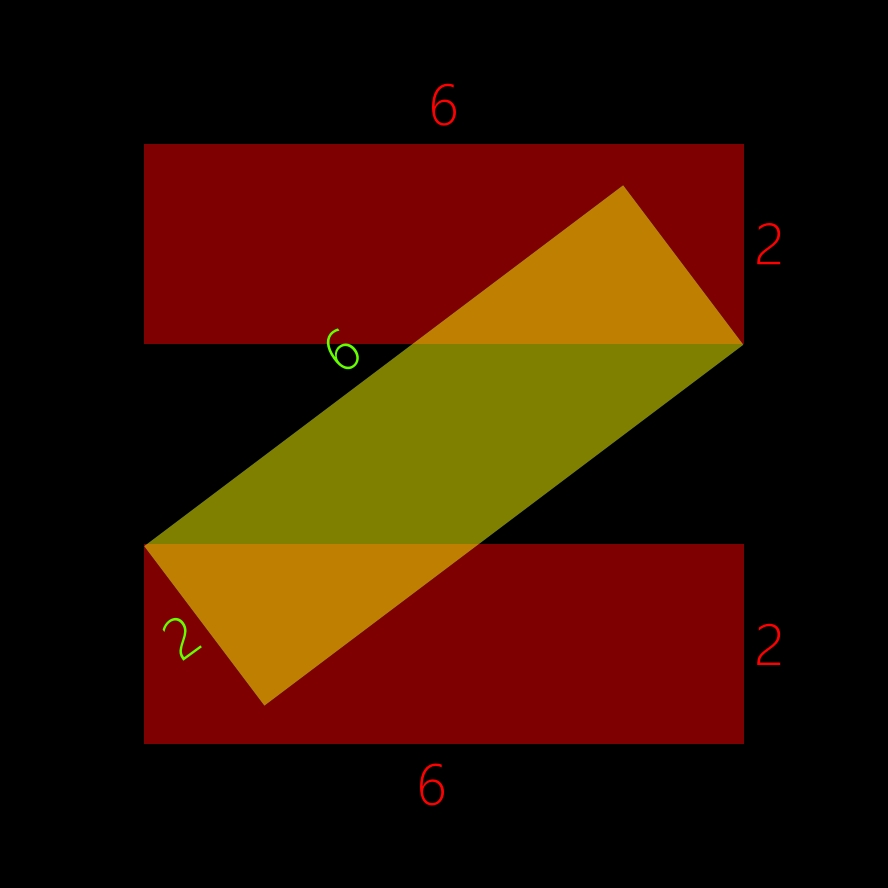
04
Chaque rectangle mesure 6 unités de longueur sur 2 unités de largeur.
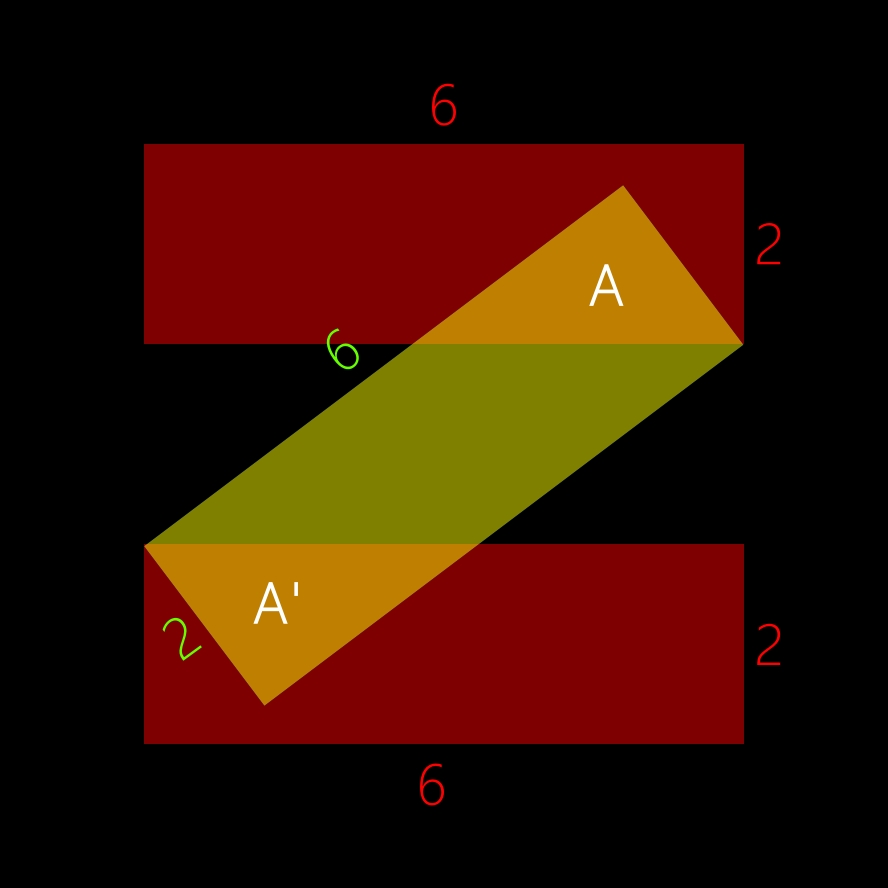
05
Que valent les aires des triangles (de couleur jaune) A et A' ?

|

|

|
II. La réponse
(point par point et illustrée d'images)
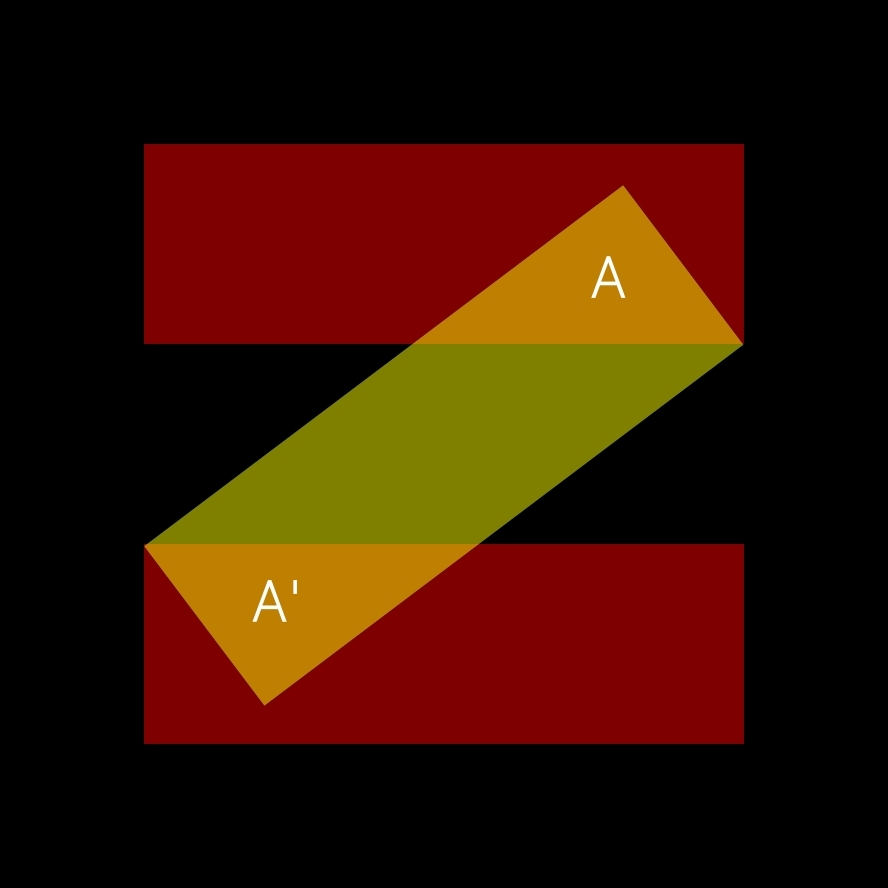
06
On note que, dans la symétrie de l'ensemble de la figure des trois rectangles, les triangles A et A' sont égaux.
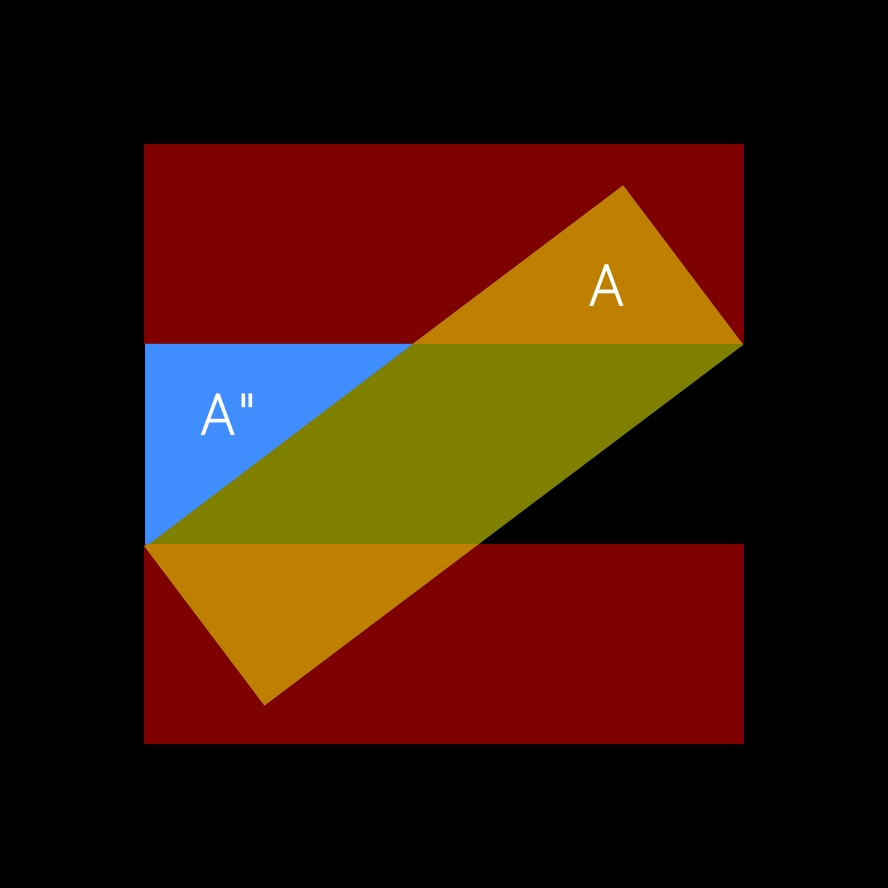
07
Il faut démontrer que les triangles A et A" sont égaux.
08
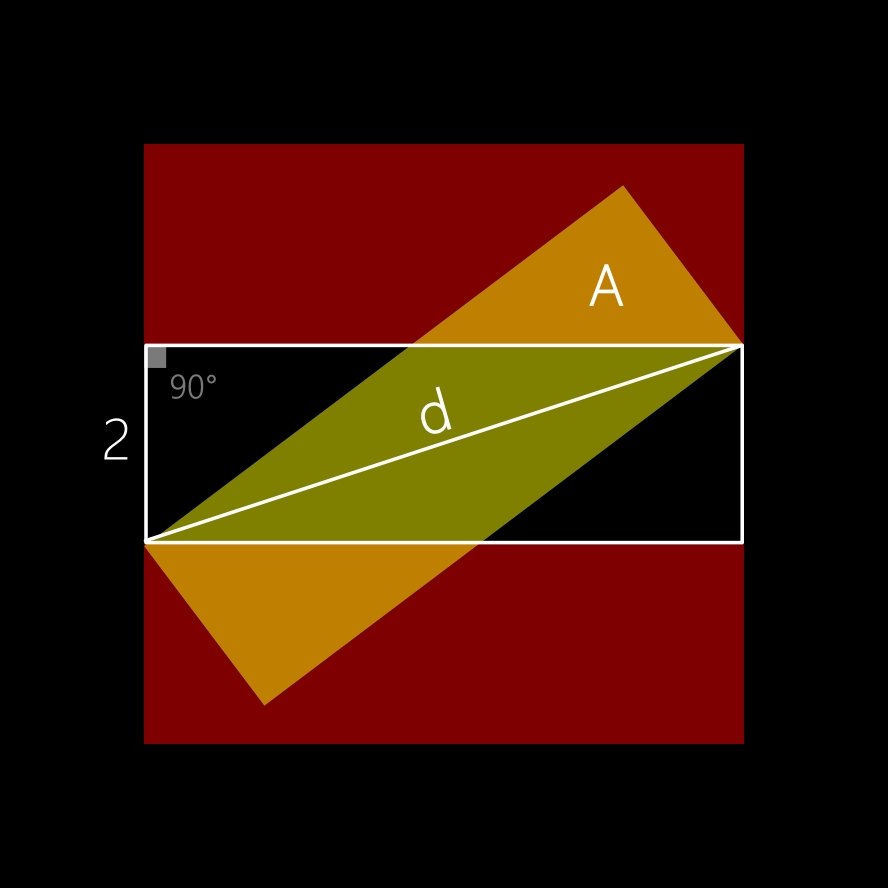
L'espace entre les rectangles rouges est un rectangle car les rectangles rouges sont alignés (hypothèse de départ).
La longueur du rectangle entre les deux rectangles rouges est 6 (hypothèse de départ).
La diagonale d est la même que celle du rectangle (oblique) vert.
Les deux rectangles ayant un côté de même longueur (6) et la diagonale également de même longueur, ils sont donc égaux (règles de la congruence géométrique).
Il en découle que la largeur du rectangle entre les rectangles rouges est 2.
09
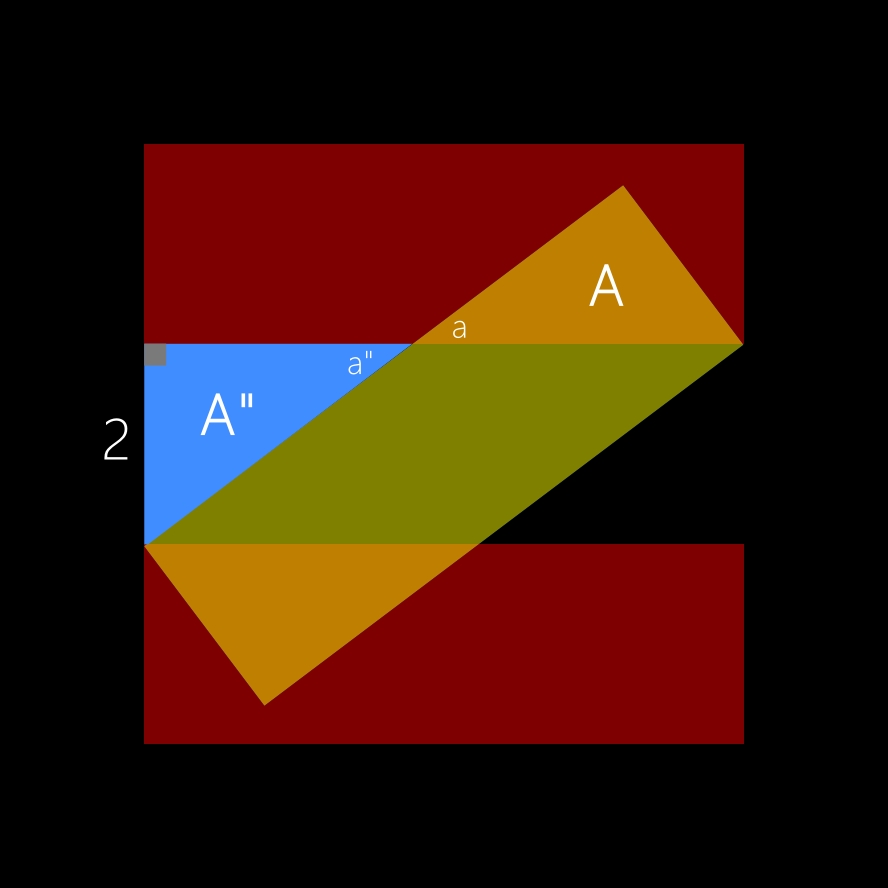
On sait que le triangle A" possède un côté égal à 2.
Si deux angles sont opposés par le sommet, alors ils sont égaux. En conséquence, les angles a et a" sont égaux.
Les deux triangles ayant deux angles de même valeur (l'angle droit et les angles a et a") et un côté de même longueur (2), ils sont donc égaux (règles de la congruence géométrique).
10
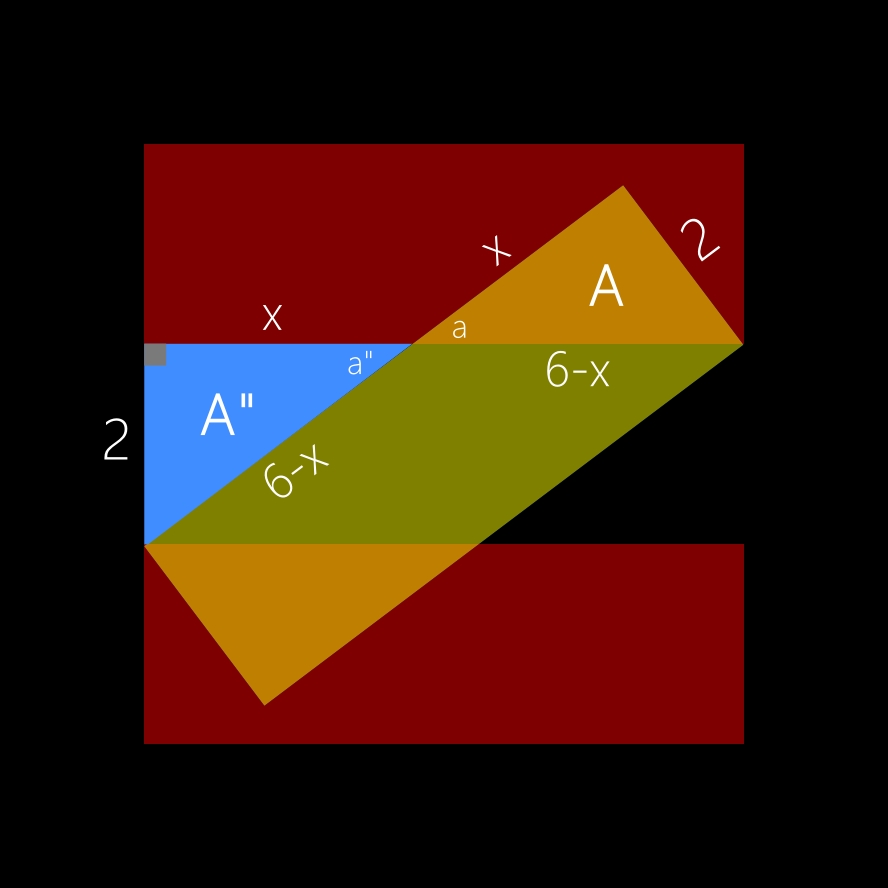
On peut donc calculer l'aire de A.
1) Théorème de Pythagore:
• x²+2² = (6-x)²
• x²+4 = 36-12x+x²
• x²-x²+12x = 36-4
• 12x = 32
• x = 32/12 = 8/3
2) Calcul de l'aire du triangle:
• aire = (hauteur * base) / 2
• hauteur = 2
• base = x
• aire(A) = (x*2)/2 = ((8/3)*2)/2 = 8/3
• triangle A = triangle A'
• aire(A') = 8/3
3) Conclusion:
aire(A) + aire(A') = 16/3

|

|

|
