r
é
s
o
l
u
t
i
o
n
s
de
quelques
exercices
mathématiques
é
s
o
l
u
t
i
o
n
s
de
quelques
exercices
mathématiques

Apprendre par l'exemple.
Le but de cette page est de découvrir, à travers des exercices, les outils, les stratagèmes et les astuces mathématiques mis en oeuvre pour la résolution des problèmes proposés.
Pour chaque exercice, un lien permet de visualiser la résolution enregistrée dans un fichier PDF qui est accessible sans mot de passe en cliquant sur les yeux (•_•) de l'exercice correspondant.
Il y a 24 exercices (le 15/08/2023).

résoudre l'équation exponentielle
ci-dessous
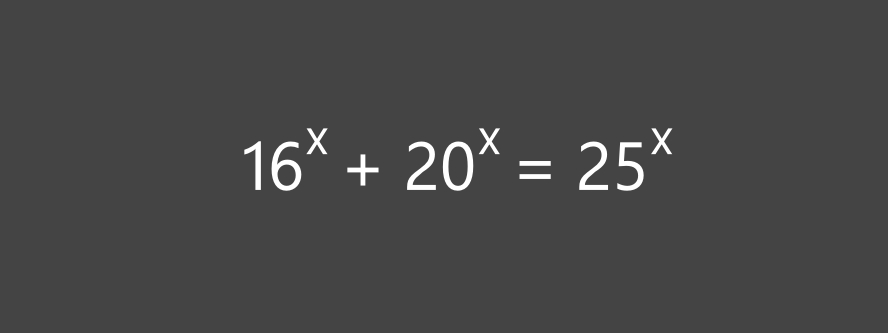
• voir (PDF) ... (•_•)

résoudre l'équation
ci-dessous
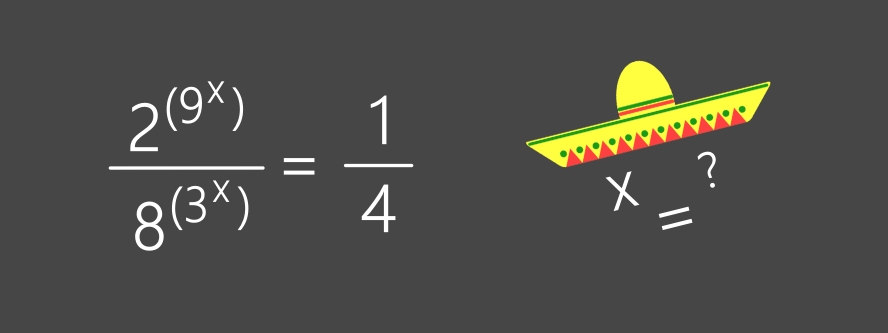
• voir (PDF) ... (•_•)

résoudre le problème
ci-dessous

• voir (PDF) ... (•_•)

factoriser au maximum
l'expression ci-dessous
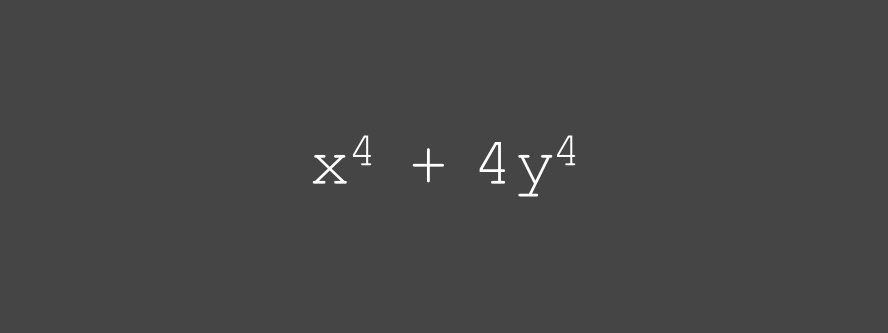
• voir (PDF) ... (•_•)

résoudre
le système d'équations
présenté ci-dessous

• voir (PDF) ... (•_•)

soit m et n les racines de
l'équation présentée ci-dessous,
que vaut m^4 + n^4 ?
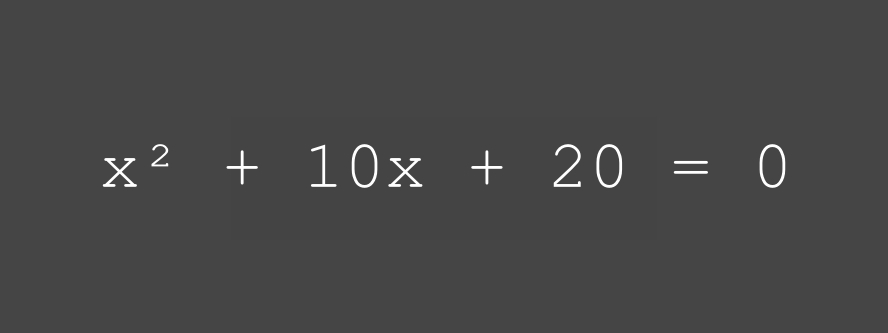
• voir (PDF) ... (•_•)

trouver
la valeur recherchée
dans le système ci-dessous
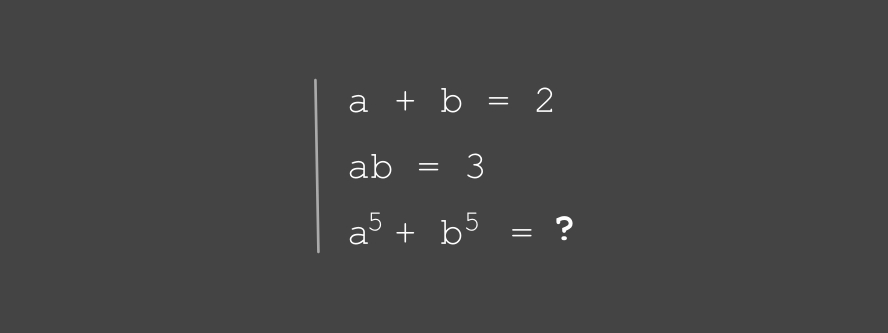
La réponse comprend un bonus.
• voir (PDF) ... (•_•)

à partir d'une égalité,
calculer ... (voir ci-dessous)
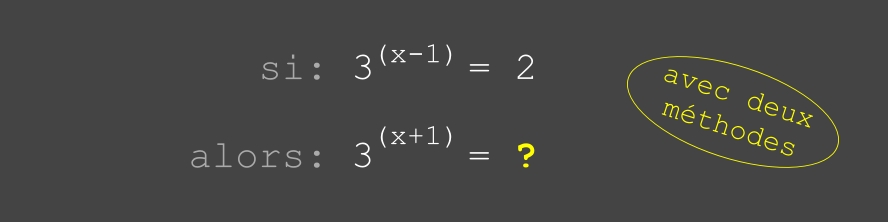
• voir (PDF) ... (•_•)

résoudre le système
d'équations (ci-dessous)
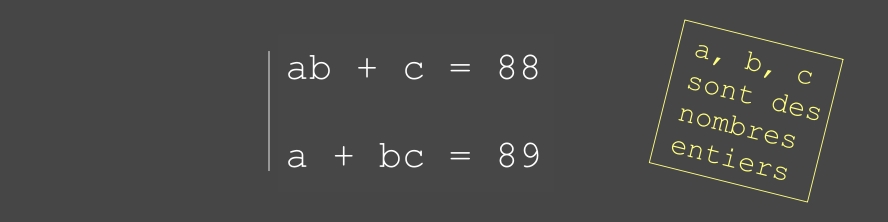
• voir (PDF) ... (•_•)

calculer la longueur
de la médiatrice MN
dans la figure ci-dessous
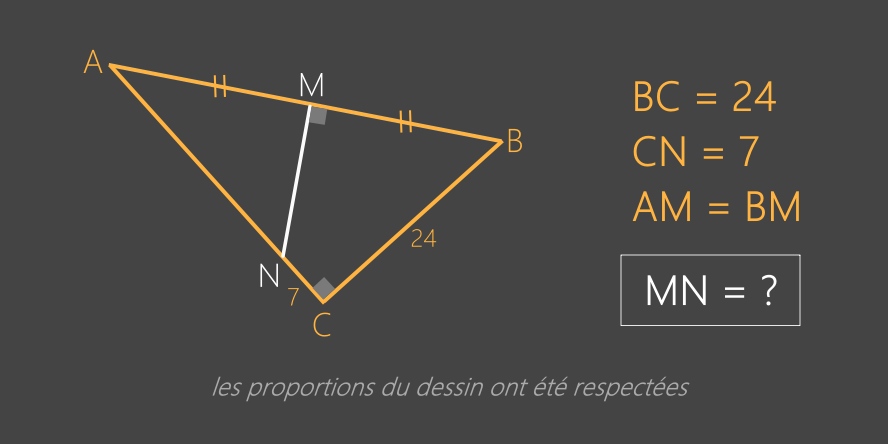
Note: le PDF bonus contient la forme géométrique finale avec toutes les cotes calculées.
Bonus réalisé avec l'outil en ligne (gratuit) GeoGebra qui permet de faire de la géométrie dynamique en 2D/3D.
Bonus réalisé avec l'outil en ligne (gratuit) GeoGebra qui permet de faire de la géométrie dynamique en 2D/3D.

calculer 2 des longueurs
d'un
triangle rectangle
connaissant
aire et hypoténuse

Note: on peut même en déduire une formule générale.
• voir (PDF) ... (•_•)

résoudre le système
d'équations (ci-dessous)
en utilisant la
méthode du pivot de GAUSS
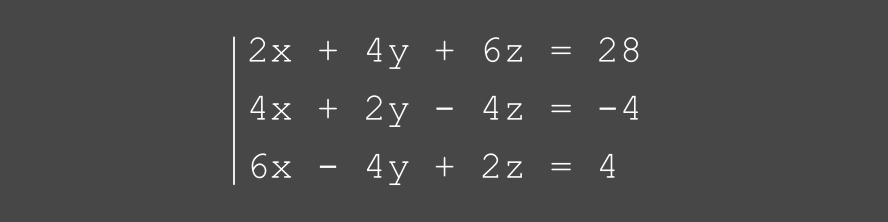
Note: la méthode du pivot de Gauss est une méthode pour transformer un système en un autre système qui est "triangulaire" et donc facile à résoudre.
• voir (PDF) ... (•_•)

résoudre le système
d'équations (ci-dessous)
en utilisant les MATRICES
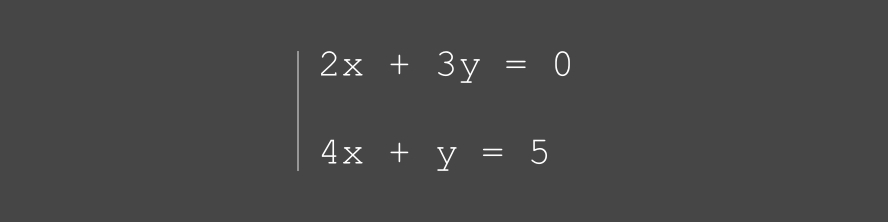
Note: la solution très détaillée de cet exercice inclut des éléments de base nécessaires à l'appréhension des matrices.
• voir (PDF) ... (•_•)

trouver la valeur de x dans
l'expression ci-dessous
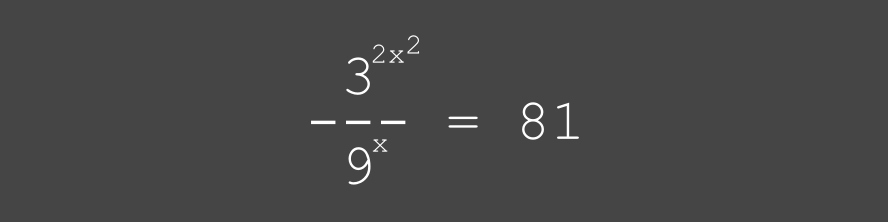
• voir (PDF) ... (•_•)

factoriser l'expression
ci-dessous afin de pouvoir
attribuer mentalement des
valeurs à x et à y
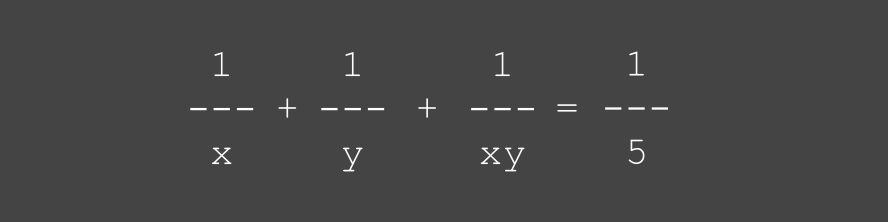
• voir (PDF) ... (•_•)

calculer
l'expression ci-dessous
(3 méthodes proposées)
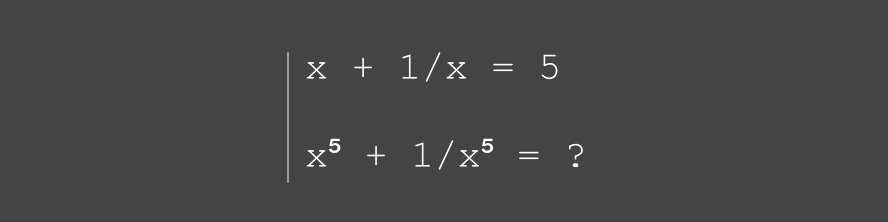
• voir (PDF) ... (•_•)

exercice de démonstration
(voir ci-dessous)
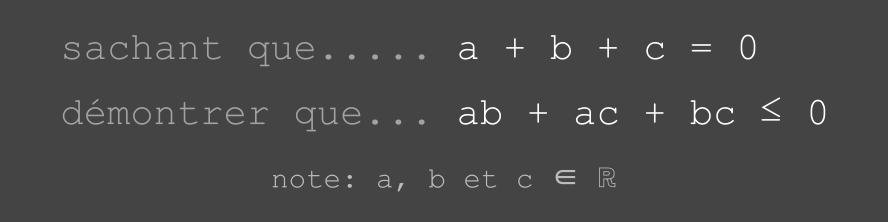
• voir (PDF) ... (•_•)

trouver 2 nombres
connaissant seulement
leur somme et leur produit
avec au moins 2 méthodes
(voir ci-dessous)

• voir (PDF) ... (•_•)

résoudre sans calculatrice
l'expression ci-dessous
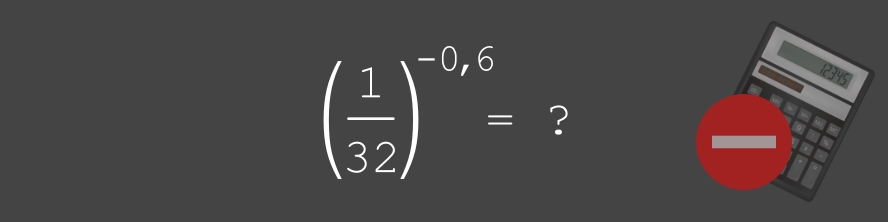
• voir (PDF) ... (•_•)

calculer l'expression
ci-dessous

• voir (PDF) ... (•_•)

calculer
sans calculatrice
la valeur décimale de:
41
-----------
2^4 * 5^3
• voir (PDF) ... (•_•)

résoudre l'équation
ci-dessous
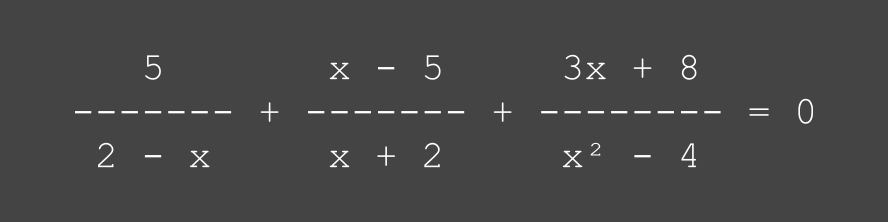
Note: l'exercice consiste à ramener l'équation à un trinôme du second degré et à définir le (ou les) valeur(s) de x selon deux méthodes:
a) par le discriminant
b) par factorisation
a) par le discriminant
b) par factorisation
• voir (PDF) ... (•_•)

calculer x dans
3^(3-x)+3^(2x-4)-18 = 0
• voir (PDF) ... (•_•)

factoriser
2xy-4y-x+2
• voir (PDF) ... (•_•)

(à suivre)
